Abstract

Animals and insects use whiskers and antennae for orientation, foraging, stalking prey, finding mates, and fighting. This article explores the function of whiskers and antennae in different environments and species. Rats use a whisking motion to contact surfaces and gather sensory information regarding object shapes and textures. Kinetic motion generated from stick-and-slip events occurring during texture discrimination appears to encode neuronal spiking. In other scenarios, rats use their whisker’s bending and vibrational magnitude in the presence of airflow to encode such a stimulus. Harbor seals can follow prey while swimming using undulated whiskers that minimize self-induced noise. Two mechanisms of interaction between whiskers and wake vortices are slip-and-stick and slaloming. Insect antenna undergoes deformation to evaluate various environmental chemical and physical properties. The inflation and contraction of the antenna are controlled by the increasing or decreasing blood pressure pumping from the antennal pulsatile organ, where the stress and strains of the antenna can be analyzed under two distinct scenarios. Despite both using antennae for hearing, the auditory systems of mosquitoes and Drosophila are not entirely the same. Here, the physical models for antennal hearing of Drosophila and mosquitoes are compared with energy expenditure and purpose.

Introduction

While humans rely on sight, touch, and hearing for guidance, insects and animals have a sixth sense that allows them to orient themselves: their whiskers and antennae. Nocturnal animals like rats that live underground evolved the ability of active sensing through whiskers, allowing them to perceive and interpret the surrounding environment without sunlight and eyesight. Similarly, harbor seals hunting in dark water rely heavily on their whiskers to track the exact path of their prey. Insects have also developed appendages that hold similar functions to those of mammal whiskers. This powerful appendage, the antenna, functions as a complex sensory organ that serves tactile, olfactory and hearing functions. Whiskers and antennae primarily provide sensory functions for creatures living in distinct environments, and variance has been discovered in the mechanism and purpose behind the application of these organs. The analysis of organisms’ effective integration of whiskers and antennae shows that these sensory organs possess ingenious physical properties and crucial evolutionary advantages.

Whiskers on Land – Rats

Rat whiskers are an essential component of their sensory system, allowing them to perceive and navigate the world around them, especially in dark and small environments. Whiskers, also known as macrovibrissae and microvibrissae depending on their size, are arranged in very specific patterns all over the rat’s body. Their length ranges anywhere from 1 to 6 cm (Yu et al., 2016). Some of the most important whiskers are found near the face of the animal, as they are involved in the process of active sensing. Two distributions of 30 conical-shaped whiskers of varying sizes are found on either side of the face (Wolfe, 2008). Rats typically gather information from their whiskers through their response to airflow or an active sensing process called whisking. Both involve very different movements and integration of physical factors to create accurate sensory responses to the state of a rat’s surroundings. While the response of vibrissae to airflow provides information on the direction and speed of this said flow, whisking allows for texture discrimination and object recognition.

Texture discrimination and object recognition through whisking

Whisking is a periodic motion of whiskers generated by intrinsic muscles controlling the movement of singular whiskers (Sofroniew & Svoboda, 2015). It is also referred to as active sensing, where rats initiate this motion to accomplish tasks or proactively gather information regarding their surroundings. The amplitude and speed of whisking can vary as a rat explores its environment (Sofroniew & Svoboda, 2015). Whisking is characterized by short sweeps of the whiskers with frequencies between 5 and 15 Hz and arcs with 25 to 75 degrees of orientations. During whisking, follicles contact surfaces in a disorderly manner, seemingly disregarding the spatial arrangement of vibrissae across a whisker pad (Diamond, 2010). 

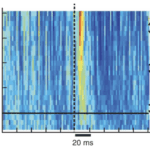
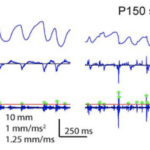
Stick and slip events are short and fast movements occurring on the surface of an object when the whisking motion of rat vibrissae contacts various textures. An average stick and slip event displaces the whisker 1.9 mm and lasts 8.6 ms (Wolfe, 2008). First, during the stick portion of the event, the tip of the whisker gets fixed in place when contacting the surface texture. This event, characterized by a whisker velocity of 0, is followed by a force applied from the shaft of the vibrissae, bending the follicle until it overcomes the force of friction and releases the whiskers in a high acceleration, high velocity motion followed by a brief oscillatory ringing. This is the slip portion of the event (Diamond, 2010). These high acceleration events set apart typical whisking in the air from whisking along solid surfaces. Figure 1 shows the increase in acceleration events in air compared to sandpaper (Wolfe, 2008).

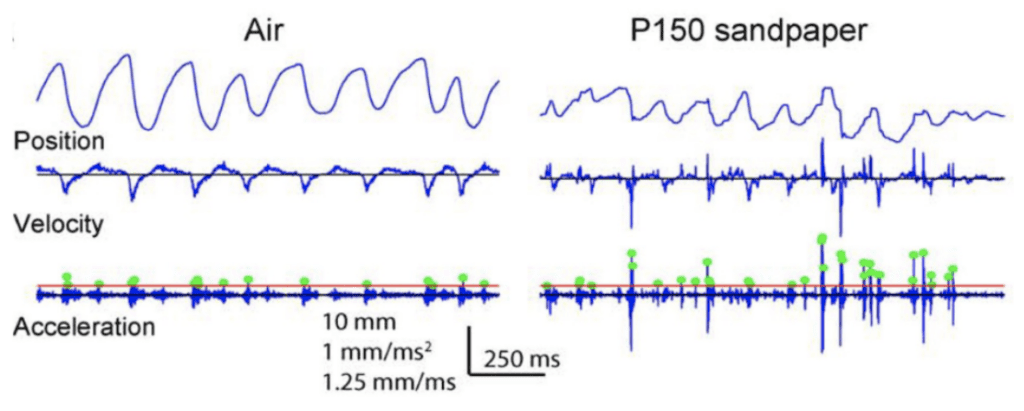
 Fig. 1 Example of the motion of the D2 whisker of rat H1 in air and on rough (P150) sandpaper. Dots indicate acceleration transients greater than 4 s.d. above mean acceleration in air (red line) (Wolfe, 2008).

Stick and slip events change multiple characteristics of whisker movement. Understanding the relationship between the state of these characteristics and neuronal encoding can be challenging as it remains unclear which aspects of whisker movement are used to gain sensory information. Two main hypotheses have been investigated to understand the sensory experience of rats based on the information provided by surface whisking.

Resonance hypothesis

This first hypothesis draws links between resonance frequency, surface texture, and whisker geometry. According to this model, as whiskers brush onto a surface, the vibration of each whisker is altered. Specific ranges of textures activate certain whiskers, as their resonance frequency is inversely proportional to the square of the length of a given vibrissae (Wolfe, 2008). In this hypothesis, the  texture is encoded through differences in vibrational amplitude caused by variations in textures. This hypothesis has been rejected since resonance magnitude has been proven to remain constant across varying textures; the resonance is independent of the surface’s roughness.

Temporal hypothesis

The second hypothesis, the one best supported by evidence, describes a correlation between the kinetic effects of sticks and slips on whiskers and texture discrimination. The high velocity and high acceleration motions of whiskers caused by periodic slips are thought to encode neuronal firing in the rat brain (Wolfe, 2008). Kinetic signatures, which can be described in terms of irregular velocity, mean speed, and composition of whisker vibrations, may be specific for different textures and describe the interaction between vibrissae and surface textures. The brain encodes those kinetic signatures to identify the surface (Wolfe, 2008). Many strings of evidence can support this hypothesis and set it apart from other models. 

First, several studies have shown that neuronal firing synchrony is increased with events of sticks and slips, generating a higher acceleration threshold (Jadhav et al., 2009). Spiking in the somatosensory cortex appears to be directly correlated to kinetic properties of whiskers following their contact with different textures. Figure 2 shows a higher firing rate of neurons 20 ms following the slip event for slip accelerations of larger magnitudes (Jadhav et al., 2009).

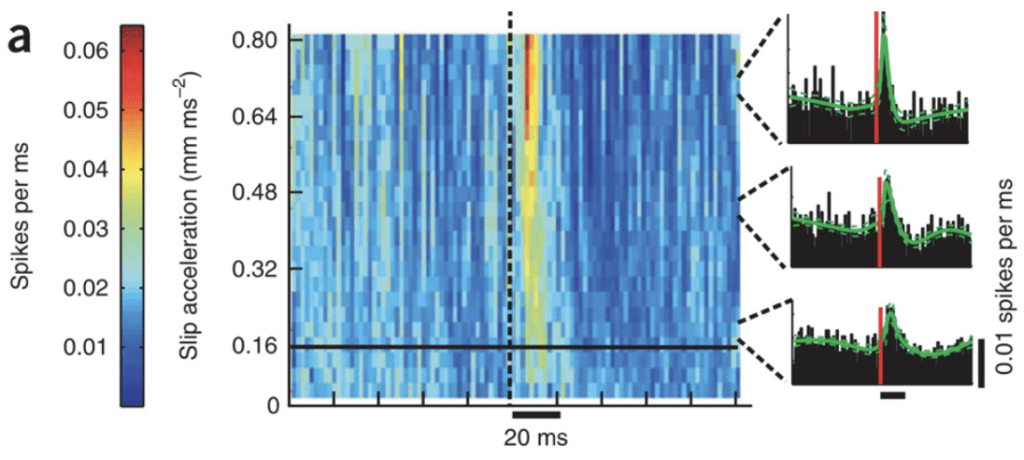
Fig. 2 Slip-acceleration response plot for an example neuron (Jadhav et al., 2009).

As the whiskers tip sticks to a given surface, the magnitude of the force necessary to overcome the force of friction will increase with coarser textures. The magnitude of the velocity and acceleration of the following slip will then be greater than the ones for smoother textures. Firing synchrony is then increased for vibrissae contact with rougher textures (Jadhav et al., 2009). 

Second, the relationship between neuronal firing rate and texture discrimination was analyzed. In this experiment, rats were trained to identify different textures. In successful trials, rougher textures encoded for an increased firing rate in the rat brain compared to smoother textures. Error trials, corresponding to 15-20 % of trials, where rats incorrectly identified the stimulus demonstrated an inverse relationship between the firing rate and surface roughness (Diamond, 2010). These experimental results further support the hypothesis linking texture discrimination to neuronal firing and kinetic state of vibrissae.  

While neuronal encoding for texture discrimination in rats is not completely understood, evidence points toward a temporal approach relating neuronal activity to the kinetic state of particular whiskers following stick-slip events. It is unlikely that rats use a singular factor to guide their perception but rather an array of physical variables to encode for sensory experience (Oladazimi, 2018).

Whisker information gathering through response to airflow

While rats use whisking and motions related to stick and slip events to encode tactile sensation, they use their vibrissae’s behavior in the presence of airflow to gather more general information regarding their surroundings. Vibrissae can respond to airflow as small as 0.5 ms^-1 enabling them to sense the flow of wind on land. During an experiment, 82 % of rats displaced either up-wind or down-wind while very few moved crosswind. The behavioral pattern observed in rats related to airflow demonstrates an ability to react to such a stimulus (Yu et al., 2016). Many factors affect the behavior of the whisker in the presence of air and impact neuronal spiking. 

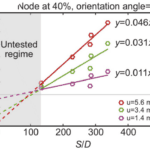
First, whiskers bend in the direction of airflow, regardless of the speed. However, the bending magnitude will vary according to the flow speed, whisker geometry as well as the orientation of the whisker relative to the air direction (Yu et al., 2016). Geometric properties of the whisker, namely, the arc length (S) and the base diameter (D), affect the bending magnitude in complex ways since whiskers do not bend as a rigid body, causing the bending magnitude to vary along their arc length (Yu et al., 2019). However, the S/D ratio, the arc length to base diameter ratio, is proportional to the bending magnitude of a whisker. Figure 3 demonstrates this approximately linear relationship for whiskers with different arc length to base diameter ratios under the effect of different airflow speeds (Yu et al., 2016).

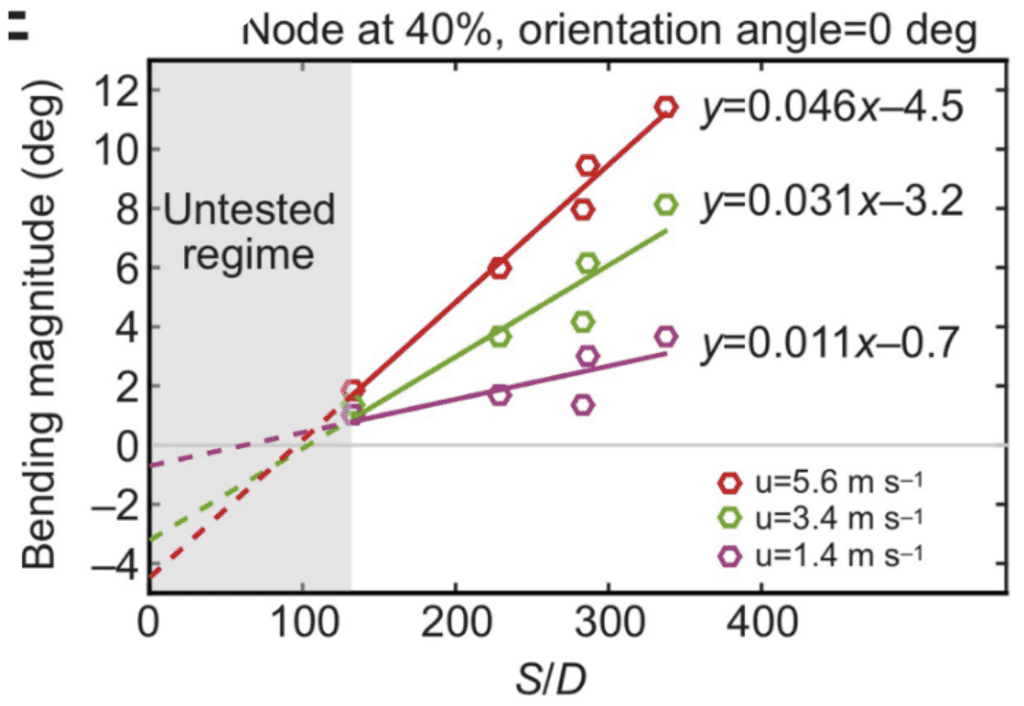
 Fig. 3 Bending magnitude increases approximately linearly with the arc length to diameter (S/D) ratio of the whisker. Results are shown for a node 40% out along each whisker and at airflow speeds (u) of 1.4, 3.4 and 5.6 ms^-1 (Yu et al., 2016).

Whisker vibration is also affected by airflow. Vibrissae typically vibrate in air at frequencies related to their resonance modes which can be described by Equation (1).

\begin{equation}
f_n=\left(\frac{\lambda_nD}{4S^2}\right)\frac{(E/\rho)^{\frac{1}{2}}}{2\pi}
\end{equation}

Equation 1 gives the theoretical frequency of different resonance modes of the rat whiskers. D represents the whisker base diameter, S the whisker arc length, λ_n the coefficient related to the mode number n, E is Young’s modulus, a value related to the whisker elasticity, and  ρ represents the density of the whisker (Yu et al., 2019).  

Once airflow hits whiskers, the vibrissae bend and oscillate close to their resonance modes around a new average position (Yu et al., 2016). The vibrational magnitude is proportional to bending magnitude as a response to airflow. Similarly to bending magnitude, the S/D ratio scales linearly with the vibration magnitude of the whisker and increases along its arc length (Yu et al., 2019).

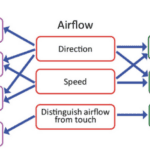
The neuronal response related to the effect of airflow on whiskers indicates the contribution of many variables in signal encoding. The neuronal firing rate increases with airflow speed or stimulus magnitude, indicating a relationship between bending magnitude, vibration magnitude, and neuronal encoding (Yu et al., 2019). Each neuron reacts to a preferred airflow speed which affects both the bending and vibration magnitude as well as the vibration direction. Changes in airflow speed alter the mechanical state of the vibrissae and affect the firing rate of each neuron, which will tend to fire at more rapid rates when a whisker is affected by its preferred airflow direction. Lastly, neurons tend to fire at rates similar to the resonance frequency of the whisker under the effect of airflow. The relationships between properties of airflow, mechanical response of vibrissae, and information encoding through neurons is summarized schematically in Figure 4 (Yu et al., 2019).

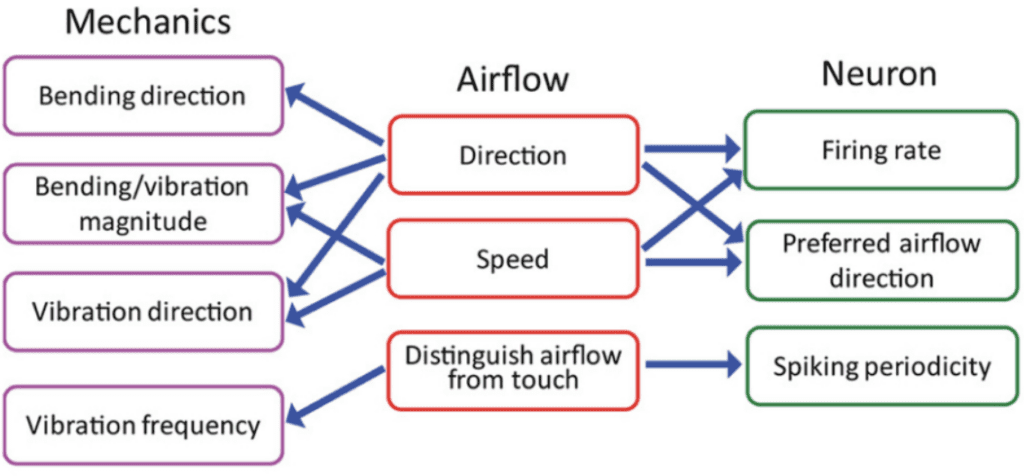
Fig. 4 Relationships between the whisker’s mechanical response, the physical parameters of airflow, and the responses of primary sensory neurons in the Vg (Yu et al., 2019).

From the current understanding of whisker information gathering, it becomes clear that the sensory information provided and encoded in airflow and physical touch are very different. During whisking on surfaces, bending direction depends on many factors, such as the object shape, texture roughness, and whisker trajectory. In contrast, vibrissae always bend in the direction of airflow when subjected to such a stimulus. When responding to airflow, all whiskers vibrate simultaneously near their respective resonance frequencies, while only whiskers which have undergone stick and slip will experience a vibration that will eventually damp out (Yu et al., 2019). These are only a few of the many differences in vibrissae behavior when gathering sensory information in air and on surfaces. 

While many hypotheses are supported by evidence, the encoding of information by whiskers and neurons has yet to be fully understood. Understanding the principles of sensory functions of rat whiskers will provide information on the sensory system of many other animals with similar anatomy.

Whiskers in Water – Harbors Seals, Masters of Stalking

Seals are pinnipeds, a group of marine mammals with front and rear flippers. Harbor seals (Phoco vitulina) have spotted furs and live on the coasts of continents in the northern hemisphere. They often hunt in dark, murky waters, meaning they cannot solely rely on their eyesight for navigation (Hanke et al., 2010). Documentation of blind, healthy seals living on Gertrude Island in Washington State shows that seals can hunt for food without sight (Zheng et al., 2021). Furthermore, an experiment by Dehnhardt et al. (2001) found that blindfolded harbor seals could track the exact path of a small sized experimental submarine with a ten-second delay and an 80% accuracy (Figure 5). Instead of eyesight, seals use their whiskers to orient themselves and hunt prey. When a seal’s whiskers intersect the vortices generated by a swimming fish—also called a wake—its whiskers will perceive the wake signal and guide the seals to follow the exact path that the fish has swum. An experiment by Renouf in 1979 showed that seals with cut-off whiskers took longer to catch trout than seals with full whiskers (Zheng et al., 2021). Moreover, when a seal’s whiskers are entirely covered by a wire mesh, the whiskers do not respond to flow stimuli (Dehnhardt et al., 1998); this also makes the seals unable to follow the trail of a small submarine in water (Dehnhardt et al., 2001). These experiments show that whiskers, which guide seals in hunting prey, are crucial to their survival. Seals can precisely track swimming fish due to the undulated and tapered shape of their whiskers; this allows them to be extremely sensitive to the wake frequencies of swimming fish while minimizing disturbances caused by their own movement through the water.

Fig. 5 Blindfolded harbor seal tracks the exact path that the submarine has taken (solid yellow line) with a 10 s delay rather than the direct path from its origin to the submarine location (dotted yellow line) (Zheng et al., 2021).

Hyper Sensitive Whiskers

Seal whiskers are sensitive to movements of less than one micrometer (Wang, 2017). They can perceive single vortex rings, benthic fish-like breathing, and flow speeds 500-2000 times lower than a seal’s swimming speed (Zheng et al., 2021). With a sensitivity range of 20 Hz to 1000 Hz and an optimal sensitivity of around 80 Hz, harbor seal whiskers can easily detect wake generated by swimming fish exceeding 100 Hz (Zheng et al., 2021). Seals can detect the size of a swimming fish, an evolutionary advantage allowing them to estimate the caloric gain of pursuing a hunt (Zheng et al., 2021). Since the trail length and vortex sizes of a wake are related to the size of a moving object in water, different frequencies and patterns detected by whisker mechanoreceptors encode information about the swimming fish’s size (Wieskotten et al. 2011). In addition, since flow vortices from fish remain detectable minutes after a fish has swum in the trail, seals can detect fish up to 180 meters away; this sensitivity range is comparable to dolphins’ echolocation (Zheng et al., 2021).

Such high sensitivity may be due to harbor seals’ highly innervated follicle-sinus complexes, which are ten times more innervated than those of land mammals (Zheng et al., 2021). The whiskers are innervated by deep vibrissal nerves at the base of their follicles, and there are an estimated 128,858  axons in the snout of a harbor seal (Jones & Marshall, 2019). Various nervous structures in the follicle-sinus complex play different roles in enhancing the sensitivity of the whisker mechanoreceptors: for instance, the largest sinus thermally protects the innervation in the lower cavernous sinus, which maintains whisker sensitivity (Jones & Marshall, 2019).

Another contributing factor to seals’ high sensitivity may be the variety of whisker sizes, which allow a broad range of frequencies to be detected. Seal whiskers can be modeled as vibrating cantilevers and their natural vibration frequencies are directly affected by geometric and material properties. The following formula is used to estimate the natural frequency of the seal whiskers:

\begin{equation}
fn=\frac{1.94t}{L^2}\sqrt{\frac{E}{\rho}}
\end{equation}

where f_n is the natural frequency of a uniform rectangular cantilever, t is the thickness, L is the length, ρ  is the density, and Young’s Modulus E is estimated to be 68 (Zheng et al., 2021). Although not entirely representative of the whisker’s true undulated and tapered structure, this modeling helps highlight the significant effect of the whisker length L in relation to a whisker’s natural frequency f_n (Zheng et al., 2021). The natural frequencies’ dependence on whisker dimensions suggests that the diverse lengths of a seal’s whiskers allow sensitivity to many different natural frequencies. In addition, the sinusoidal shape of the whiskers (Figure 6) creates less drag in the water, reducing self-induced noise and allowing greater sensitivity to other animals’ wakes.

Fig. 6 Comparison of a smooth California sea lion whisker and an undulated harbor seal whisker. Notice the undulations every 1-3 mm on the harbor seal whisker (Murphy et al., 2013).

Self-Noise Cancellation

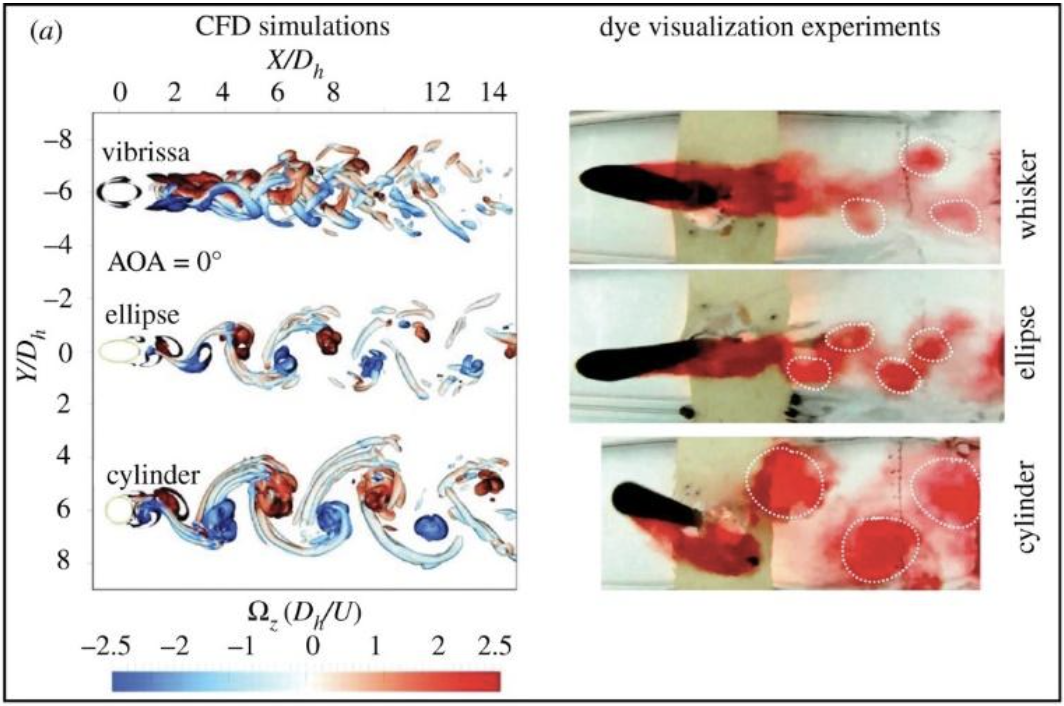
Typically, a cylinder moving through water would generate Karman vortices (see glossary) behind itself, causing self-induced disturbances (Figure 7). These alternating swirling vortexes would hit a cylindrical whisker from downstream, causing it to vibrate. However, seal whiskers are undulated with a peak every 1-3 mm and have elliptical cross sections (Wang, 2017). This shape reduces noise from self-induced vortices, as whiskers with elliptical cross sections generate Karman vortices that are more downstream than those generated by cylindrical cross sections (Figure 8) (Hanke et al., 2010). In addition, the undulated shape disrupts the coherence of the shedded Karman vortices (Zheng et al., 2021). Therefore, the disturbances caused by self-induced vortices will be suppressed, allowing the whiskers to traverse the water without significant vibration due to their own movement. The importance of noise suppression can be demonstrated by calculating the vortex shedding frequencies assuming the whiskers were not undulated.  The formula for the frequency of vortex-induced vibrations (VIVs) is

\begin{equation}
f_{VIV}=(St\times U_{\infty})/D
\end{equation}

Using an average whisker diameter of D = 1 mm, a seal’s typical swimming velocity of U_∞ = 0.5 m s⁻¹, and a Strouhal number of St = 0.21, the vortex vibrations were estimated to be around 100 Hz (Zheng et al., 2021). This f_VIV ∼ 100 Hz corresponds to the typical wake frequency of swimming fish. If the whiskers were not undulated and thus capable of suppressing self-induced noise, differentiation of self-induced wakes and wakes generated by other species would be extremely difficult.

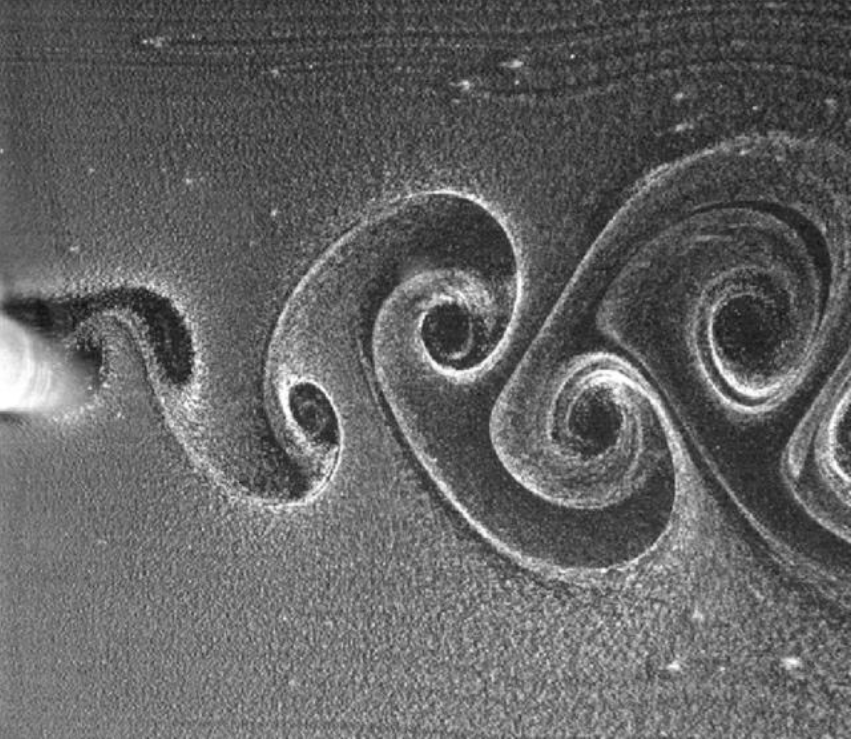
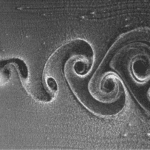
Fig. 7 Visualization of a Karman Vortex generated by an object moving in water (Huang et al., 2019).

Fig. 8 Effect of undulations on vortex-induced vibrations. With an undulated whisker, Karman vortices are incoherent, whereas a cylinder creates visible Karman wakes (Zheng et al., 2021).

Mechanisms of interaction:

During wake detection, harbor seal whiskers are held erect, with the length of the whisker oriented perpendicular to the direction of the water flow (Zheng et al., 2022). The whiskers vibrate at the same frequency as the vibrations generated by the swimming prey. These vibrations encode information about the fish’s size and shape, as well as the speed and direction of swimming (Zheng et al., 2022). The relationship between whiskers’ orientation in water flow and the intensity of vortices induced was discovered by Murphy et al.’s experiments (Zheng et al., 2021). These experiments showed that the attack angle that generates the least self-disturbances is 0 degrees between the major axis and the flow direction, i.e., when the longer diameter of the elliptical cross-section is parallel to the water flow (Zheng et al., 2021). Furthermore, experimental findings by Wang & Liu showed that at an angle of attack of 30 degrees, the effectiveness of vortex-induced vibration suppression diminishes (Zheng et al., 2021). However, the actual angles at which seal whiskers are oriented are unknown; there is likely no fixed orientation due to the movement of a seal head during swimming. The exact mechanism of interaction between the whiskers and the wake is yet to be discovered, but two current hypotheses are stick-and-slip and slaloming.

Stick and slip

Similar to the stick-and-slip mechanism of rat whiskers, this mechanism puts for a two-part movement by the whisker. During the stick movement, which occurs in a steady flow, the whisker bends steadily in the direction of the flow and vibrates at a natural frequency (Muthuramalingam & Bruecker, 2019). When a disturbance from a fish’s wake is intercepted, the whisker will slip: it momentarily stops bending in the flow direction, instead tilting against the current and ultimately returning to its initial position, vibration with the same frequency as the wake vortices (Muthuramalingam & Bruecker, 2019).

Slaloming

Swimming fish generate a series of Karman vortices called a Karman street. The slaloming model proposes that the whiskers slalom—move in an “S” fashion—around the wake vortices (Seal-whisker-inspired Sensing), thus vibrating at the same frequency as the wake-induced vortices (Beem & Triantafyllou,  2015). This can be interpreted as a capture of vibrational energy from the wake by the whiskers. This frequency locking has been found to occur even at large distances away from the wake source, and this slaloming motion has been observed in the behavior of fish swimming behind other fish’s trails (Zheng et al., 2021).

Antenna on Land – Insect Antennae Deformation Driven by Blood-Pressure Alternation

What are Insect Antennae?

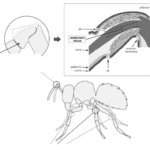
Insects have segmented bodies supported by exoskeletons, which have evolved into three distinctive but interconnected units: head, thorax, and abdomen. The head supports a pair of antennae, which are well-evolved appendages with various forms of complex sensory organs (Chapman et al., 2013) (Figure 9). The primary function of the antenna is to assess the chemical and physical properties of the environment, for example, to locate mates and engage in combat (Hanks et al., 1996). Detection is performed using innervated chemosensory and mechanosensory organs arranged on the antennae. A single antenna typically has multiple sensory organs with different properties. Applications to this pair of appendages include but are not limited to feeling an object’s surface, sensing surrounding temperature, and detecting sounds and movement of minuscule particles in the air. (Loudon, 2009).

Fig. 9 A bee (Bombus perplexus) with pollen on its head sitting on a petal. Notice the pair of antennae on its head (Types of Insect Antennae, 2019).

How do insects control the movement of their antennae?

Insect antennae have three basic segments: the scape, the pedicel, and the flagellum, also known as the flagellomeres. The pedicel is further divided into two basal segments that utilize muscles to control antennal movement in almost any direction (Loudon, 2009). At the same time, the other parts of the antennae can bend and twist controllably without aiding muscles. It is proposed that the deformation of insect antennae significantly depends on the structure of the antennae and blood supply (Donley et al., 2022). The hypothesis is that antennal deformation results from hemolymph alternation, where the structural and tensile properties of the antennae of Periplaneta americana (American cockroach), Manduca sexta (Carolina hawkmoth), and Vanessa cardui (painted lady butterfly) are studied (Donley et al., 2022).

The features of blood-filled flagellomeres deformation:

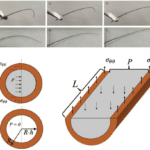
Insect antennae can be conceptualized as blood-filled hollow fibers. The role of blood is to distribute the applied load on the antennal cuticular shell. It is examined by solid mechanics and models, considering individual flagellum as a circular tube filled with an incompressible fluid. The interaction of the blood with the cuticular wall is regarded through the generation of its pressure (Donley et al., 2022).

To evaluate the stresses in the modeled tube filled with liquid, G. Donley applied Hooke’s law for the tube’s material, relating the compression modulus and shear modulus to Young’s modulus and Poisson’s ratio to formulated equations representing the stress balance in the radial direction for the tube wall (Donley et al., 2022):

\begin{equation}
\frac{d\sigma_{rr}}{dr}+\frac{1}{r}(\sigma_{rr}-\sigma_{\theta\theta})=0
\end{equation}

In this equation, σ_zz, σ_rr, and σ_θθ are derived from Hooke’s law for stress and strain related to the tube’s material in the cylindrical coordinate system (z, r, θ).

\sigma=E\epsilon\; \textrm{and}\;E=2G(1+v)

\sigma_{rr}=(\lambda+2G)\epsilon_{rr}+\lambda(\epsilon_{\theta\theta}+\epsilon_{zz})

\sigma_{\theta\theta}=(\lambda+2G)\epsilon_{\theta\theta}+\lambda(\epsilon_{rr}+e_{zz})

\sigma_{zz}=(\lambda+2G)\epsilon_{zz}+\lambda(\epsilon_{\theta\theta}+e_{rr})

Where

• σ is the stress [Pa];
• is the strain (ΔL/L);
• E is Young’s modulus of elasticity in tension or compression [Pa];
• v is the Poisson’s ratio;
• G is the shear modulus [Pa].

Equation (4) follows two boundary conditions with R₁ representing the inner radius and R₂ representing the outer radius of the modeled circular tube (Donley et al., 2022):

\begin{equation}
\sigma_{rr}(R_1)=-P\; \textrm{at}\; r=R_1
\end{equation}

\begin{equation}
\sigma_{rr}(R_2)=0\; \textrm{at}\; r=R_1
\end{equation}

Positive pressure indicates fluid compression and negative pressure indicates stretching. Therefore, Equation (5) has a negative sign in front of pressure P. In solid mechanics, positive stress signifies tension and negative compression (Donley et al., 2022). Therefore, when pressure P < 0, the right-hand side of Equation (5) gives a positive radial stress output, resulting in tension on the tube wall. And vice versa, when pressure P > 0, the right-hand side of Equation (5) gives a negative radial stress output, leading to compression of the tube wall.

To obtain the stresses and strains in the antenna analytically, the antennal inflation/contraction is analyzed in two scenarios: antennal deformation by applying non-zero-external-force (NZF) and antennal deformation under zero-external-force (ZF) (Donley et al., 2022).

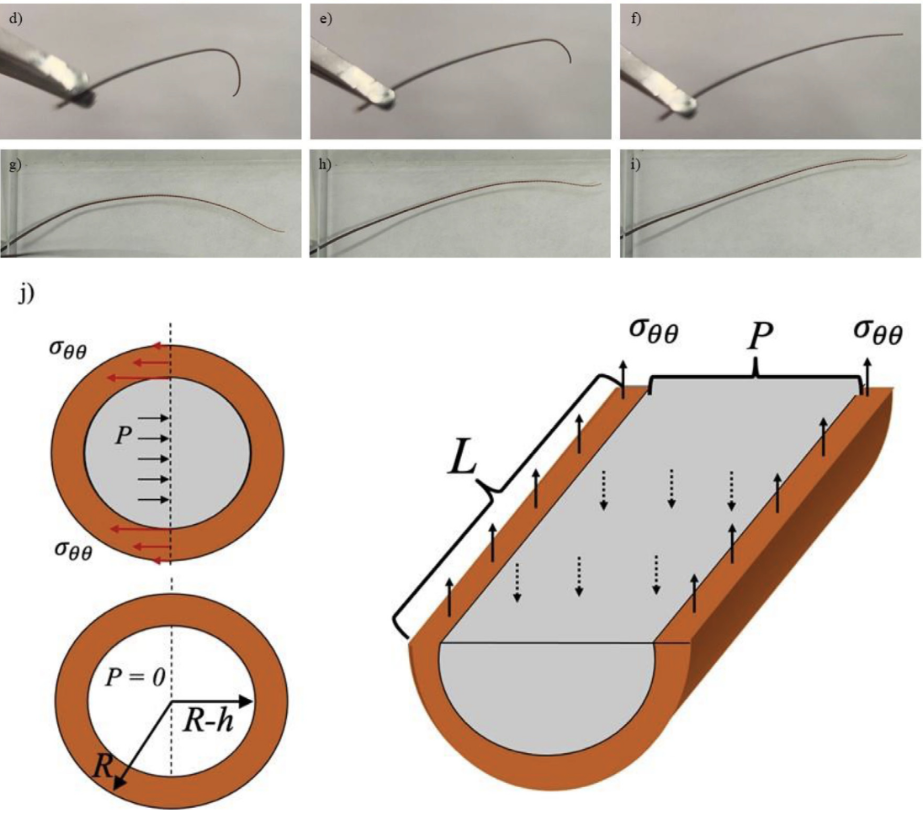
Fig. 10 (d-f) Squeezing the base of the antenna removed from Periplaneta americana (American cockroach), the curved antenna tip can be straightened. (g-i) Restrained cockroaches in a paper envelope could move the antenna freely between the two glass slides with an air gap between them. (j) The flagellomere is modeled as a circular tube with outer radius R₂ and inner radius R₁, and length L is filled with an incompressible liquid, shown in gray. Flagellomere diagonal and longitudinal sections illustrate free body diagrams for the zero-external-force scenario when the hoop stress counteracts the internal pressure P in the cuticle (Donley et al., 2022).

Antennal deformation by applying non-zero-external-force (NZF)

In this case, each flagellomere experiences the same external force F to the ends of the antenna. The liquid is considered incompressible; the liquid column length L is stretched to L + ΔL and its radius changes from R₁ to R₁ + ΔR₁. The volume of liquids inside the tube is conserved as the tube ends are sealed. Assuming the tube deformation are small, where ΔL << L, and ΔR₁ << R₁, the condition of the volume conservation can be written in terms of displacement ΔR₁ of the internal wall of the tube as (Donley et al., 2022):

2\pi R_1\Delta R_1L+\pi R_1^2\Delta L=0

\begin{equation}
\frac{2\Delta R_1}{R_1}+\frac{\Delta L}{L}=0
\end{equation}

The equation can be further developed with the strains ε_zz=ΔL/L,rr=dudr, ε_θθ=du/dr, where u represents the radical displacement of the material particles, and r represents the radial coordinate in the tube wall (Donley et al., 2022),

\begin{equation}
\epsilon_{zz}=-2\epsilon_{\theta\theta}=-\frac{2\Delta R_1}{R_1}
\end{equation}

This equation implies that each radial cross-section of the tube is stretched evenly. When ΔR₁ > 0, the tube expansion results in ε_zz < 0, which is the contraction of tube length. Vice versa, when ΔR₁ < 0, the tube expansion results in ε_zz > 0, which is the extension of tube length.

Use the balanced force equation and relate the pressure P with the applied force F (Donley et al., 2022):

\begin{equation}
F=-\pi R_1^2P+(\pi R_2^2-\pi R_1^2)\sigma_{zz}
\end{equation}

Thus, Equation (9) defines the generated pressure, which describes the tensile experiments under the assumption that the insect antennae are sealed tubes.

Antennal deformation by zero-external-force (ZF)

In this case, the deformation of the antennae is driven by the increase or decrease of blood pressure using an insect pulsatile organ (Figure 10). Thus, the blood volume inside the tube is not conserved in this scenario. The pressure generated by the pulsatile organ is considered the driving parameter. Since the total force acting on the object is zero, Equation (9) can be reorganized to (Donley et al., 2022):

\begin{equation}
0=-\pi R^2_1P+(\pi R_2^2-\pi R_1^2)\sigma_{zz}
\end{equation}

Where Equation (10) can be rearranged to obtain the axial stress σ_zz:

\begin{equation}
\sigma_{zz}=\frac{\pi R^2_1P}{(\pi R_2^2-\pi R_1^2)}
\end{equation}

Axial stress zz in Equation (11) can be replaced by Hooke’s law of: σ_zz = (λ+2G)ε_zz + λ(ε_θθ+ε_rr). Thus, the resulting equation is (Donley et al., 2022):

\begin{equation}
\epsilon_{zz}=\frac{\pi R_1^2P}{(\pi R_2^2-\pi R_1^2)(\lambda +2G)}-\frac{\lambda}{(\lambda+2G)}(\epsilon_{\theta\theta}+\epsilon_{rr})
\end{equation}

Finally, using Equations (7)-(9) and (11)-(12), the stress and strains in the antenna can be solved analytically.

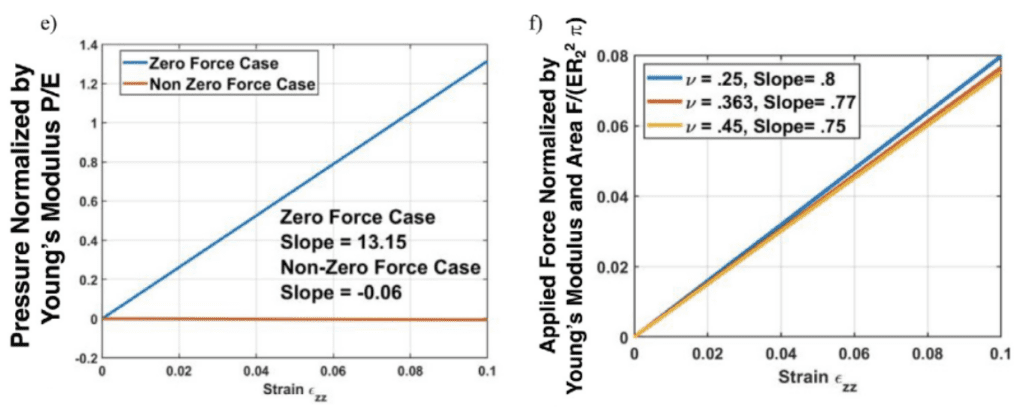
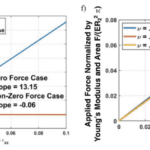
Fig. 11 (e-f) The dependence of dimensionless pressure on the axial strain zz for two distinct scenarios (Donley et al., 2022).

The looping or bending of insect antennal flagellum can be controlled by blood pressure depending on the antennal pulsatile organs and stress conditions (Donley et al., 2022). In addition, there is linear dependency in both scenarios shown in Figure 11, revealing that blood is associated with the cuticle to distribute the applied load. The blood pressure within an insect antenna increases or decreases with respect to the blood pumping of antennae inflation/contraction. With more knowledge of mechanical properties of insects discovered, there will be a variety of further developments in insect biology and engineering applications.

Antenna in air – Insect hearing

Insect Hearing

Not only can insect antennae serve tactile (Dirks & Dürr, 2011) and olfactory functions (Hansson & Stensmyr, 2011), but they can also help insects hear. 

Hearing is vital for insects because it is used for intraspecies communication and predator avoidance. Intraspecies communication can include sexual communication to find a partner (Holderied & Neil, 2021) and social communication to recruit foragers, as in the case of bees’ waggle dance (Hunt & Richard, 2013). Somes species, like the Lepidoptera, can sense specific frequencies, like the ultrasound of the bat, and avoid them (Holderied & Neil, 2021). There are two main ways by which insects can detect sounds: pressure changes and particle oscillations. Some insects have the organ tympanum, which gives them long-range hearing abilities by allowing them to sense and convert pressure oscillations to neuronal signals (Holderied & Neil, 2021). However, this essay will focus on insects—mosquitoes and flies, both of which use hearing for mating purposes—that use antennae to detect and process near-field oscillations and “hear.”

Antennal Hearing 

Unlike tympanal ears that detect scalar quantities, antennal ears detect vector quantities (Römer, 2020). They hear using Johnston’s organs, the second segment of the antennae Figure 12. Many insects can “hear” because antennae are light enough to obtain information about sound from the changes in media particle velocity. The detection of particle velocity is calculated by detecting drag on the antenna, as shown in Equation (13)

\begin{equation}
F+b_vP
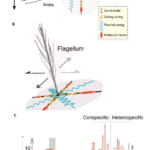
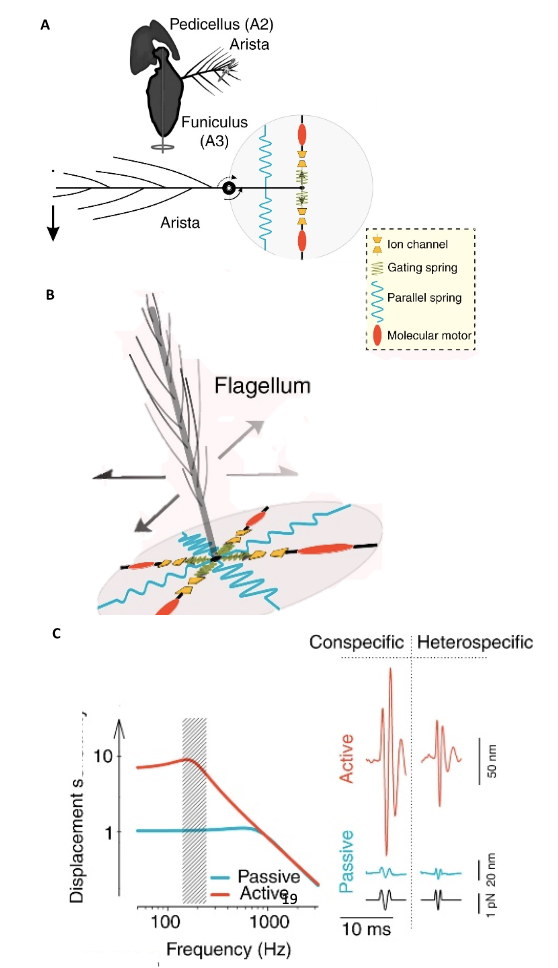
\end{equation}

in which b is the viscous drag of the antenna and v_p is the particle velocity (Jackson & Windmill, 2016). The Johnston’s organs on the antennae can sense touch, gravity, wind, and sound by “monitoring stimulus-induced movements of the antenna’s muscle-free distal part” (Effertz et al., 2010). There is no tuning involved, though the antennal movements will certainly cause changes in tension and compression. Simply put, when subject to external forces, like the vibrations from sound, distal parts of the antenna move, the Johnston’s organ senses the movements, translating them into nerve impulses (Hunt & Richard, 2013). The sound signals are transduced by mechanosensory neurons and amplified through interaction between directly gated mechanotransducer channels in the neurons, and molecular motors (Figure 13 (A) (B)) (Albert & Kozlov, 2016).

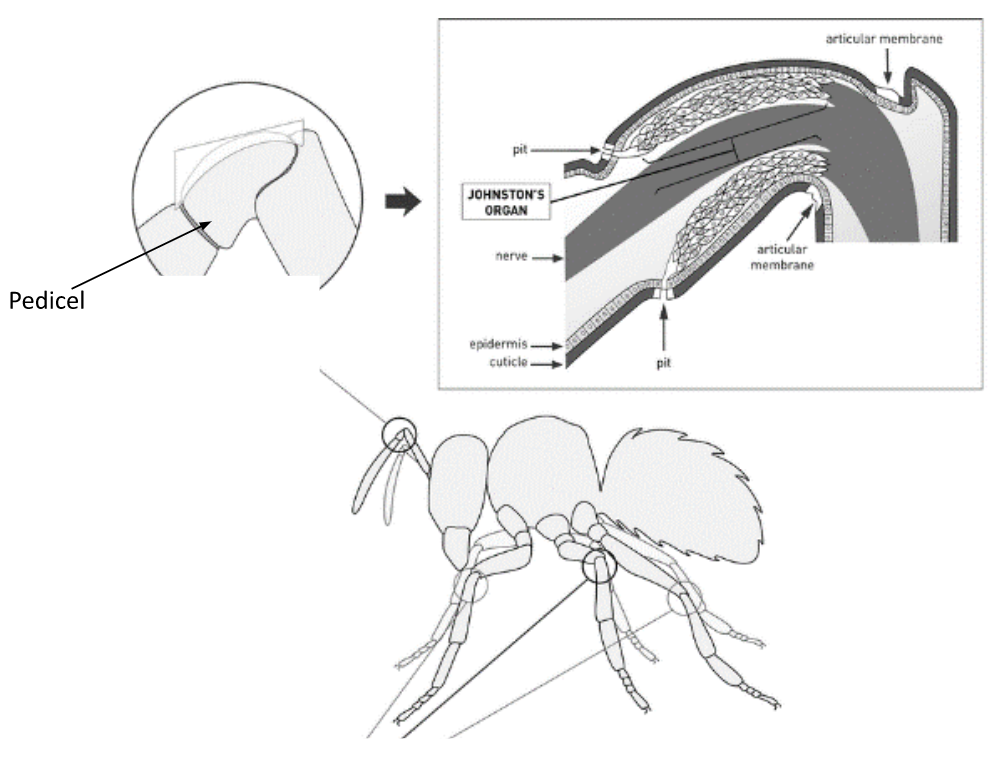
Fig. 12 The Johnston’s organ is located in the pedicel, and it is the second segment of the antenna (Adapted from Hunt & Richard, 2013).

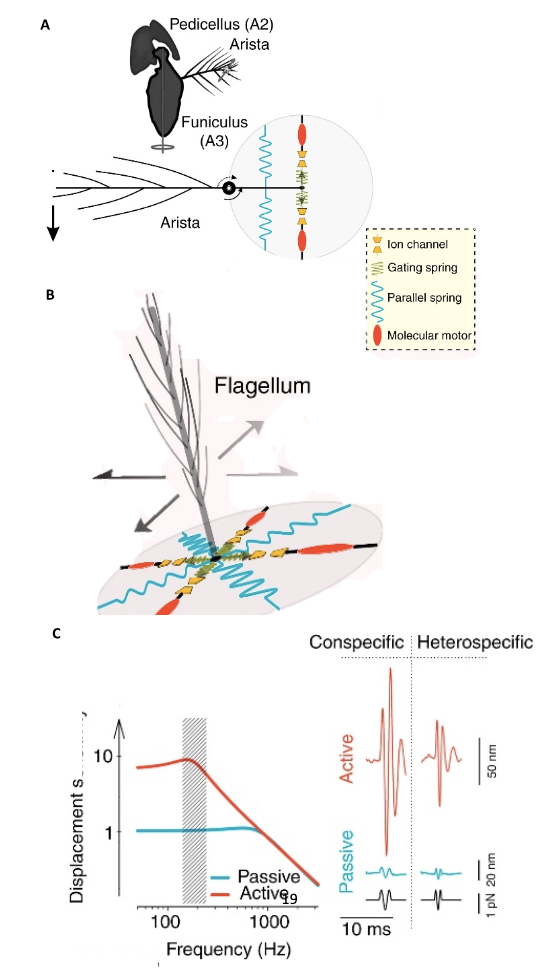
Fig. 13 “Sound system” of Drosophila and mosquitoes (A) Sound receivers (arista) of Drosophila are linked to mechanosensory neurons of Johnston’s organs that have gated mechanotransducer channels that help with amplification. (B) Sound receivers (flagella) of mosquitoes are linked to mechanosensory neurons of Johnston’s organs, with gated mechanotransducer channels that help with signal, or sound, amplification. (C) The displacement sensitivity of Drosophila antennae is greater for active amplification systems, particularly at the range of mating songs (Adapted from Albert & Kozlov, 2016).

Modeling

Without considering the aforementioned blood-pressure-induced antennal displacements, the movement of the antennae can often be modeled as a moderately damped harmonic oscillator, shown in Equation (14), and (15). An antenna can be a reverse rotating pendulum, or a beam supported by a spring. In both the insects, flies and mosquitos, these antennae have non-linear behavior.

\begin{equation}
\left[\frac{d^2}{dt^2}+2\gamma\frac{d}{dt}+\omega_0^2\right]x(t)=0
\end{equation}

\begin{equation}
x(t)=A\cos\cos(\omega_0t+\phi)
\end{equation}

The damped harmonic oscillator equation is a second order linear differential equation. The second derivative is the acceleration, the first derivative is velocity, with the γ acting as the damping factor, and ω₀² is the oscillation from the spring force. The solution to this equation is a sinusoid, with constant amplitude A, phase ϕ, and frequency ω₀ (Chong, 2021).

Modeling for Drosophila

At first glance, it seems that Drosophila is modeled by a moderately damped harmonic oscillator; the antennae are a rotating pendulum, with one degree of freedom (Holderied & Neil, 2021). However, experimentally, these antennae have non-linear mechanics (Figure 14) (Holderied & Neil, 2021). When stimulated by sound, the effective stiffness—the stiffness between the Johnston’s organ and the distal part of the antenna—changes, which alters the resonant frequency (Jackson & Windmill, 2016). This is likely caused by neurons contributing energy to the oscillation. The energy from neurons counteracts the friction and decreases the damping, allowing for sharper tuning (Avitabile et al., 2009). In addition to being able to add energy, the neurons in the Johnston’s organ amplify the sensitivity of the antenna to sound by producing non-linear compression, frequency-specific amplification, self-sustained oscillations, and power gain (Effertz et al., 2010). It is important to note that power gain in fruit flies necessarily violates principles in thermodynamics like equipartition, in Equation (16), which states that each degree of freedom is

\begin{equation}
1/2K_bT
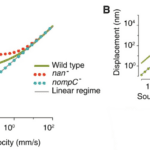
\end{equation}

in which K_B is the Boltzmann’s Constant, and T is the temperature, in Kelvin (LibreTexts, 2022), and the fluctuation-dissipation theorem (Effertz et al., 2010), which essentially says that there is a relationship between random forces by thermal energy and external disturbances, like kinetic energy, turning into thermal energy, affecting the equilibrium (Kubo, 1966). In the case of the flies, the kinetic energy of the antennae seems to be able to increase out of nowhere; therefore, this violates equipartition and the fluctuation-dissipation theorem. It is also interesting to note that the self-oscillation of a Drosophila antenna is non-sinusoidal. According to Jackson and Windmill (2016), it “vibrates as if it were switching between two extreme displacements,” but it obeys the principle of equipartition (Römer, 2020). Compared to the self-oscillations, “active listening” with amplification from transducers has a much greater antennal displacement sensitivity in the frequency range of the mating song than the “song” created by wingbeat (Figure 13 (C)) (Albert & Kozlov, 2016).  This amplification produces compressive non-linear behavior in the antennal receiver, causing big displacements for smaller stimuli in that frequency range (Figure 15).

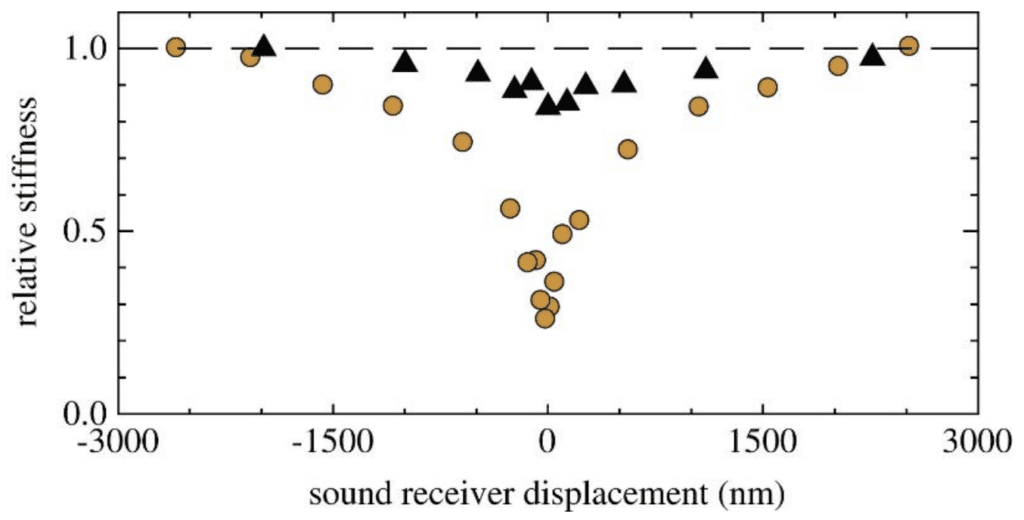
Fig. 14 A plot demonstrating the non-linear antennal behavior of Drosophila (yellow) and mosquitoes (black). The hatched line is linear. Drosophila antennal behavior is apparently more non-linear than mosquito antennal behavior (Adapted from Effertz et al., 2010).

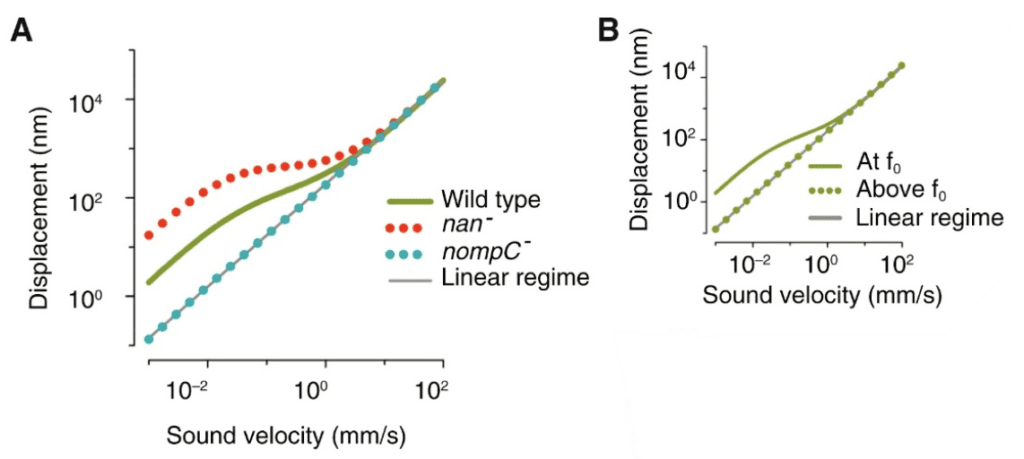
Fig. 15 Plots showing Drosophila compressive non-linearity in amplification. (A) The effect of mechanotransduction channels on compressive non-linearity is demonstrated. The wild type has relatively large displacements for small stimuli. The nan- is removing the Nanchung channel, which enhances the non-linearity. The nompC- is removing the NompC channel, which results in linearity. (B) Plot that shows frequency-dependence of non-linear amplification. f₀ is the receiver’s best frequency. When the frequency is too high, the displacement returns to linear behavior (Adapted from Albert & Kozlov, 2016).

Modeling for Mosquitos

Like Drosophila, mosquitoes have mating songs and antennae that are non-linear oscillators, caused also by neurons in transducer modules (Albert & Kozlov, 2016). Although, like Drosophila, male mosquitoes have antennae that do not bend, these antennae have 2 degrees of freedom (Albert & Kozlov, 2016)—rotational and translational—so they can be modeled like a beam supported by a spring, a harmonic oscillator (Jackson & Windmill, 2016). Also similar to Drosophila, mosquitos’ harmonic oscillator is damped: caused by the stiffness between the Johnston’s organ and the flagellum and the feathery antennae moving through the air (Jackson & Windmill, 2016). The oscillation is sinusoidal and has a primary resonance approximately equal to the frequency of a female mosquito’s flight tone (Jackson & Windmill, 2016). Again, mosquito antennal motion is non-linear, but unlike in the case of fruit flies, there is only a small change in the effective stiffness of the antenna (Jackson & Windmill, 2016). Additionally, mosquitos’ antennae also self-oscillate.  Aside from the relatively simpler damped oscillator model, a more comprehensive model has been created for mosquitoes: the continuum model stemming from the integrate-and-twitch model (Avitabile et al., 2009). In the integrate-and-twitch model, the antenna is a damped oscillator coupled to threads of scolopidia that twitch and cause an impulsive force. The twitching is caused by ion channels that open and close based on the amplitudes of the antenna. This model is mainly described by Equations (17) and (20). The first equation describes the antennal motion, by angular displacement, as an oscillator, subject to the sound field, M_s(t), and the mechanical action of threads, M_t(n), in which n collects the thread potentials. Equation (18) is the sound field equation.  The sound field is modeled as a single harmonic, with X_s as the amplitude. Equation (19) describes the mechanical action of threads, modeled by a series of impulsive torques. The second equation, (20), describes the change in thread potential, with l₁ as discharge rate, and l₂ as charge rate, subject to the antennal displacements, threat potential, and time, due to the Heaviside function G, that is Equation (21).

\begin{equation}
\ddot{\theta}+c\dot{\theta}+k\theta=\frac{1}{J}(M_s(t)+M_t(n))
\end{equation}

\begin{equation}
M_s(t)(\omega_st)
\end{equation}

\begin{equation}
M_t(n)=\sum_{j=-N}^Nm_j(n_j)=\sum_{j=-N}^N\sum_{k=1}^\infty fk\Delta a\delta(t-t_{jk}(n_j))
\end{equation}

\begin{equation}
\dot{n}=-l_1n+l_2G(\theta,n,t)
\end{equation}

\begin{equation}
G_j(\theta,n_j,t)=H(\theta j\Delta a-s)\left[1-\sum_{k=1}^\infty H(t-t_{jk}(n_j)-H(t-t_{jk}(n_j)-d))\right]
\end{equation}

The Heaviside function that couples the threads to the antenna. Simply, it says the j^th thread can only charge if there is a compression θ jΔa greater than s, some threshold value, and the refractory period d must have passed since the previous twitch. In layman’s terms, the function G allows charging only if there is a big enough antennal displacement and enough time has passed before the previous charge. The continuum model is the same thing, except the nonlinearity is expressed in the nonlinear function f_ho, shown in (21). This function is too complicated for the scope of this essay, so no further explanation will be offered apart from its existence in Equation (21). The continuum model equation, Equation (22), is derived from the integrate-and-twitch model. Since the mechanical action of threads is correlated with antennal displacement, it can be taken into account by a non-linear function f_ho, which depends on the antennal displacement and velocity.

\begin{equation}
\ddot{\theta}+c\dot{\theta}+k\theta+f_{ho}\left(\theta,\dot{\theta}\right)=\frac{1}{J}\left(M_s(t)\right)
\end{equation}

The mosquitoes’ method of listening for mates seems to be more complicated than that of the Drosophila. Wingbeat-matching in mosquitoes produces higher harmonics than the fundamental frequency, and this higher harmonic is not within the range of mosquito hearing. However, distortion products—additional tones generated from “two tones interacting in a nonlinear system”—are created from this frequency-matching, which allows the male and female mosquitoes to hear each other again (Gibson et al., 2009). Specifically, the cubic distortion product, 2f1-f2, in which f1 and f2 are frequencies of the male and female, respectively, transposes the too high frequency down (Albert & Kozlov, 2016).

Biomimetic applications of physical properties of Whiskers and Antennae

Minimally invasive biomimetic whisker-like sensors are of great interest in designing marine sensors due to the limitations of other sensors. Vision-based sensors have a limited range in dark and muddy waters, while acoustic sensors are harmful to marine animals as they may disturb their natural echolocation patterns. 

An example of seal whisker-inspired biomimicry is the development of an artificial whisker neural model using deep machine learning to find the position in two dimensions of the source of vibrations (Elshalakani et al., 2020). The predictions of the vibration source according to the wakes perceived were accurate, with errors of 1 cm in the x-direction and 3 cm in the y-direction (Elshalakani et al., 2020). Further refinement of these technologies could improve their accuracy and allow extension to the three-dimensional space. These biomimetic sensors could then be used as oil spill trackers, submarine navigation sensors, marine species monitoring, and dangerous flow warning (Lippsett, 2020).

Similarly, biomimetic applications of insect antennae include the detection of electromagnetic wave frequencies. For instance, Nader Behdad’s prototypical designs apply the principles of insects’ hearing of vector quantities to make antennae with the ability to perceive signals from various directions (Knisely, 2011). These biomimetic antennae could serve the same functions as typical satellite antennae used in electronic devices, but at a much smaller scale. The smaller size of the antennae may increase the efficiency and speed of signal processing, resulting in enhanced wireless electronic applications (Knisely, 2011).

Conclusion

Although it is well known that whiskers and antennae serve sensory functions, the purpose and method by which they enhance senses are not necessarily the same throughout all species. We sought to investigate and compare the causes and effects of whisker and antennal functions in various species. 

Many animals live in environments that are not conducive to the effective use of certain sensory functions, such as sight, so they compensate by enhancing other senses through structures like whiskers. For example, rats, which often live in darkness, perceive the world around them with their whiskers by whisking and detecting airflow. Whisking involves short sweeps of the whiskers with frequencies between 5 and 15 Hz and arcs of 25 to 75 degrees. During this process, the whiskers undergo stick-slip events, in which whiskers “stick” to a surface and “slip” following a continually applied force that overcomes friction. The current hypothesis—the temporal hypothesis—indicates a correlation between the kinetic effects of stick-slip and texture recognition; different surfaces cause different neuron firing rates. Whiskers detect airflow by bending proportionally to the airflow velocity, providing rats with sensory information.  

Similar to the rats, seals living in murky waters cannot rely on their eyesight, so they use their whiskers for navigation and hunting. The whiskers are extremely sensitive—having a frequency range of 20 Hz to 1000 Hz—able to track wake signals up to 180 m away, follow the object, as well as figure out its size. This high sensitivity could be due to their highly innervated follicle sinus complex and the different lengths of whiskers that allow the detection of different natural frequencies. The sinusoidal shape of the whiskers causes less drag and reduces the noise created by the whisker itself. The current hypotheses for interaction between whiskers and wakes are stick-slip—the whiskers “stick” to intercepted fish wake—and slaloming—whiskers move in an S-shape around the wake vortices, vibrating at the same frequencies as these vortices.  

Other animals have sensory functions that stem directly from their physiology. For example, blood pressure changes the stiffness of antennae, and insects’ flight naturally creates a frequency that can be perceived by the antennae of insects of the same species. The antenna contains the flagellum, which, based on the current hypothesis, uses blood pressure fluctuation to cause antennal movement instead of muscles. These flagella can be modeled as circular tubes with an incompressible fluid. The interactions between the blood and the tube wall can be quantified by pressure: positive pressure is the compression of the tube wall, while negative pressure is the stretching of the tube wall. Looping and bending of the flagellum can thus be controlled by blood pressure, and the blood helps distribute the applied load.

On the other hand, insect hearing from antennae allows inter and intraspecies communication. For Drosophila and mosquitoes, the antennal hearing is mostly for mating purposes and can generally be modeled as a non-linear damped harmonic oscillator, with primary resonance corresponding to the opposite sex’s flight tone. The sound signals are received and amplified by transducers in Johnston’s organs for greater sensitivity.  

Despite many physical models of whisker and antenna function, much is still to be learned about how whiskers and antennae enhance organisms’ senses, and more precise models need to be developed. Further experiments and observation are needed to determine how these enhancers and their specific mechanisms arise to obtain a complete understanding of sensing in the natural world. Such discoveries could be applied to imitate these structures and their sensing capabilities in an industrial setting. 

References

Albert, J. T., & Kozlov, A. S. (2016). Comparative Aspects of Hearing in Vertebrates and Insects with Antennal Ears. Current Biology, 26 (20), R1050-R1061. https://doi.org/10.1016/j.cub.2016.09.017

Avitabile, D., & Homer, M., & Jackson, J., & Robert, D., & Champneys, A. (2009). Modelling the Active Hearing Process in Mosquitoes. AIP Conference Proceedings, 1403(1). https://doi.org/10.1063/1.3658129

Benthic fish and animals. Polarpedia. https://polarpedia.eu/en/benthic-fish-and-animals/#:~:text=Benthic%20fish%20(also%20known%20as,extremely%20diverse%20looks%20and%20behaviour. [Retrieved Sept. 26 2022]

Chapman, R. F., Simpson, S. J., & Douglas, A. E. (2013). The insects: structure and function. Cambridge University Press. https://doi.org/10.1017/cbo9780511818202

Chong, Y. D. (2021, April 30). 5.1: The Damped Harmonic Oscillator. LibreTexts Physics. https://phys.libretexts.org/Bookshelves/Mathematical_Physics_and_Pedagogy/Complex_Methods_for_the_Sciences_(Chong)/05%3A_Complex_Oscillations/5.01%3A_The_Damped_Harmonic_Oscillator#:~:text=Dividing%20by%20the%20common%20factor,the%20damped%20harmonic%20oscillator%20equation.&text=Sometimes%2C%20we%20write%20the%20damped,x(t)%3D0

Dehnhardt, G., Mauck, B., Hanke, W., Bleckmann, H. (2001) Hydrodynamic trail-following in harbor seals (Phoca vitulina). Science 293, 102–104. doi:10.1126/science.1060514

Dehnhardt, G., Mauck, B., Bleckmann, H. (1998) Seal whiskers detect water movements. Nature 394, 235–236. doi:10.1038/28303

Diamond, M. E. (2010). Texture sensation through fingertips and the whiskers. Current opinion in neurobiology, 20 (3), 319-327. https://doi.org/10.1016/j.conb.2010.03.004

Dirks, J. H., & Dürr, V. (2011). Biomechanics of the stick insect antenna: Damping properties and structural correlates of the cuticle. Journal of the Mechanical Behavior of Biomedical Materials, 4(8), 2031-2042. https://doi.org/10.1016/j.jmbbm.2011.07.002

Donley, G., Sun, Y., Pass, G., Adler, P. H., Beard, C. E., Owens, J., & Kornev, K. G. (2022). Insect antennae: Coupling blood pressure with cuticle deformation to control movement. Acta Biomaterialia, 147, 102–119. https://doi.org/10.1016/j.actbio.2022.05.044

Effertz, T., & Göpfert, M. C., & Nadrowski, B., & Senthilan, P. R. (2010). Antennal hearing in insects – New findings, new questions. Hearing Research, 273(1-2), 7-13. https://doi.org/10.1016/j.heares.2010.03.092

Elshalakani, M., Muthuramalingam, M., Bruecker, C. (2020) A Deep-Learning Model for Underwater Position Sensing of a Wake’s Source Using Artificial Seal Whiskers. Sensors 20 (12):3522. https://doi.org/10.3390/s20123522

Gibson, G., & Russell, I. J., & Warren, B., (2009). Sex Recognition through Midflight Mating Duets in Culex Mosquitoes Is Mediated by Acoustic Distortion. Current Biology, 19(6), 485-491. https://doi.org/10.1016/j.cub.2009.01.059

Hansson, B. S., & Stensmyr, M. C. (2011). Evolution of Insect Olfaction. Neuron, 72(5), 698-711. https://doi.org/10.1016/j.neuron.2011.11.003

Hanks, L. M., Millar, J. G., & Paine, T. D. (1996). Mating behavior of the eucalyptus longhorned borer (Coleoptera: Cerambycidae) and the adaptive significance of long “horns.” Journal of Insect Behavior, 9(3), 383–393. https://doi.org/10.1007/bf02214017

Hanke, W., Witte, M., Miersch, L, Brede, M., Oeffner, J., Michael, M., Hanke, F., Leder, A., Dehnhardt, D. (2010) Harbor seal vibrissa morphology suppresses vortex-induced vibrations. Journal of Experimental Biology 213 (15): 2665–2672. https://doi.org/10.1242/jeb.043216

Holderied, M. W., & Neil, T. R. (2021). Chapter Two – Sound production and hearing in insects. In R. Jurenka (Eds.), Sound Communication in Insects (pp. 101-139). Elsevier Science. https://doi.org/10.1016/bs.aiip.2021.10.001

Hooker S. K., Andrews R. D., Arnould J. P. Y., Bester M. N., Davis R. W., Insley S. J., Gales N. J., Goldsworthy S. D., McKnight J. C. (2021) Fur seals do, but sea lions don’t — cross taxa insights into exhalation during ascent from dives. Philosophical Transactions of the Royal Society B. 3762020021920200219. http://doi.org/10.1098/rstb.2020.0219

Hunt, J. H., & Richard, F. -J. (2013). Intracolony vibroacoustic communication in social insects. Insectes Sociaux, 60(3), 275-291. https://doi.org/10.1007/s00040-013-0311-9

Huang, L., Benites, D., Lyu, S., Smith, T., Li, M., Shang, Y., Klettner, C. (2019). UCL OpenFOAM Course Notes 2019. doi: 0.13140/RG.2.2.18118.83529.

Jackson, J. C., & Windmill, J. F. C. (2016). Mechanical Specializations of Insect Ears. In G. S. Pollack & A. C. Mason & A. N. Popper & R. R. Fay (Eds), Insect Hearing (pp. 125-157). Springer Cham. https://doi.org/10.1007/978-3-319-28890-1_6

Jadhav, S. P., Wolfe, J., & Feldman, D. E. (2009). Sparse temporal coding of elementary tactile features during active whisker sensation. Nature neuroscience, 12 (6), 792-800. https://doi-org.proxy3.library.mcgill.ca/10.1038/nn.2328

Jones, A. & Marshall, C.D. (2019) Does Vibrissal Innervation Patterns and Investment Predict Hydrodynamic Trail Following Behavior of Harbor Seals (Phoca vitulina)? The Anatomical Record 302:1837–1845. https://doi.org/10.1002/ar.24134

Knisely, S. (2011, Feb. 25). Insect hearing inspires new approach to small antennas. University of Wiscounsin News. https://news.wisc.edu/insect-hearing-inspires-new-approach-to-small-antennas/

Kubo, R. (1966). The fluctuation-dissipation theorem. Reports on Progress in Physics, 29(1), 255-285.

LibreTexts. (2022, Sept. 2). 18.11: The Equipartition Principle. LibreTexts Chemistry. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Physical_Chemistry_(LibreTexts)/18%3A_Partition_Functions_and_Ideal_Gases/18.11%3A_The_Equipartition_Principle

Lippsett, L. (2020, Sept. 16) How Seal Whiskers Track Prey Underwater: Harbor seal whiskers sense the wake left by swimming prey by cancelling out signals from the seal’s own movement.  Ask Nature. https://asknature.org/strategy/whiskers-sense-prey-movement/#introduction

Loudon, C. (2009, January 1). Chapter 6 – Antennae (V. H. Resh & R. T. Cardé, Eds.). ScienceDirect; Academic Press. https://www.sciencedirect.com/science/article/pii/B9780123741448000060

Muthuramalingam, M., Bruecker, C. (2019) Seal and sea lion whiskers detect slips of vortices similar as rats sense textures. Nature Scientific Reports 9 1–15. doi:10.1038/s41598-019-49243-5

Oladazimi, M., Brendel, W., & Schwarz, C. (2018). Biomechanical texture coding in rat whiskers. Science reports, 8 (1), 1-12. https://doi-org.proxy3.library.mcgill.ca/10.1038/s41598-018-29225-9

Römer, H. (2020). Directional hearing in insects: biophysical, physiological and ecological challenges. Journal of Experimental Biology, 223(14). https://doi.org/10.1242/jeb.203224

Sofroniew, N. J., & Svoboda, K. (2015). Whisking. Current biology, 25 (4), 137-140. https://doi.org/10.1016/j.cub.2015.01.008 

Types of insect antennae. (2019, April 11). Agri Learner. http://www.agrilearner.com/types-of-insect-antennae/

Wang, L. (2017, Sept. 26) Whiskers Reduce Drag: The highly sensitive whiskers of harbor seals reduce vortex-induced vibrations during swimming due to their undulating surface structure. Ask Nature, https://asknature.org/strategy/whiskers-reduce-drag/

Wieskotten, S., Mauck, B., Miersch, L., Dehnhardt, G., & Hanke, W. (2011). Hydrodynamic discrimination of wakes caused by objects of different size or shape in a harbour seal (Phoca vitulina). Journal of Experimental Biology 214, 1922-1930. doi:10.1242/jeb.053926

Wolfe, J., Hill, D. N., Pahlavan, S., Drew, P. J., Kleinfeld, D., & Feldman, D. E. (2008). Texture coding in the rat whisker system: slip-stick versus differential resonance. PLoS Biology, 6 (8), 1661-1677. https://doi.org/10.1371/journal.pbio.0060215 

Yu, Y. S. W., Bush, N. E., & Hartmann, M. J. Z. (2019). Whisker vibrations and the activity of trigeminal primary afferents in response to airflow. Journal of neuroscience, 39 (30), 5881-5896. https://doi.org/10.1523/JNEUROSCI.2971-18.2019

Yu, Y. S. W., Graff, M. M., & Hartmann, M. J. (2016). Mechanical responses of rat vibrassae to airflow. The Journal of experimental biology, 219 (7), 937-948. https://doi.org/10.1242/jeb.126896 

Zheng, X., Kamat, A.M., Cao, M., Kottapalli, A.G.P. (2021). Creating underwater vision through wavy whiskers: A review of the flow-sensing mechanisms and biomimetic potential of seal whiskers. Journal of the Royal Society Interface, 18 (183), art. no. 20210629. doi: 10.1098/rsif.2021.0629Zheng, X. Z., Kamat, A. M., Krushynska, A., Cao, M., & Kottapalli, A. G. P. (2022). 3D Printed Graphene Piezoresistive Microelectromechanical System Sensors to Explain the Ultrasensitive Wake Tracking of Wavy Seal Whiskers. Advanced Functional Materials, [2207274]. https://doi.org/10.1002/adfm.202207274