Functional Mechanics of the Elephant and Butterfly Proboscis
Han Ru Liu, Letizia Marello, Liam Sterne, Kori Zhang
Abstract
The trunk, also known as the proboscis, is a tubular, flexible and hollow appendage that varies in size and function; some species use it to regulate temperature, while others use it for feeding or grabbing. The purpose of this paper is to explore the biological mechanics of the movement and suction of the trunk in various species and to decompose their kinematic behaviors. These intrinsic behaviors help us understand more about non-rigid body dynamics. This paper focuses on two animals: elephants and butterflies. African elephants, like most mammals, have a musculoskeletal system. However, most discussion pertains to their hydrostatic features, namely the trunk. Models of the movement and forces acting upon the trunk during activity are explored to expand knowledge on the workings of these organs. Among insects, the feeding behavior of Lepidoptera is heavily dependent on their proboscis. When feeding is necessary, the proboscis leaves its resting position and undergoes an extension-recoil cycle. For both species, the proboscis is essentially used for drawing up different fluids. The analysis of the mechanism of the suction is therefore essential to understand one of the principal functions of the proboscis and how it applies to elephants' and insects' morphology.
Keywords: trunk, proboscis, movement, mechanics, kinematic behavior, extension-recoil cycle, suction, elephants, butterflies.
Introduction
Muscular hydrostats are incredible organs that differ from common musculoskeletal systems seen in mammals such as humans. They are exclusively composed of muscular tissue and do not rely on structural components such as bones and rigid cartilage. Hydrostatic skeletons rely on incompressible fluid-filled compartments that provide hydrostatic pressure to given cavities which maintain the shape of these hydrostats. One of the most important examples is without any doubt the trunk. Though muscular hydrostats such as the proboscis lack the fluid compartments, they rely on many of the same muscular antagonistic ideas which allow them to perform the vast array of capabilities they display. The proboscis is indeed used by animals in several different ways. The trunk of the African Elephant, for example, has the almost mystifying ability to rip large trees out of the ground and support over 250 kg of weight yet be able to pick up a tortilla chip without cracking it. It is the complex arrangement of muscles along the organ that allows it to complete such tasks. Though the proboscis in the elephant exhibits seemingly infinite kinematic mechanisms, it can be broken down into a finite set of motion primitives decomposed into fundamental curvature, torsion and strain measurements. This set of motion primitives can be equally applied to the proboscises found in insects, the butterfly in particular. Due to the repeated extension-coil cycle of the proboscis needed for feeding, butterfly proboscises apply a mix of muscular contractions, cuticular elasticity, and corrugated crack structure to reduce the strain caused by an optimized curvature. In addition, feeding habits of butterflies, as well as elephants, are also dependent on the suction that can be performed by the proboscis. Its mechanism functions through a pressure gradient which is made by different parts of the body depending on the skeleton and respiratory system of the studied species. This paper will focus on the movement, torsion and strain of the elephant trunk, the coiling and unfurling mechanisms of the butterfly proboscis, and finally, the common suction feature used for feeding in both elephants and butterflies.
Proboscis Movement
Kinematic variables and trunk anatomy
With thousands of muscles and immense brain power dedicated to the motion of the trunk, complex motion is an intrinsic part of the organ's behavior. The infinite degree of movement in which the trunk can move can be parameterized and simplified with some assumptions. Muscular hydrostats rely solely on muscle tissues and hydraulic movement rather than bones, tendons, and ligaments. This complex range of behaviors can be broken down into a series of finite movements. While the trunk itself is composed of over 40,000 individual muscles, three different orientations of muscles exist to provide specific behaviors (Dagenais et al., 2021). As shown in Figures 1 and 2, these three groups are the (1) muscles parallel to the long axis of the organ, (2) muscles perpendicular to the long axis, and (3) muscles oblique or helical to the long axis of the organ (Dagenais et al., 2021). The anatomy of the trunk is an intrinsic determining factor in the kinematic variables: strain, curvature, and torsion. Assuming the starting position of a long slender structure such as the trunk, the displacement of the structure can be modeled three-dimensionally from a set of scalar surface strain measurements.

Fig. 1 Longitudinal and oblique muscles arranged along the trunk.

Fig. 2 Cross section of African Elephant trunk: longitudinal (L), radial dorsal and ventral (rd, rv), and oblique deep and superficial (do, so) muscles.
Trunk displacement model from surface strain measurements
A local linearized solution approach is used as a basis for these strain models. The idea of a local linearized solution consists in the approximation of a multivariable function (F(x,y)) near one of its inputs with derivation. Then the tangent plane is analyzed at each input, which provides a function with the same value as the function at F and the same partial derivatives (Todd et al., 2017). This provides a source to determine the muscle groups applied for each curvature and deformation based on the muscle group being perpendicular to the plane on which the stress acts (Todd et al., 2017). This model can capture the set of kinematic variables which define the movement into scalar strain measurements and can assist in predicting its shape. The load-carrying tissue acts as a group with an overall stiffness that works to resist the load applied with incremental curvature, which assists in capturing maps of kinematic primitives for rudimentary tasks (Todd et al., 2017).
The rich repertoire of motor behaviors can be defined by the interactions between groups of muscles starting with elongation and contraction (Dagenais et al., 2021). Elongation and contraction are ubiquitous movements for the trunk when reaching for objects whether to eat, move, or manipulate. The basis for the movements of muscular hydrostats, like all muscles, is that of constant volume. Muscles work by sliding actin and myosin filaments and as the myosin filaments tighten up, the muscle fiber contracts. Considering the concept of constant volume, a decrease in one dimension will incite an increase in at least one other. Contraction among movements is one of the simplest. Contraction involves mainly two groups of muscles: perpendicular and longitudinal muscles (Dagenais et al., 2021). The marvelous speeds at which the trunk can elongate and contract is allowed by the coupled contraction of the longitudinal muscles which strain the hydrostat horizontally, while the perpendicular muscles stress the organ radially, increasing the diameter and simultaneously decreasing the length (Kier et al., 1989). However, assuming constant volume puts certain restraints on the behavior, which concludes that this assumption is not necessarily true.
Motion primitives
Elongation
Elongation, as one of the motion primitives, is a building block of the vast array of strategies elephants use to manipulate objects. Elongation is a similar motion to contraction; however, the radial muscles will loosen to reduce cross sectional area as the longitudinal muscles do the same to elongate axial length. The African Elephant was measured to have an impressive 135% elongation capacity between shortest and longest lengths of the trunk (Boyle, 2022). While the cross-sectional strain of the organ is directly related to the longitudinal strain of the muscles, connective tissues offer a surprising elastic potential to limit deformations and thus assist in passive elongation. The tissue is an elastic structure and therefore stores potential, which can have an acute effect on the muscles force and power. The elastic mechanism can help store the work of the contraction and release it much faster than the muscle tissue, which aids in the speed of elongation.
Figure 3 depicts the coordination of longitudinal and oblique muscles to provide support to load lifting in the trunk (Wilson et al., 1991). Different oblique lengths and angles characterize the muscles with those with greater helical angle than 54o contributing to elongation, and those less for shortening. There is no discrete definition of which muscles in the array of the trunk belong to longitudinal, oblique and radial groups; however, parameters defining them with their pitch respective to the neutral axis helps simplify models.
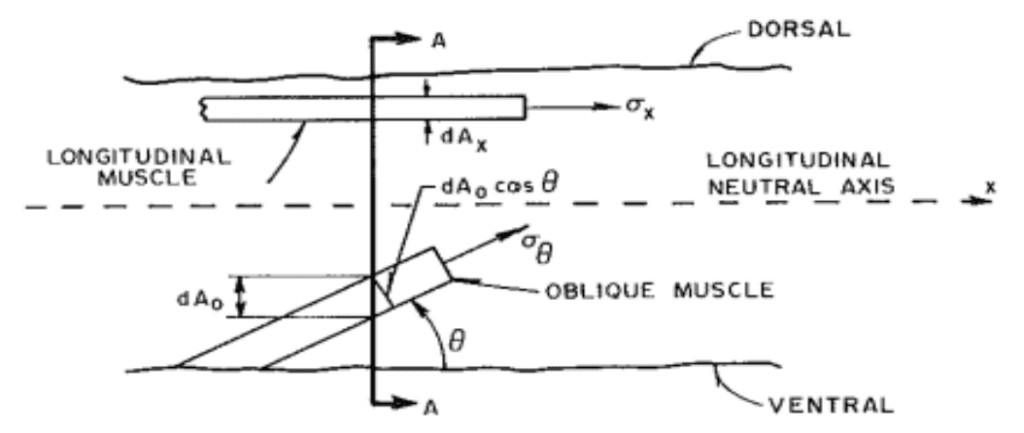
Fig. 3 Definition of stress orientation for a typical oblique muscle (Wilson et al., 1991).
The equilibrium of forces condition must be reached along the neutral axis while there are two main sources of strain. First, the change in trunk length causes a longitudinal stress and thus axial strain. The x-oriented components of oblique and longitudinal provide stress along the long axis of the trunk, as seen in Equation (1). Second, the y components contribute cross-sectional strain in elongation demonstrated by Equation (2) (Boyle, 2022). This transverse strain is a result of the stress on tissue perpendicular to the reach axis. The strains can be quantified with the following equations where ɛA is the axial strain, ɛT is the transverse strain, L and R are unstressed trunk length and radius and δL and δR the change in their values respectively.
\begin{equation}
\epsilon_A=\delta L/L
\end{equation}\begin{equation}
\epsilon_T=\delta R/R
\end{equation}Using the assumption of constant volume and linear radius change, (1) and (2) are used to determine a form of transverse strain as a function of axial strain and geometrical dimensions of the trunk (3) (Boyle, 2022). In the equation, c is a constant relating radii at two distances and r0, RL and rL the radii.
\begin{equation}
\epsilon_T=-\epsilon_A\left(\frac{1}{2}-\frac{r_0^2+r_Lr_0+r_L^2}{R^2_L\left(c^2+c+1\right)}\right)
\end{equation}The moment on the trunk in elongation in an assumed completely vertical position is initially zero. As the trunk begins to lift the load, it will not just rely on shortening but rather incorporate a twist or coil in an upward motion data from incremental distributed stress and strains; the apparent stiffness quantity describes the moment, knowing the radius of curvature. The apparent stiffness with sufficient anatomical and geometrical data can be calculated as a function of the linear relationships of incremental x forces on longitudinal and oblique muscles and y moment arms (Wilson et al., 1991). Using this stiffness, stress and strain of cross-sectional segments of the hydrostat can be determined. The rather narrow range of data presented for the stress on separate muscle groups supports the theory that the trunk acts as a beam for classical beam theory with distributed tension, compressions and a neutral axis (Wilson et al., 1991). This is because of the assumptions made in the theory that the material has a homogenous cross-section, there is no deformation in the plane cross-section and bending forces do not exceed the elastic limit (Wilson et al., 1991).
Elongation anomaly
One major flaw in previous hydrostat elongation theory is that uniform elongation does not apply to elephant trunks. Considering the extraordinary volume of muscle in the comparatively large organ, the telescoping elongation may be a result of the tapering of the trunk (Boyle, 2022). Segments with lower volume will require less work and because the elephant may conserve energy expenditure it will only use the amount of energy needed to extend each segment. Others also explore the unique property in the elephant's skin that accounts for this elongation asymmetry. Stretchier skin on the dorsal side helps with their telescoping extension downwards to its target as well as providing a shield to natural elements. The ventral side that is less elastic but more ribbed can aid in gripping and will not bulk as the trunk coils (Schulz et al., 2022). This is complemented by the asymmetry in dorsal ventral elongation patterns for the female African elephant. Along with the chameleon tongue, the trunk has a unique arrangement of helical and perpendicular muscles that are not consistent throughout the cross-section of the trunk, which may contribute to the non-uniform elongation behavior of both species. Figures 4 and 5 depict the potential effects of the non-homogenous oblique muscle distribution (Boyle, 2022). The oblique muscles, only ventrally located, are a probable cause of the imbalance of strain as they will cause a stronger ventral contraction straining the dorsal, less elastic side of the trunk.
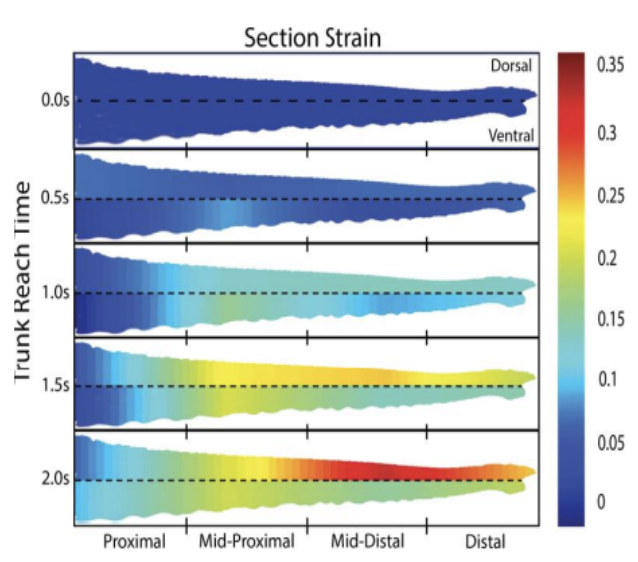
Fig. 4 Sectional strain depicted by heat maps indicating increasing strain along intervals of the trunk during elongation.
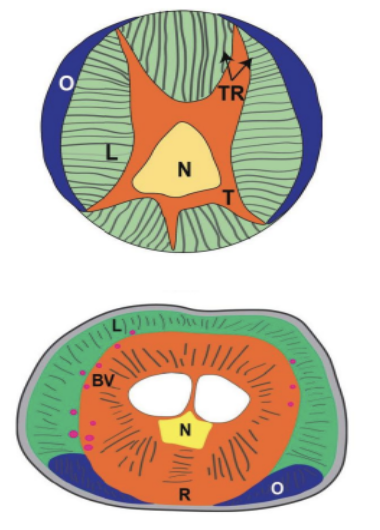
Fig. 5 Contrast of octopus tentacle (top) and elephant trunk (bottom) muscular distribution.
Bending and torsion
These motion decompositions create a striking image for the variety of techniques the elephant will employ when maneuvering objects with its trunk. The most common motion observed is that of the distal wrap for cylindrical-shaped objects which requires trunk curvature. Torsion and bending are now explored in this technique employing a whole new set of variables in motion (Kier 1985). The anatomy of the proboscis allows for this necessary behavior with perpendicularly arranged muscle groups and radially, peripherally located longitudinal muscles. Bending requires a unilateral contraction of longitudinal muscles yet must maintain constant diameter so as not to cause a contraction in the entire organ, as shown by Figure 6 (Kier, 1985).

Fig. 6 The contrast between constant and varying diameter for bending motion (Kier 1985).
The resistance provided by activity of the helical/oblique and perpendicular muscles will ensure bending with constant diameter antagonistic to the contractile longitudinal activity. Finally, torsion works through helical muscle contraction which contributes to the twisting of the tip relative to the base of the drunk. Similar to the longitudinal muscles in bending, peripherally located helical muscles are more efficient at causing a moment arm and thus greater torque (Kier, 1989).
Model discrepancies and auxetic behaviour
Moreover, there is controversy surrounding the concept of volume conservation and whether the trunk truly behaves in this fashion. Auxetic behavior is a counterintuitive approach to modeling elongation and contractile behavior of hierarchically organized structures (Yang, 2004). With a system of over 4000 muscles within the trunk, simple constant volume assumptions simplify motion models but restrict ideas of the freedom of the organ. Treating the organ as one large component with cooperating groups of muscles is a surface-level understanding of dynamic interactions in biological systems. Therefore, the theory of biotensegrity revolutionizes the incalculable amount of cooperation between all components of an anatomical construct. Auxetic structures have a negative Poisson ratio, a ratio that defines the change in transversal dimensions as a result of axial strain, and vice versa (Yang, 2004). It demonstrates the behavior of typical deformable materials that deform in directions perpendicular to applied loads. However, auxetic structures behave oppositely by expanding in directions parallel to loads; thus, when stretched in one direction, will stretch in all directions.
This theory is explored for large hierarchical muscle systems because of the tensegrity approach to their anatomy. Mathematical analysis of such structures is incredibly complex because of the divergence from classical mechanics. A continuum model of the muscle tissues and fascial system within the trunk looks at how an array of elements can more comprehensively describe the motion (Scarr, 2019). The incorporation of fluid mechanics with liquid phase fascia and non-connective tissues such as blood and lymph add further depth to the anatomical level tensegrity model (Bordoni, 2018). Figure 7 is a sample biotensegrity web of interaction in a biological system with a hierarchical RAIN model: Rapid Adaptability of Internal Network. Ultimately models cannot be restricted by discrete comprehensible simplifications of immensely complex structures such as the trunk. Tensegrity and auxetic behaviors incorporate more than a subset of mechanisms that work together for a functioning unit. It accounts for the dynamic interactions between the smallest subunits and living tissues and complex morphology or biological architecture. However, assumptions must be made to understand fundamental behaviors before opening up to tensegrity perspectives of stress-strain relationships to the mechanics of the trunk.
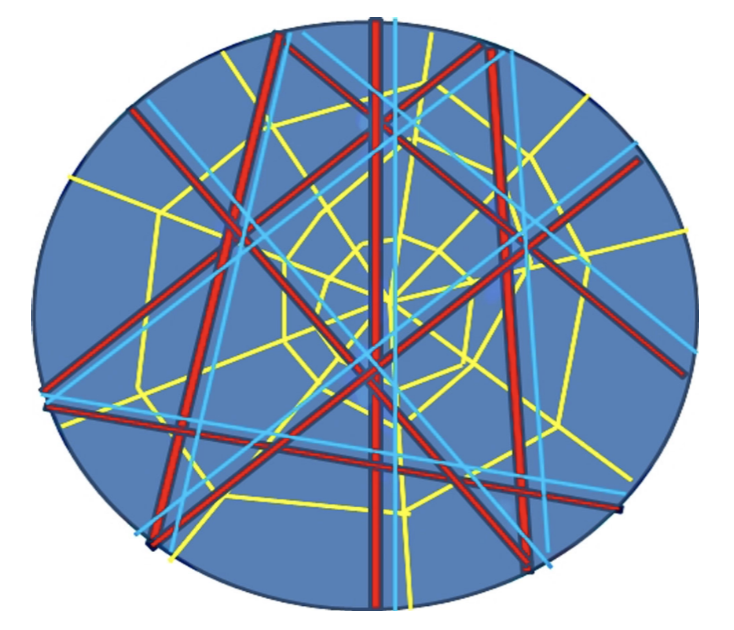
Fig. 7 RAIN model. The web of red, blue and yellow lines depicts the muscles and bones, vascular and lymphatic systems and indissoluble connective fascial layers. The surrounding black circle is the epidermis closing the body with blue liquid components contained.
Though elongation, bending and torsion are vital to the movement and utility of the trunk, many smaller scale behaviors are what fascinate researchers. The gentle grip with the tip of the trunk and method of suction lifting are what allow delicate maneuvers. Elephant trunks are one of the many muscular hydrostats that are commonly explored in research for soft robotic developments. Bioinspired devices rampage the market and the ideas of a lack of stiff skeleton allow for more versatile properties. The functions of trunks are more concentrated on movement and collection of food whereas other animals such as insects have proboscis as a main source of feeding. With many similar motions and muscular adaptations, insects have remarkable abilities to coil and relax which the elephant does not employ as much.
Proboscis folding
Hydraulic mechanism for Lepidoptera proboscis unfurling
In a similar fashion to the elephant trunk, insects utilize an elongated and tubular structure termed proboscis. In insects, this organ constitutes the sole feeding mechanism, acting as a canal to take up liquid food. Among the class Insecta, butterflies possess a remarkably long and flexible proboscis which is used as a straw for sipping nectar. The Lepidoptera proboscis is coiled into 4-5 turns in the resting position and is attached to the rest of the body cavity via the stripes. Coupled by a series of dorsal and ventral legulae, this food canal comprises two elongated maxillary galeae (Fig. 8) (Zhang et al., 2021).

Fig. 8 The proboscis morphology. a) General interior view, b) dorsal view, c, d) lateral view. DL, dorsal legulae; FC, food canal; Pi, pilifer; VL, ventral legulae (Zhang et al., 2021).
When feeding is required, the tightly coiled spiral of the proboscis is released by reflex; when the butterfly lands on a good food source, the taste organs at the end of its legs help initiate this reflex (Wilson, n.d.). The reflex initiates the contraction of the muscle closest to the head, the basal galea muscle, which unlocks the coil from its spiral position and allows it to unfurl (“Proboscis Unwinds,” 2016). The proboscis is initially unfurled with the help of the proboscis' elasticity, which tends to uncoil when not held in its resting position, but the full unfurling of the proboscis is done by muscle contractions and the hydraulic mechanisms of the stipe valves.
The uncoiling process of the Lepidoptera proboscis is heavily dependent on changes in hydraulic pressure. After the proboscis is elevated by the basal galea muscle, the basal maxillary segment of the proboscis, the stipe muscles, contracts and compresses the stipital tube (Krenn, 2010). As the proboscis is drawn upwards, the stipe valves close and the tubular part of the stipes effectively becomes a closed cylinder (Schmitt, 1938). After repeated compressions of the stipes, hemolymph is pumped into the galea and pressure is exerted against the blood of the stipital tube. This generates a pressure gradient that continues to move outwards through the stipes, raising the proboscis and consequently leading to its stepwise uncoiling (Fig. 9) (Krenn, 2010).
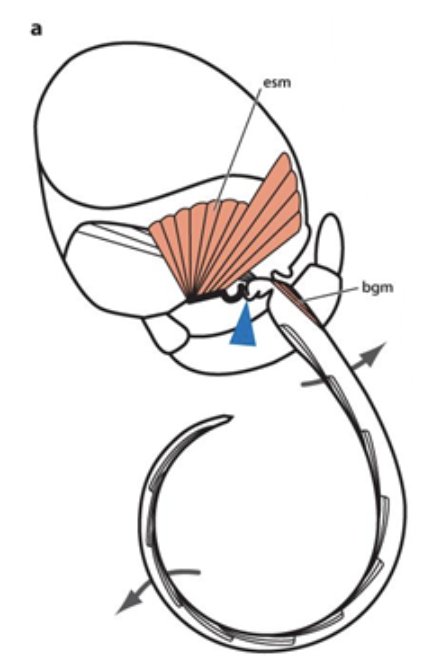
Fig. 9 Hydraulic mechanism of proboscis uncoiling (Krenn, 2010). The blue arrowhead corresponds to the stipital tube compressed by external stipes musculature (esm); basal galeal muscle (bsm) elevates the proboscis.
As the internal pressure of the galea increases, the dorsal wall arches outwards and generates a change of shape of the proboscis. The flexibility of the Lepidoptera proboscis allows it to alternate easily from a coiled bent position to a nearly straight posture when fully unfurled (Krenn, 2010). The extension-recoil cycle continues as the stipe valves reopen; the muscle contractions and cuticular elasticity enable the recoiling of the proboscis (Hepburn, 1971).
Capillary force and the function of saliva in proboscis folding
Proboscis folding involves a cycle of repetitive extension and coiling, often accompanied by saliva droplets. Saliva is discharged between the galeae when required by the Lepidoptera, which helps bridge the galeae together during these processes. A muscular pump directs the release and retraction of saliva, which moves back and forth along with changes in proboscis coil radius (Fig. 10) (Zhang et al., 2018).

Fig. 10 Saliva drop release between two separated galeal strands during proboscis assembly (Zhang et al., 2018).
According to several observations, the saliva column formed between the galeae facilitates the assembly of the proboscis. When the galeae start to separate, a comparison between the proboscis coil radius and the intergaleal distance reveals that the former is much larger than the latter. Thus, the galeae can be considered as straight parallel beams pulled together by a capillary force f acting per unit length of each galea (Fig. 11 and 12) (Zhang et al., 2018).
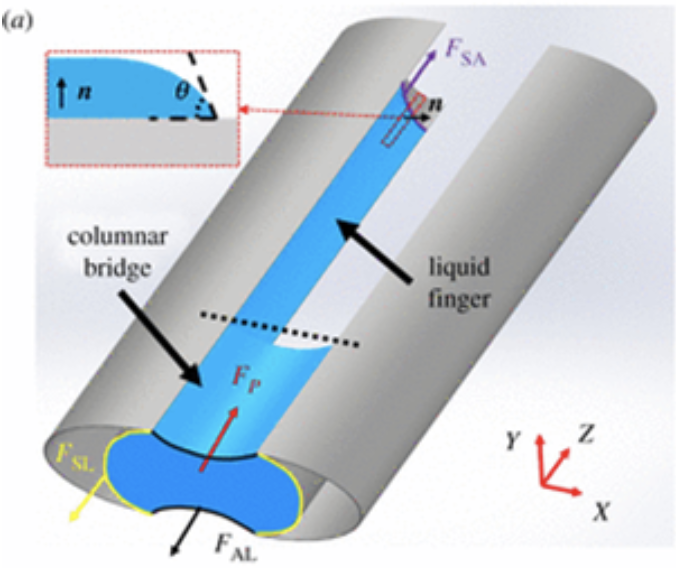
Fig. 11 a) The shape of the columnar bridge of saliva formed between two separated galeae (Zhang et al., 2018).

Fig. 12 e) Schematic of the cross-sectional shape of a saliva bridge with concave menisci; f) schematic of the cross-sectional shape of a saliva bridge with convex menisci (Zhang et al., 2018).
This capillary force can be determined using the following equation:
f=2\sigma u\left(\frac{d}{r}\right)In Equation (4), σ represents the surface tension of saliva measured in N/m, 2d represents the spacing between the two galeae, r represents the radius of the food canal, and u(d/r) represents a function solving the Laplace problem of capillarity.
Coiling mechanisms: muscle groups
The proboscis of insects is unique to all other trunks because it is coiled in a tight spiral near the head while in a resting state. This feature is especially useful for species of the Lepidoptera order, including butterflies and moths, that have proboscises of extraordinary lengths and need to hop from one flower to the next for feeding.
The initial coiling process involves the valve-like structure of the stipes. In order to unfurl the proboscis, a pressure gradient in the stipes is used in a stepwise mechanism; the stipes must, therefore, release their increased internal pressure by opening before the proboscis can be coiled. Because the proboscis is coiled and uncoiled constantly to feed, the material of galeal walls and its elasticity make it so that the food canal is not deformed during the coiling and uncoiling processes (Krenn, 2010). After the release of the internal pressure, the main coiling mechanism of the proboscis involves the contraction of the intrinsic galeal muscles and the internal stipe muscles, and although the placement of these muscles slightly varies between species, it has been found that the fundamental coiling mechanism is independent of muscle arrangement (Fig. 13) (Krenn, 1990).
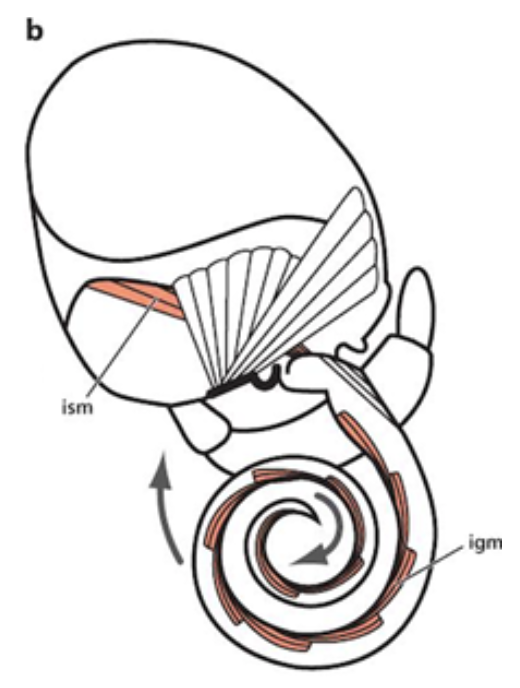
Fig. 13 Placement and contraction of the internal stipe muscles (ism) and the intrinsic galeal muscles (igm) during the coiling process of a Lepidoptera (Krenn, 2010).
In addition, the elasticity of the proboscis also helps to ensure that the proboscis slightly coils from the unfurled position without the help of the muscles. However, this same elasticity tends to uncoil a tightly coiled proboscis from its resting state. Once the proboscis is coiled tightly, with no space left between the coils, it lies near the head between the labial palps; the elasticity of the proboscis allows it to unfurl until it is propped under the head. However, other mechanisms, known as cuticular processes, are needed in order to conserve energy and maintain this position for long periods of time without tension or muscle exertion. Cuticular processes, known as legulae, are scale or hair-like structures that are found on the proboscis of all Lepidopteran species, except the Sphingidae. These cuticular processes are present on various different areas of the proboscis depending on the species; it is at least found in the galeal areas that are in contact while in the coiled position, but some species have cuticular processes on the ventral side of the head, or on the lateral walls for additional support. These structures are interlocked between each coil in various directions, creating a large frictional effect like interlocking pages of two books or bristles of two brushes (Fig. 14 and 15) (Krenn, 1990).

Fig. 14 SEM images of a tightly coiled proboscis of a Mamestra brassicae with interlocking cuticular processes (cp) (Krenn, 1990).

Fig. 15 SEM images of both scale and hair-like cuticular structures on the dorsal side known as dorsal legulae (dl) (Lehnert et al., 2015).
Without too much muscle strain and tension, the combination of a spring-loaded proboscis with its interlocking cuticular processes help Lepidoptera conserve energy and maintain the resting position.
Coiling mechanisms: stress reduction and large curvature (Chen et al., 2020)
Many instances of folding exist in nature, from protein folding to the folding of bird wings during perching. However, an impressive large curvature folding pattern is found in the semi spring-like elastic structure of a butterfly proboscis, with an extraordinary coiled to uncoiled length ratio varying between 1:8 and 1:15; folding such a thick trunk into such a compact structure requires some specific strategies, including a flexible strain storage strategy, a smaller modulus of elasticity in the internal features of the proboscis as compared to the external, and most importantly, a corrugated crack structure.
When observed under a microscope, it was found that the thickness, width and the folding curvature were not uniform throughout the proboscis length; both the thickness and width were found to increase gradually from the tip to the base of the proboscis near the head, whereas the folding curvature was found to decrease from the outside to the inside (Fig. 16 and Fig. 17). It is precisely this conical structure that effectively reduces the stress and strain on the proboscis that is needed to accommodate the large curvature during storage, and the constant coiling and uncoiling.

Fig. 16 Decreasing folding curvature from outside to inside of a Golden silk cat butterfly (Polyura eudamippus) (Chen et al., 2020).
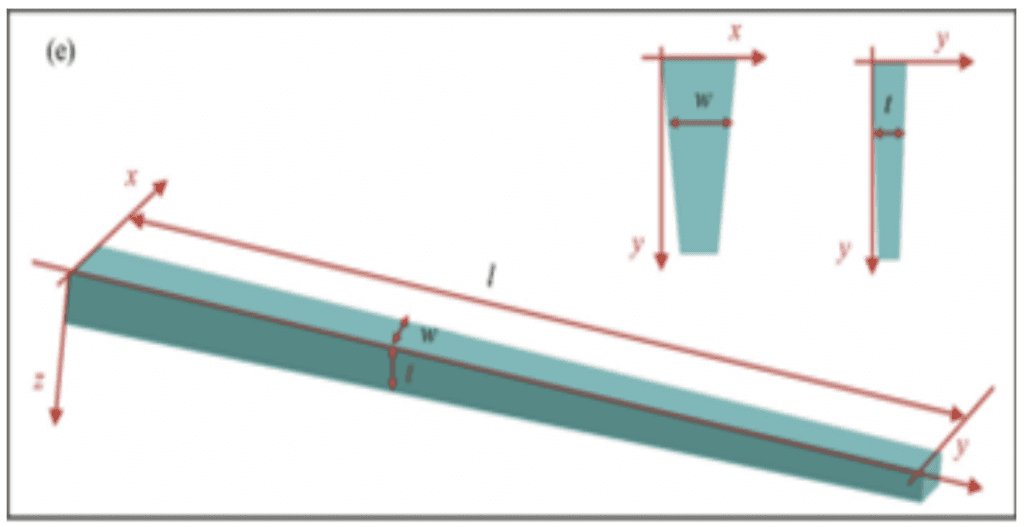
Fig. 17 Modeled conical structure of a stretched proboscis where width (w), thickness (t) and length (l) are shown (Chen et al., 2020).
As previously mentioned, the proboscis is an elastic structure; it is precisely this elasticity that helps in unfurling and recoiling. The specific elasticity and hardness of the proboscis structure was measured by nanoindentation, a probing technique used on a small scale to test mechanical properties of materials, using 9 points forming a rectangular area, and 9 points forming a line (Fig. 18, 19, 20 and 21).
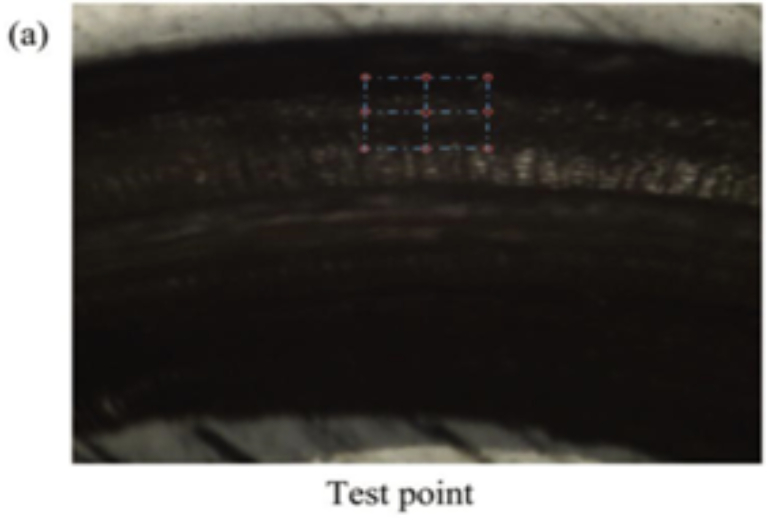
Fig. 18 The rectangular area test points used in the nanoindentation of a butterfly proboscis (Chen et al., 2020).

Fig. 19 The straight line test points used in the nanoindentation of a butterfly proboscis (Chen et al., 2020).

Fig. 20 Nanoindentation force-displacement curves at 4 μm indentation depth for the rectangular area test points (Chen et al., 2020).
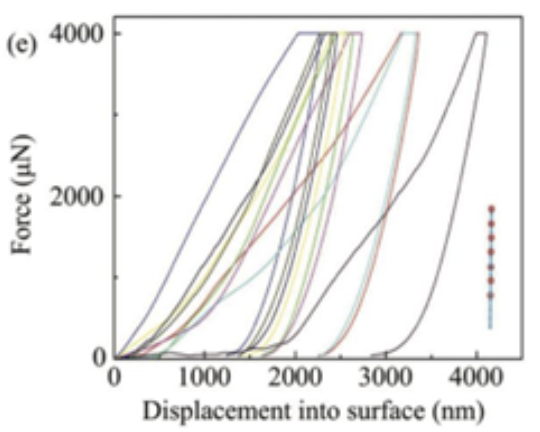
Fig. 21 Nanoindentation force-displacement curves at 4 μm indentation depth for the straight line test points (Chen et al., 2020).
The measured elastic modulus and hardness of the proboscis material varied greatly between the different test points. The elastic modulus varied from 0.25 to 1.3 GPa, and the hardness varied between 0.01 and 0.2 GPa with the rectangular area test points. On the other hand, the elasticity varied from 0.38 to 0.8 GPa, and the hardness from 0.01 to 0.1 GPa with the straight-line test points; this large range obtained indicates that the proboscis is composed of complex materials. The exoskeleton was found to be the part of the proboscis with the highest elastic modulus and hardness in those ranges; this makes sense as the exoskeleton covers the surface of the proboscis and must protect it from wear, especially from the constant stretching and recoiling and any external environmental factors, such as acidic liquids that it may encounter to find a good food source. The main materials of the proboscis exoskeleton were speculated to be chitin and resilin, as these materials are great with anti-fatigue and anti-corrosion properties. The area with the lowest elastic modulus was found to be in the cellular tissues, including trachea, nerve and muscle tissue. It is precisely this combination of hard and elastic external but soft internal features that allows the butterfly to achieve such a large folding curvature without too much stress; having too much elasticity and hardness would prevent it from easily folding, but the presence of the internal softer less elastic tissue counterbalances this effect and lowers the overall elastic modulus and hardness.
Finally, the most important feature found on the proboscis allowing it to achieve such a large folding curvature is its corrugated crack structure. Using a Field Emission Scanning Electron Microscope (FESEM), the microstructures of the butterfly proboscis were shown to be lined by a dense corrugated crack structure. The length and distribution of these corrugated cracks along the proboscis were found to vary. Some cracks were found to run radially through the whole proboscis surface with a length of up to 250 μm, whereas others had a gap of only 50 μm (Fig. 22 and 23). However, the consensus and general trend is that the larger the curvature, the larger the number of corrugated crack structures (Fig. 24).

Fig. 22 Distance between two crack structures (D) (Chen et al., 2020).

Fig. 23 Gap size (d) (Chen et al., 2020).

Fig. 24 SEM image of the density of a crack structure in small versus large curvature areas (Chen et al., 2020).
Through SEM imaging, the crack structures at different areas were neither seen to be rectangular nor V-shaped, but an irregular pattern of different shapes and arcs was observed (Fig. 25); this irregular curved structure without acute angles reduces the concentration of stress in areas of the proboscis.
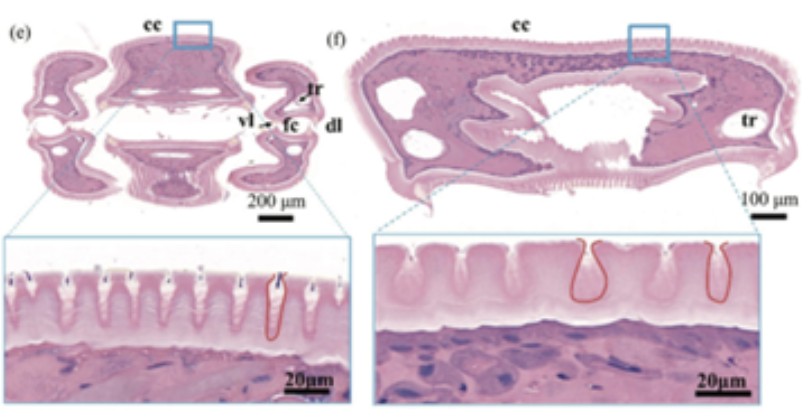
Fig. 25 Tissue section of the proboscis demonstrating irregular crack structures (Chen et al., 2020).
Although the crack structure of each individual gap is different and varies between areas, the arrangement of the cracks is regular; this means that the proboscis is able to accommodate strain in multiple different directions, including the bending direction and the direction perpendicular to the bending. A modeled version of the strain on a bent proboscis was produced (Fig. 26).

Fig. 26 Model of a bent proboscis induced by a compression force (Chen et al., 2020).
In summary, the butterfly proboscis applies three main strategies to reduce stress exerted on the proboscis and be able to achieve such a large folding curvature every time it bends into its resting position. The conical shape and non-uniform width and thickness of the proboscis, as well as the elastic modulus and hardness structures in the proboscis, allow it to experience minimal strain and maximum curvature. However, the most significant and interesting structure in the proboscis studied is the corrugated crack structure that allows it to bend in multiple directions while reducing strain concentration. By using 3D and 4D printing to replicate the extraordinary strategies and phenomena of the butterfly proboscis, the state-of-the-art can progress to create rolled electronics and flexible robots.
Proboscis suction
Mechanism of the suction
One of the most useful and important functionalities of the proboscis is also the ability to take up various fluids like water, honey, blood, etc. It is extremely interesting to analyze the mechanism of the suction of the trunk, especially in insects, where the trunk is a crucial feeding apparatus, proved by the presence of various muscles and techniques used for unfurling that can be observed in butterflies, as previously explained.
The feeding habits of butterflies, and more generally those of insects, are highly related to the size, structure and function of their proboscis. The capacity of this apparatus can be measured by analyzing the volume of fluid uptaken by the species during a feeding experiment. For example, nymphalid butterflies can ingest a volume ranging from 36 to 133 µl of artificial nectar depending on their body size whereas tropical moths consume between 0.4 g and 1 g of nectar per night. Surprisingly, the moth can pump an equivalent of 12% of its body mass per minute which represents more than 600 times its body mass in 3.4 h. The viscosity of the fluid taken by the species also influences the quantity that the insect will suck up. For instance, the meal size of tropical moths decreases linearly with increased sugar concentration in the fluid, from 0.35 g with 10% of sugar concentration to 0.11 g with 50% (Krenn H. W., 2010).
How can we explain these relations and what exactly is the mechanism of suction?
Suction describes the air pressure differential between areas: when the pressure is reduced in one part of the physical system relatively to another, the fluid in the higher pressure region of the system will exert a force relative to the lower pressure region called pressure-gradient force. This pressure differential or pressure drop is therefore limited by the external pressure. Taking the example of a drinking straw: if the tip of the straw is in a liquid and the air in the straw is sucked, the air inside is removed creating negative pressure which will cause a pressure differential or imbalance between the external air pressure applied on the fluid and the lower pressure inside the straw pushing on the fluid. This imbalance causes more fluid to be pushed into the straw until the pressure created by the fluid column inside the straw is equal to the pressure difference (Fig. 27, Tech Science, 2021).
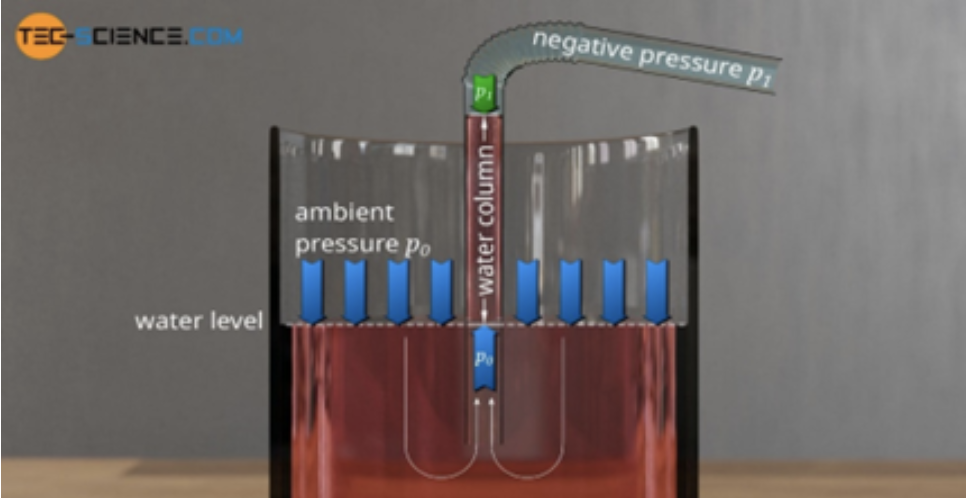
Fig. 27 Model of the mechanism of suction in a drinking straw (How Does a Drinking Straw Work?, 2021).
Suction applied to butterflies
Depending on the species, the pressure difference is created in different ways. The Glossatan Lepidoptera, like many insects with a proboscis, take up fluids in their proboscis along a pressure gradient that is created by a sucking pump in the head. The majority of their head muscles are associated with the sucking pump and form a functional complex with the proboscis: the sucking pump is an expandable cavity located between the proboscis and the esophagus. It has valve structures and the fluid transport is achieved by the closure of a posterior valve and the contraction of head muscles like dilators, compressors and sphincter which expand the sucking pump like a piston does in a syringe. This expansion reduces the pressure relative to atmospheric pressure, which forces the fluid to flow up the tube of the proboscis and enter the cranial pump (Fig. 28, Kornev et al., 2017).

Fig. 28 Micro-CT images of the Nadata gibbosa moth showing the position of the sucking pump complex in the head (Kornev et al., 2017). a) is the lateral view, b) the dorsal view, c) the anterior view. “An”: antenna, “Bu”: buccal chamber, “Co”: compressor, “Di”: dilators, “Es”: esophagus and “Pr”: proboscis.
The mechanical action of the pump is represented in the Bennet-Clark-Daniel-Kingsolver model (Figure 29). It has all the necessary characteristics to analyze the mechanics of the suction and liquid flow through the proboscis. In this model, the chamber floor and roof are assumed to be flat and rigid, so that the chamber or suction pump is a cylinder with a rectangular or circular cross-section.

Fig. 29 a) Daniel-Kingsolver model of the sucking pump (Kornev et al., 2017). The buccal chamber (Bc) has a cylindrical shape and when the plunger (Pl) moves in the vertical direction, it changes the expansion h of the buccal chamber . The proboscis (Pr) and esophagus (Es) are attached to the buccal chamber. b) The Bennet-Clark model of a sucking pump. The buccal chamber has a rectangular shape.
Considering the food canal in the proboscis as a cylindrical tube, as stated in the Bennet-Clark model, the flow of the fluid through the proboscis tube can be modeled too, by what is called the Hagen-Poiseuille flow. This model states that pressure through the cross-section of the proboscis tube does not change, therefore, the pressure at the entrance of the buccal chamber must be equal to the pressure in the proboscis leading to the following equation:
\begin{equation}
P=P\:p(t)
\end{equation}Moreover, if the position of the plunger as a function of time h(t) is known, as well as the pressure at the entrance of the buccal chamber Pp(t), then the model, also known as the drinking straw model, can describe the flow in the pump chamber.An interesting fact is that, through some computations, it can be proved that the function h(t) and Pp(t) are related: pressure generated at the opening of the buccal chamber is proportional to the rate of volume expansion of the pump chamber. Taking the same rate of expansion, the larger the chamber area, the greater the suction pressure. A smaller pump indicates, therefore, less suction pressure which will result in a shorter proboscis so that the insect does not need to combat friction forces that come with the fluid transport through a long proboscis. On the contrary, a greater proboscis volume will indicate a stronger pump (Kornev et al., 2017).
Suction applied to elephants
The mechanism discussed in the previous part is restricted to insects, but what about other animals that have different respiratory systems? The elephant, for example, does not have the same physical characteristics as the insects but can still make the pressure gradient needed for the suction to happen and suck up fluids like water to spray in their mouth, body, or air, or to grab objects. The proboscis is vital for them: as discussed above, the hydrostat has a wide range of muscles that allows several movements. Their proboscis also has an incredible capacity: they can hold 8.5 L of water in their trunk for example (Schulz et al., 2021). Their suction mechanism is very powerful but also surprisingly precise: elephants can blow air to push objects that are just beyond reach and modulate the air jet on a wall to draw objects closer to themselves. They can also use their trunk as a snorkel when traversing deep water.
To generate the pressure gradient for the fluid to flow up the proboscis, elephants have a similar mechanism to moths or butterflies, with an expandable cavity that will cause a pressure drop. Elephants have indeed strong diaphragm and muscles around the rib cage which contract, causing a change of volume in their lungs. This change leads to an increase in volume of the chest cavity which decreases the pressure inside, creating an imbalance with the external air pressure, resulting in suction through the proboscis (Fig. 30, Schulz et al., 2021).

Fig. 30 a) Side view of an elephant sucking up water (Schulz et al., 2021). Highest speed flow at the points closest to the nostrils. Scale bar: 5 cm. b) Bottom view of elephant sucking up water. Last picture shows the trunk closing to hold water. Scale bar: 3 cm. c: Schematic of an elephant trunk applying suction to an object of mass mt. The red arrows indicate the direction of flow. P0 is the pressure generated by the nostrils which leads to a flow u0 in the proboscis which decays with distance L.
However, elephants generate suction not only by using their lungs but also by increasing the diameter of their nasal volume. They can dilate their nostrils at a radius of nearly 30% and increase their nasal volume by 64%. All these characteristics make the suction very powerful: they can inhale at over 150m/s (or 490 ft/s) which represents around 30 times the speed of a human sneeze (Schulz et al., 2021). This high air velocity is also possible because of the specialized respiratory system of elephants. Their lungs are loosely connected to the chest walls by collagen fibers, which allows more ample lung-chest movements.
The study of the proboscis and its use for suction and feeding has inspired many biomimetic devices and technologies such as biphasic microneedle devices that mimic the insertion mechanism of the endoparasite proboscis to develop a more effective skin insertion and surface adhesion, which would be useful to lessen pain when inserted in the skin (Pooyan et al., 2022). Another example can be found in soft robotics, a rapidly developing field that has been exploiting biomimetic design principles. The strong yet simultaneously precise suction mechanism of an elephant trunk has greatly influenced the development of suction-assisted devices that can create a vacuum both above and below water.
Conclusion
Ultimately, the trunk, otherwise termed the proboscis, is a remarkable muscular hydrostat among many insect and mammalian species. This paper provides insight into the mechanics of the proboscis in elephant and butterfly species. In African elephants, the demonstrated complex trajectories and dynamic behaviors can be studied with simple motion decomposition into fundamental kinematic variables. The organ displays many different behaviors adapting to the object it aims to manipulate as a result of its muscular anatomy. However, simple decomposition limits the depth of analyses, and more dynamic models are also proposed. In Lepidoptera, the natural flexibility of the proboscis allows it to unfurl and coil repeatedly for the purpose of feeding. The insect's saliva secretion facilitates the assembly of the proboscis, allowing the organ to function properly as the animal takes up liquid food. A hydraulic mechanism, produced from a hemolymph pressure gradient, directs the extension of the proboscis. Furthermore, while the contraction of certain muscle groups certainly plays a role in the coiling and uncoiling of the butterfly proboscis, the many stress-reducing techniques, including a unique corrugated crack structure to allow for a large curvature with reduced muscle strain, as well as the interesting cuticular processes, are really the main components that allow the butterfly proboscis to stay coiled so compactly while searching for a good food source. In both the elephant and butterfly species, the ability to take up fluids is also governed by an incredibly useful suction mechanism. Due to the generation of a pressure gradient, the fluid is sucked up in the tube of the proboscis to allow the species to feed, in the case of insects, or, for elephants, to hold water to spray afterwards in the mouth, for example. This pressure gradient is generated differently depending on the physical characteristics of the animal: the butterfly uses the suction pump complex in its head while the elephant takes advantage of its powerful lungs and expandable chest cavity. However, the suction relies fundamentally on the same mechanism: an expandable cavity which will create pressure differential by expanding thanks to adjacent muscle contractions. There is no doubt that the study of the elephant trunk mechanics and movement is important to technological developments, as seen with the robotic arms that were developed after having studied the wide range of motion and gripping abilities of the elephant trunk. However, the more recently studied butterfly proboscis and its flexibility, hydrostatic mechanisms and size might also allow for future developments in micro or nanofluidic devices.
References
Bordoni, B., Marelli, F., Morabito, B., Castagna, R. (2018). A New Concept of Biotensegrity Incorporating Liquid Tissues: Blood and Lymph. Journal of Evidence-Based Integrative Medecine, 23. https://doi.org/10.1177/2515690X18792838
Boyle, M.A. (2022). The Biomechanics of Trunk Elongation.
Schulz, A.K., Boyle, M.A., Boyle, C., … & Hu, D.L. (2022). Skin wrinkles and fold enable asymmetric stretch in the elephants trunk. Proceedings of the National Academy of Science, 119(31), e2122563119. https://doi.org/10.1073/pnas.2122563119
Chadha, M., & Todd, M.D. (2017). A Generalized Approach for Reconstruction the Three-Dimensional Shape of Slender Structures Including Effects of Curvature, Shear, Torsion and Elongation. Journal of Applied Mechanics, 84(4), 041003-1 – 041003-11. https://doi.org/10.1115/1.4035785
Chen et al. (2020). Large Curvature Folding Strategies of Butterfly Proboscis. Journal of Bionic Engineering, 17, 1239-1250. https://doi.org/10.1007/s42235-020-0089-1
Dagenais, P., Hensman, S., Haechler, V., & Milinkovitch, M.C. (2021). Elephants Evolved Srategies Reducing the Biomechanical Complexity of Their Trunk. Current Biology, 31(21), 4727-4737. https://doi.org/10.1016/j.cub.2021.08.029
Hepburn, H. R. (1971). Proboscis extension and recoil in Lepidoptera. Journal of Insect Physiology, 17(4), 637-656. https://doi.org/10.1016/0022-1910(71)90114-4
How does a drinking straw work? (2021, April 12). Tec-science. Retrieved October 2, 2022, from https://www.tec-science.com/mechanics/gases-and-liquids/how-does-a-drinking-straw-work-principle-maximum-suction-lift/
Kier, W.M., & Smith, K.K. (1985). Tongues, tentacles and trunks: the biomechanics of movement in muscular-hydrosts. Zoological Journal of the Linnean Society, 83(4), 307-324. https://doi.org/10.1111/j.1096-3642.1985.tb01178.x
Kier, W.M., & Smith, K.K. (1989). Trunks, Tongues and Tentacles: Moving with Skeletons of Muscle. American Scientist, 77(1), 28-35. https://www.jstor.org/stable/27855549
Kornev, K. G., Salamatin, A. A., Adler, P. H., & Beard, C. E. (2017). Structural and physical determinants of the proboscis-sucking pump complex in the evolution of fluid-feeding insects. Scientific reports, 7(1), 6582. https://doi.org/10.1038/s41598-017-06391-w
Krenn, H. W. (1990). Functional Morphology and Movements of the Proboscis of Lepidoptera (Insecta). Zoomorphology, 110, 105-114. https://doi.org/10.1007/BF01632816
Krenn H. W. (2010). Feeding mechanisms of adult Lepidoptera: structure, function, and evolution of the mouthparts. The Annual review of entomology, 55, 307–327. https://doi.org/10.1146/annurev-ento-112408-085338
Lehnert et al. (2015). Structure of the Lepidopteran Proboscis in Relation to Feeding Guild. Journal of Morphology, 277(2),167-182. https://doi.org/10.1002/jmor.20487
Proboscis unwinds – biological strategy – asknature. (2016). AskNature Proboscis Unwinds Comments. https://asknature.org/strategy/proboscis-unwinds/
Pooyan et al., (2022). Bioinspired microneedle patches: Biomimetic designs, fabrication, and biomedical applications, Matter, 2590-2385. https://doi.org/10.1016/j.matt.2021.11.021
Schmitt, J. B. (1938). The feeding mechanism of adult Lepidoptera (4th ed., Vol. 97). Smithsonian Miscellaneous Collections.
Scarr, G. (2019). Biotensegrity: What is the big deal? Journal of Bodywork & Movement Therapies 24(1), 134-137. https://doi.org/10.1016/j.jbmt.2019.09.006
Schulz, A. K., Wu, J. N., Ha, S. Y. S., Kim, G., Slade, S. B., Rivera, S., Reidenberg, J. S., Hu, D. L., (2021). Suction feeding by elephants. The Royal Society. 1742-5662. https://royalsocietypublishing.org/doi/10.1098/rsif.2021.0215#d1e1974
Wilson, J.F., Mahajan, U. Wainwright, S.A., & Croner, L.J. (1991). A continuum model of elephant trunks. Journal of Biomechanical Engineering, 113(1), 79-84. https://doi.org/10.1115/1.2894088
Wilson, T. V. How Butterflies Work. howstuffworks. https://animals.howstuffworks.com/insects/butterfly.htm#pt3
Yang, W., Li, Z.M., Shi, W., Xie, B.H., Yang, M.B (2004). Review on auxetic materials. Journal of Materials Science 39, 3269–3279. https://doi.org/10.1023/B:JMSC.0000026928.93231.e0
Zhang, C., Adler, P. H., Monaenkova, D., Andrukh, T., Pometto, S., Beard, C. E., & Kornev, K. G. (2018). Self-assembly of the butterfly proboscis: The role of capillary forces. Journal of The Royal Society Interface. https://doi.org/10.1098/rsif.2018.0229
Zhang, C.-M., Niu, Y., Hu, G.-L., & Lu, J.-Q. (2021). Ultramorphological comparison of proboscis and associated sensilla of Scotogramma trifolii and Protoschinia scutosa (Lepidoptera: Noctuidae). Insects, 12(11). https://doi.org/10.3390/insects12110992