Resonating Devices in Nature for Communication and Information Reception
Archinlin Wang, Henry Stephenson, Syphax Ramdani, Zachary Flynn
Abstract
Vibrations and resonance are pervasive means of communication and information reception in the animal kingdom. The tools, appendages, and organs used by an animal to amplify vibrations are known as resonating devices, which are the focus of this review. Animals from cicadas to lions employ resonating devices for functions as essential and diverse as perception, courtship, food collection, predator evasion, and social organization. This report will first provide an overview of resonance as a physical phenomenon, then move towards more discrete illustrations in the body section. Each of the four sections analyzes a specific example of a resonating device in animals. This includes a thorough investigation of the manifestation of resonance, the function of the device, and the evolutionary impetus for its creation, all through a physical lens. Biotremological, mechanical, biomaterials, fluids, and architectural engineering perspectives are considered to illustrate the engineering solutions that have evolved through natural selection. In order, this review explores mating calls in cicadas, communicative roars in lions, echolocation in bats, and sensory webs in spiders; it demonstrates the crucial and varied role of resonance in survival and reproduction for many distantly related species of the animal kingdom.
Introduction
Acoustic resonance is the response of a body that vibrates in phase with an externally applied oscillatory vibrational force (Britannica, 2022). It differs from mechanical resonance in that it is specifically in frequency ranges detectable by an organism of interest. In essence, resonance is a phenomenon in which a body amplifies vibrations that oscillate at a resonance frequency of the body. A body has many resonance frequencies; the lowest pitch is called the fundamental frequency, and each integer multiple of the fundamental is known as a harmonic. Through a physical lens, resonance can occur in many situations in nature, but most common manifestations can be approximated by either a string system (like the vocal cords of most animals) or an air column closed at one end (like the air column formed by a lion's throat and mouth). Both approximations will be derived below.
The string system approximation will be explored first. When a string vibrates, locations along the string's axis have different displacements from their resting positions. Locations of maximum displacement (furthest from their resting position) are antinodes, while those with zero displacement are nodes (UCLA, n.d.). Thus, for a string fixed at its ends, there will always be nodes at both ends. Therefore, for resonance (i.e., constructive interference) to occur, the length of the string must be an integer multiple of one half of the wavelength of the vibration, otherwise the vibration will not reflect symmetrically when it reaches one of the fixed ends (See Figure 1 below). The nth integer multiple of half of the wavelength is referred to as the nth harmonic.
Formula 1 conveys the relationship between a fixed wavelength and the necessary length of string for the nth harmonic to form:
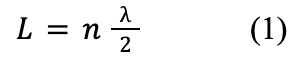
where L is the length of string (in meters, m), n is the harmonic number (n = 1, 2, 3, …), and λ is the wavelength (in meters, m) of the vibration.
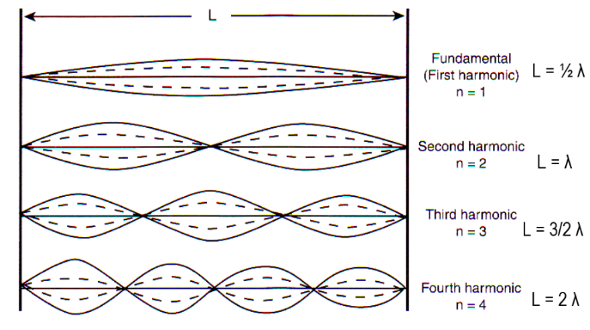
Fig. 1 The fundamental and three lowest harmonics for a string fixed at both ends. [Adapted from UCLA, n.d.].
Formula 2 rearranges the equation above to convey the relationship between a fixed length of string and the necessary wavelength for the nth harmonic to form:

Now, we consider the following relation expressed by Formula 3 (UCLA, n.d.):

where f is the frequency of vibration (in Hertz, Hz), and v is the phase velocity of the vibration (in meters per second, ms-1).
Substituting Formula 2 into Formula 3 and simplifying, we obtain Formula 4, which expresses the equation for calculating the nth harmonic's frequency value in Hz:

Thus, an expression for resonance frequency in string approximations has been established. This formula will be applied to natural resonating devices that can be approximated as string systems throughout this review.
Next, the physical basis for resonance in air columns closed at one end will be analyzed. If one considers a cylindrical shell closed at one end – thus carrying a node at its “fixed” end and an antinode at the open end – an expression for the fundamental frequency can be determined. For a node at one end and an antinode at the other, the fundamental frequency must be the wave with a wavelength equal to four times the length of the cylinder (See Figure 2 below). However, for harmonics, the cylinder length cannot be an even integer multiple of one-fourth the fundamental wavelength, otherwise there will be a node at both ends. Thus, cylinder length can only be odd multiples of one-fourth of the fundamental wavelength (See Figure 2 below).
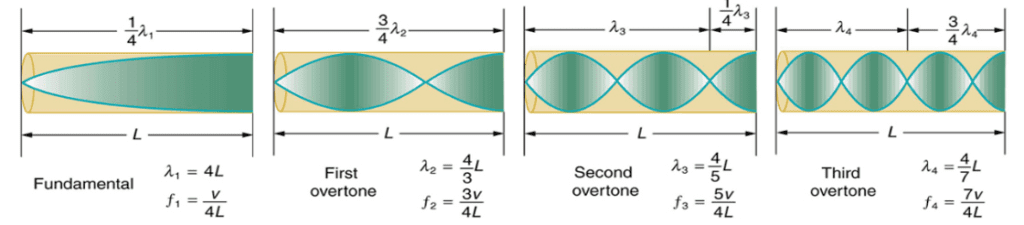
Fig. 2 The fundamental and three lowest harmonics for a tube closed at one end (University of Iowa, n.d.).
Formula 5 conveys the relationship between a fixed wavelength and the necessary cylinder length for the nth harmonic to form:

where L is the length of the cylinder (instead of the string).
Formula 6 rearranges the equation above to convey the relationship between a fixed cylinder length and the necessary wavelength for the nth harmonic to form:

Substituting Formula 3 into Formula 6 and simplifying, we get Formula 7, which expresses the equation for calculating the nth harmonic's frequency value (in Hz):

Thus, an expression for resonance frequency in air column approximations has been established. This formula will be applied to natural resonating devices that can be approximated as air columns throughout this review.
Using these expressions, the following sections will examine the physical manifestations of resonance and other vibrational phenomena in the natural resonating devices of four animals. This review aims to investigate the mating calls of cicadas, the amplification of lion roars for information transfer, echolocation and Helmholtz resonators in bats, and selective vibrational amplification and attenuation in spider webs. Considerations of evolutionary design and several engineering perspectives will be applied throughout to best understand the functions of resonating devices for the fitness of specific organisms.
Resonance in cicada mating songs
Cicadas encompass a variety of species, all of which exhibit unique physical features. However, a common characteristic shared by several species is the ability to sing. Male cicadas sing to attract potential mates in the surrounding environment, acting like a beacon for female cicadas. Male cicadas accomplish this through resonating devices found within their body, which create reverberating, high amplitude songs despite the cicada's humble stature. While cicada songs vary greatly between species, and even between different subgroups, their singing mechanisms are relatively similar (Young & Bennet-Clark, 1995). Usually, the mechanism consists of a tandem system of two resonating devices: the tymbal and the tympanas. To understand how these resonating devices work together, we must first dissect the mechanics behind the muscle groups which power the tymbal (the main resonating device). This will also require an explanation of the biochemistry between these muscle groups, which is crucial to understand the mechanical notions behind each muscle group. Finally, the resonating devices employed by cicadas will be discussed to demonstrate how evolution has designed these devices according to common principles in physics.
Mechanical functions of the muscle group behind the tymbal
Cicadas have one primary muscle group in their abdomen that enables them to sing. This muscle group consists of three muscles: the tymbal muscle pair, the tensor muscle, and the ventral longitudinal muscle (Stokes & Josephson, 2004; Young & Bennet-Clark, 1995). The tymbal and tensor muscles interact directly with the tymbal. The tymbal generally consists of a planar-circular membrane which is reinforced yet flexible (Stokes & Josephson, 2004). The ventral longitudinal muscle depresses or expands the abdomen which changes the size of the opening between the abdomen and the metathorax. This helps modulate the volume of the cicada's song because this is where the sound waves radiate out of the cicada (Stokes & Josephson, 2004). The tensor muscle is fan-shaped and directly attached to the tymbal from the edge of the metathorax (Stokes & Josephson, 2004). Its motion controls the rigidity of the tymbal itself, which modulates the amplitude of the resulting sound waves (Stokes & Josephson, 2004). The tymbal muscle is directly attached at the base of the tymbal, as seen in Figure 3.
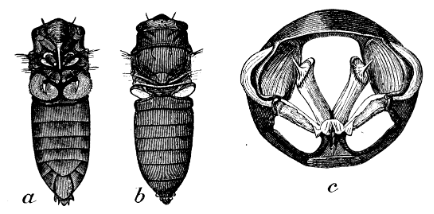
Fig. 3 a. and b. show the general anatomy of the cicada. c. demonstrates the tymbal muscles (long cylindrical structures in the center) and the tensor muscles (attached to the bottom). The tymbal are the etched structure on the sides (Hemiptera, 2011).
Its contractions exert a force on the tymbal creating a 1st class lever; levers are simple machines that utilize torque to obtain a mechanical advantage. They consist of a force which provides the torque, a rotation point (fulcrum) and a resultant force in the direction of rotation (load). There are three classes of levers, each with different placements for its three components, as each placement has unique characteristics. In this case, the force is the contraction of the muscle, the fulcrum is the base of the tymbal, and the load is the tymbal itself. One advantage of a 1st class lever is that the load travels much further than the exerted force, which stands true in the tymbal's case; the tymbal moves twice the distance of the muscles' contracting motion (Young & Bennet-Clark, 1994). The tymbal muscles are the largest muscles within the group; they are bigger than both the tensor and ventral longitudinal muscles by approximately one order of magnitude (Stokes & Josephson, 2004). It is important to note that muscle power is proportional to mass and size, which indicates that the tymbal muscles are power muscles and the tensor and ventral muscles are small control muscles. This point is further demonstrated by the biochemical characteristics found within these muscles.
Biochemical nature of the muscle group
Power muscles, such as the tymbal muscles, are richly supplied by mitochondria, while control muscles lack significant power production (Stokes & Jefferson, 2004). This is because power muscles require a high and sustained rate of ATP to exert the forces that their functionality requires. This is especially true for the tymbal muscles, which must contract and relax at a relatively high frequency (Stokes & Josephson, 2004). Control muscles, such as the ventral longitudinal muscle, do not have to emit such large amounts of mechanical power and thus lack the same concentration of mitochondria. Furthermore, the innervation of each muscle within the group differs substantially based on its function. A muscle's innervation is provided by motor axons; electrical signals within the peripheral nervous system are converted by these neurons into physical impulses within the muscle. The neurotransmitter acetylcholine released from the synapses of the motor axons and binds to receptors within the muscle fibers, causing an action potential to occur (Knierim, n.d.). An action potential is a rapid change in a cell membrane's voltage caused by a transfer of ions with its surroundings, creating an electrical signal which causes contraction in muscles. A motor unit consists of a motor axon and all the muscle fibers it innervates (Knierim, n.d.). The number of motor units as well as their size indicate the function of the muscle group they direct. For example, the tymbal muscles are each innervated by a single but relatively large motor unit, which has a short and binary twitch. The tymbal muscles have minimal complexity within their motion; they are either entirely contracted or relaxed. This is appropriate given that power muscles need short twitches to exert a large force due to Newton's first law, and they also have anti-fatigue characteristics useful for high frequency operations (Knierim, n.d.). The ventral longitudinal muscle has a highly complex motion and thus has more than six motor units (Stokes and Josephson, 2004). Additionally, the ventral muscle's innervation is slow, which reflects how control muscles exert forces over longer increments of time, using less power (Stokes and Josephson, 2004).
The tymbal as a resonating device
Now that we understand the muscles controlling the tymbal, we can analyze its resonating motion to delineate how cicadas sing. As established, the tymbal buckles in due to the torque exerted by the tymbal muscles, deforming towards a set of consecutive, parallel ribs (Young & Bennet-Clark, 1994). These ribs are embedded in resilin meaning that they are fixed at both ends (Young & Bennet-Clark, 1994). As demonstrated in Figures 4 and 5, the tymbal translates backwards, pushing into the first rib; however, since the rib is fixed on both ends, it deforms at its weakest point.
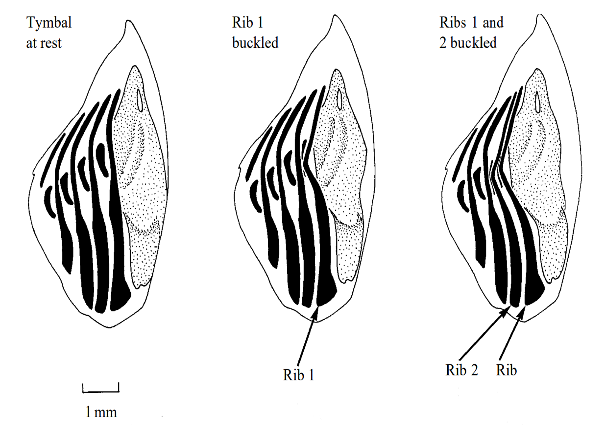
Fig. 4 Cycle of the tymbal resonator. As the tymbal translates backwards, it causes the parallel set of ribs to deflect (Stokes & Josephson, 1994).
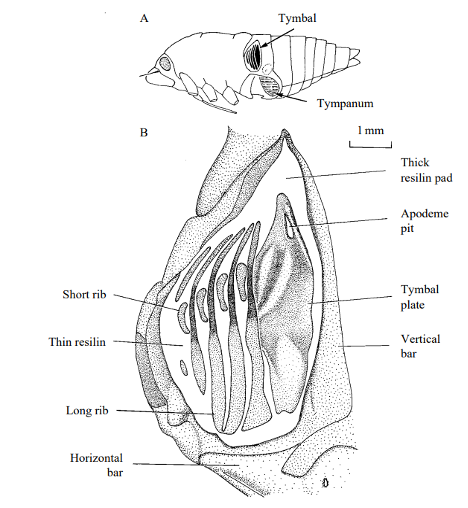
Fig. 5 Closeup of the tymbal resonator and ribs (Stokes & Josephson, 1994).
The rib deflects because the force exerted by the tymbal is greater than the restoring force provided by the elasticity of the rib (Stokes & Josephson, 1994). The tymbal continues to move backwards towards the other ribs, causing up to three ribs to deflect, much like an elastic band (Stokes & Josephson, 1994). As the tymbal muscles relax, and the tymbal moves back to its initial position, the ribs rapidly regain their original, non-deflected shape. The elastic energy stored within the rib is quickly released into kinetic and sound energy, producing an audible click (Stokes & Josephson, 1994). As the tymbal oscillates rapidly, the ribs undergo several deformations per second, and the rapid series of consecutive clicks produces the cicada's song. The dominant frequency emitted from these ribs depends on the position of the tymbal. The largest ribs produce sound waves at a frequency of around 4 kHz, while the smaller ribs oscillate closer to 6 kHz (Stokes & Josephson, 1994). These waves are amplified by the tymbal itself; its frequency will match the waves produced by the ribs, and the exiting sound waves are amplified much like a tuning fork (Stokes & Josephson, 1994).
Helmholtz resonance used to amplify the cicada song
In certain cicada species, such as Tympanistalna gastrica, the tymbal resonator is the only sound-producing system (Michelsen & Fonseca, 1999). In other words, these cicada species have evolved only one resonating system to sing. However, some other species, such as Cyclochila australasiae utilize tandem resonators to create mating calls (Young & Bennet-Clark, 1994). The first is the tymbal resonator described in the previous paragraph. The second consists of a structure which acts as a Helmholtz resonator. This structure consists of a pair of tympanas, large but thin membranes containing an air sac which takes up substantial volume within the abdomen of the cicada (Young & Bennet-Clark, 1994). To understand how these air sacs function, we must first grasp how Helmholtz resonators amplify sound waves.
A Helmholtz resonator is a container filled with gas, usually air, which has nondescript dimensions. It has a long, linear opening of a relatively small surface area compared to the volume found within the air chamber (Berg, 2022; Wolfe, 2005). As sound waves enter the resonator, the air within the neck compresses and is displaced towards the main chamber. Eventually, the air ceases to compress because the restoring force provided by the air pressure inside the chamber is greater than the compression provided by the sound waves entering the resonator. The air decompresses in the opposite direction, creating a cycle of compressions and decompressions analogous to a mass on a spring (Wolfe, 2005). Thus, like a mass-spring system, gasses have elastic properties; they can be compressed and decompressed adiabatically (see Figure 6).
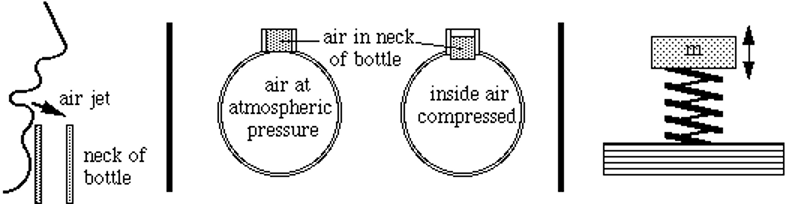
Fig. 6 Analogy between Helmholtz resonator and a spring-mass system. The compressed air within the neck of the resonator resembles the oscillating motion of a mass on a spring, which amplifies incoming sound waves of specific frequencies (Wolfe, 2005).
Usually, the sound waves entering the resonator have several distinct frequencies. Frequencies which match the oscillation of the air current get amplified, given that their waves are in phase. The sound waves which are out of phase with the oscillating air-mass enter the air chamber and reflect off the opposite end. This creates a standing wave within the resonator, where the reflecting waves are out of phase and destructively interfere with the incoming waves (Berg, 2022). Mechanically speaking, a Helmholtz resonator is useful in amplifying a very specific frequency and attenuating surrounding frequencies (Berg, 2022). The amplified frequency, f, is given by Formula 8 below:

where v is the speed of sound in the volume, A is the area of the opening, L is the length of the opening, and V is the volume of the resonator (Berg, 2022).
Within the species Cyclochila australasiae, a combination of 4 kHz and 6 kHz enters the air sac within the tympanas. The 4 kHz waves are amplified, while the 6 kHz waves are mostly attenuated by the geometry of the resonator (Stokes and Jefferson, 1994). This tandem system of resonators is what allows the cicada to produce such loud noises. This is incredibly important in the cicada's reproductive success. Given that sound waves follow the inverse square law, where the intensity of a signal is inversely proportional to the distance squared, it is important for cicadas to produce loud sounds to alert potential mates for reproduction. In other words, having compact but effective resonators within its body allows a cicada's mating call to be heard from longer distances, attracting a greater selection of mates. The beauty behind evolution is its ability to use common themes in chemistry and physics, such as Helmholtz resonators, circuitry like that in motor neurons, or even elasticity within a cicada's ribs, to create beautifully complex biological structures that contribute to an organism's biological fitness.
Communicative functions of resonance in lion vocalizations
The roar of Panthera Leo, or the lion, is another example of resonance in nature. Lions communicate with conspecifics predominantly through vocalization. Their primary habitats are savannahs or semi-deserts where the terrain is open and flat, facilitating air-borne acoustic information transfer. Adult male lions are observed to roar at average volumes of 114 decibels, though their calls have been measured to be of substantially higher amplitude than the figure provided; some reports say they can be heard up to five miles away (Titze, 2012). Their growls serve as a warning to attackers and as a symbol of power within their domain.
This section has three primary foci. First, the waveform produced by lion roaring is examined in detail. Then, a mechanical analysis of the lion's vocal folds is conducted to determine how lions physically produce their vocalizations. Finally, we investigate the social function of resonance in a lion's roar for communication.
First, we provide a brief introduction to airborne vibration to better understand the waveform produced through the Panthera leo roar. At the most fundamental level, the movement of individual particles between regions of low and high particle density is what causes airborne sound. A vibrating molecule moves fast back and forth in an oscillating pattern. It collides with the adjacent molecule, which consequently also vibrates. The vibrations form a wave pattern as the sound propagates from its origin. There are two properties of waves: amplitude and frequency. As described in the Introduction section, a wave's amplitude correlates with the volume of a sound wave. It equally corresponds to how much vibrational energy a wave carries; higher energy waves cause greater displacement of individual particles from resting position. The other concept, frequency, is the number of oscillations a wave undergoes per unit time. In other words, if individual air particles oscillate quickly between a resting position and a non-resting displacement, they will have a high frequency, while low-pitched sounds oscillate slowly.
In 1976, Smith and Tsurutani discovered that lion roars are narrow-banded, right-handed polarized waves with a typical frequency of around 120 Hz and a typical amplitude creating a magnetic field equivalent to 0.1 nanoteslas (nT) in a computer measurement. These waves have a very short lifetime of about 2 seconds and are essentially electron cyclotron waves (Smith & Tsurutani, 1976). The lower panel of Figure 7 shows the spectrograms of the right-hand polarized signals. The left-most diagrams show one of the strongest and longest lion roar signal waveforms found in the data set, about 10 wave cycles with an amplitude equivalent to 1 nT. The signal is nearly a single tone with a center frequency near 15 Hz. The lion roar in the middle panels has a frequency of 21.5 Hz, which is a bit higher than the background frequency. Moreover, it is evidently broken into 3 to 4 wave packets, some of them lasting only for 2 to 3 wave cycles. The third lion roar (in the right-most diagrams) has a somewhat different center frequency (about 18 Hz). A clear packet structure can also be seen in Figure 8, which shows waveforms and wavelet spectrograms for two other lion roar wave packets inside a magnetic trough (Baumjohann et al., 1999).
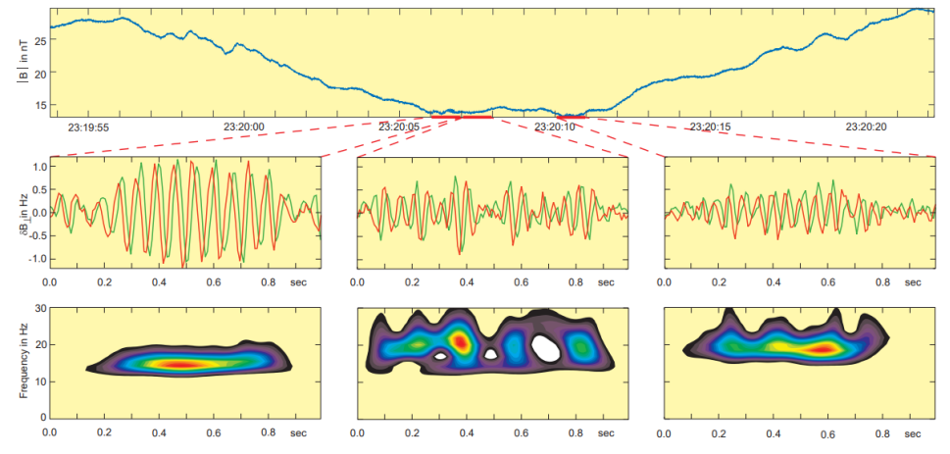
Fig. 7 Mirror mode trough, embedded lion roar wave forms perpendicular to the mean field, and right-hand polarized wavelet spectrogram (Baumjohann et al., 1999).
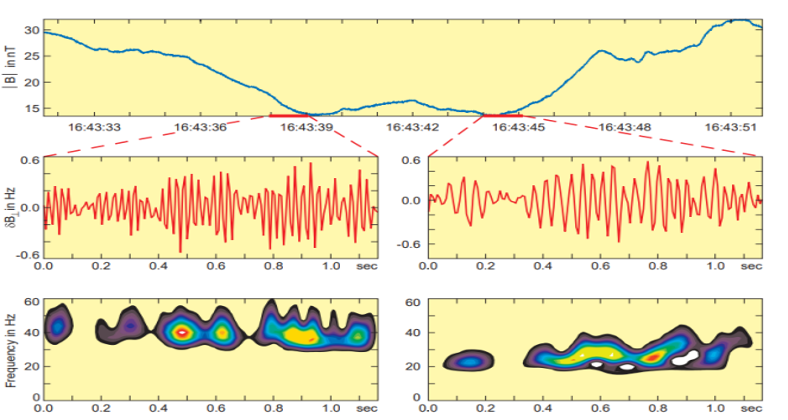
Fig. 8 Mirror mode trough, another embedded lion roar wave forms perpendicular to the mean field, and right-hand polarized wavelet spectrogram (Baumjohann et al., 1999).
The instrument that detects roaring – the Equator-S magnetometer – has an average sample rate of 128 Hz (i.e., 128 samples per second) and is exceptionally sensitive for testing and recording lion roars. Fornacon et al.'s description of the Equator-S magnetic field sensor is comprehensive; it is made up of two components, each housing two three-axis fluxgate magnetometers. The main sensor is at the end of a 1.8-m boom, while the other is 50 cm farther inboard. Both the primary and redundancy units' sensors are positioned on two sturdy booms (Fornacon et al., 1999).
One can analyze the anatomy of the lion's vocal folds and larynx structure to determine why the lion is able to produce such a high amplitude, low-frequency roar. Vocal cords consist of two membranes that vibrate to produce sound when the muscles of the voice box bring them close together. In most vocal species (apart from birds, which have no vocal cords), the two membranes are slightly curved (University of Utah, 2011). However, in species of the Panthera genus, an uncommon layer of fat shapes the cords into flat pads that vibrate more easily. Recent research shows that lions, along with tigers, have unusual vocal cords that are fine-tuned for making loud and raspy noises even without significant respiratory exertion. Species of the Panthera genus have vocal folds that are around three times as long as those of humans, measuring between 2.5 and 3.5 cm; the frontal cross-section of a lion's vocal cords is shown in Figure 9 (Titze, 2012).
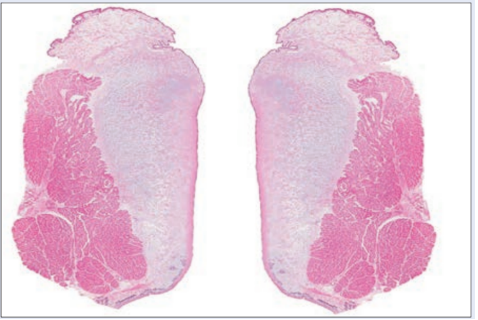
Fig. 9 Pair of lion vocal folds (Titze, 2012).
Lengthy vocal folds are known to generate low-pitched sounds akin to long piano strings. The epihyal bone seen in most mammals had been replaced by an elastic ligament that was 6 inches long when Owen discovered the lion's incomplete ossification of the hyoid apparatus in 1834 (Hast, 1989). According to Owen, this ligament could be stretched to 8 or 9 inches, allowing the lion to move its larynx further from the palate and gradually lengthen the pharyngeal passage. The lion's roar derives much of its power from the square shape of its vocal folds (see Figure 9 to the right) (University of Utah, 2011). This form stabilizes the vocal cords, allowing them to respond more effectively to airflow. Thus, lions can make loud roars without excessively straining their lungs.
Now that we have seen the waveform of a lion's roar and how lions produce airborne vibrations through their vocal cords, we will discuss the communicative function of resonance in lion vocalization. Roars are used to communicate territory and to find members of a pride that are far away. Both male and female lions indicate territory ownership by roaring, and they may determine the degree of resistance depending on the number of roars they hear from rival groups. Several researchers have utilized playback tests to evaluate the response of lions to the replay of roars from a varying number of pre-recorded lions (Scheel & Packer, 1991). Females are more likely to respond to the roars of rival groups only when they outnumber their rival pride, but males counter the roars of competing lions regardless of their numbers. Fights between females frequently end in serious injury or death; hence it is essential for lionesses to assess the dangers before engaging (Sranko, 2022). Fights between males are usually fatal as well, but males in a pride can only succeed at reproducing when they rule a pride; thus, they are much more likely to initiate and respond to roars (Grinnell & McComb, 2001).
Another interesting peculiarity is that lions tend to roar exclusively at night. A recent study discovered that lions roar more frequently when acoustic circumstances are favorable to sound propagation across long distances (Lindsey, 2021). Lions roar more frequently when wind speed and temperature are low and the relative humidity is high (Lindsey, 2021). They refrain from roaring beyond the boundaries of their native range and are more likely to vocalize near rivers and water sources (Denise Cassano, 2020). These incredible discoveries advance our understanding of the intricate social structures in lions.
In conclusion, lions have a unique square shape to their vocal cords, with flat pads made of a fat layer that allows their roars to travel further. In addition, lions use favourable environmental factors, such as low temperatures and high humidity at night to enhance their roars and fend off enemies at a distance, all while maintaining the integrity of their pride.
Echolocation in bats: resonance analysis of the larynx and pinnae
Most bats have evolved an active biosonar, or echolocation, as a tool to sense their environment in low-light conditions (Metzner & Müller, 2016). In echolocation, the bat emits a sound and listens for its echo, from which it can glean comprehensive information about its environment. A target's relative position can be determined by the time delay between the emission and reception of the sound, the difference in volume between the left and right ear, and reflections caused by the bat's external ear. A target's size can be accurately estimated from the volume of the echo, its texture from interference patterns in the echo, and its speed from a difference in the frequency of the echo due to the Doppler effect (Metzner & Müller, 2016; Jones, 2005; Jones & Holderied, 2007). To rely on echolocation, bats have evolved a vocal tract capable of producing frequent and diverse high-intensity sounds, as well as external ears able to magnify and modify returning sounds.
Bats emit a wide variety of echolocation calls, adapting the call type, frequency, duration, and amplitude to adjust to different situations. An insectivorous bat's call frequency usually lies in the 20 to 60 kHz range and its intensity extends from 80 dB to over 120 dB (Jones, 2005). These high intensity ultrasonic signals are essential for accurate echolocation. High frequency leads to higher resolution echolocation, as a wavelength greater than the insect's wingspan results in a weak echo. Higher intensities are preferred to increase the range at which the bat can detect the reflected sound. Bats can emit both short frequency-modulated (FM) sweeps and longer constant-frequency (CF) calls. CF calls are better for long-range detection and motion determination. They travel farther, and Doppler shifts are easier to detect when only one frequency is present. FM sweeps consist of shorter calls with a sharply increasing or decreasing frequency. They provide the bat with an accurate, fast-updating estimate of a target's distance away; the frequency of the call and echo change for each vocalization, so several calls can be vocalized at once without complicating echo detection. Bats can also analyze the diffraction pattern from multiple frequencies to glean information on prey shape and texture. They can use either CF or FM components separately in an echolocation call or combine them in a variety of arrangements depending on species and circumstances (Jones, 2005; Simmons, 1973; Simmons & Stein, 1980).
Laryngeal sound production
Bats produce sounds from the larynx which travel up to be emitted through the mouth or nose. A simplified sketch of the larynx of a horseshoe bat is shown in Figure 10. The larynx lies above the trachea and contains three important pieces of cartilage: the thyroid cartilage (or “Adam's apple”), the cricoid cartilage, and the arytenoid cartilage. The vocal folds extend from the thyroid cartilage to the arytenoid, and the space between the vocal folds is called the glottis. Multiple muscles connect the different cartilages, including many which are not shown in Figure 10. Most importantly, the cricothyroid muscle, stretching between the cricoid and the thyroid cartilages, is a fast-twitching muscle which controls the stretching of the vocal folds. The air chambers appear only in some species of bats (Metzner & Müller, 2016).
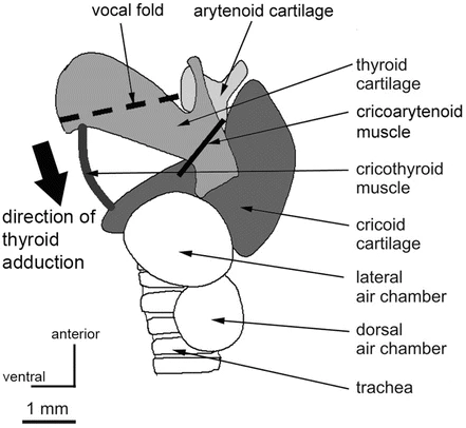
Fig. 10 Side view of a schematized horseshoe bat larynx. The arrow indicates the visor-like adduction of the thyroid cartilage through the action of the cricothyroid muscle (Metzner & Müller, 2016).
Phonation in bats happens in much the same way as in most other mammals (Suthers & Fattu, 1973). The leading theory for sound production in the vocal folds of mammals is the myoelastic-aerodynamic (MEAD) theory of phonation, which explains how vocal folds vibrate to create air pressure waves. Phonation occurs when the vocal folds are brought together to close the glottis at the same time as pressure increases in the lungs from expiration. After a moment, enough pressure develops underneath the vocal folds to force them apart, allowing for a brief burst of air to pass through. Afterwards, the combined action of the elastic force of the vocal folds and the force generated by the change in pressure caused by the Bernoulli effect (discussed below) forces the vocal folds shut once more. Pressure builds again, and the cycle repeats, creating the oscillating motion necessary to create sound waves (Herbst, 2016).
An understanding of Bernoulli's principle is essential to grasp the MEAD theory. Bernoulli's equation can be written as shown in Formula 9 below:
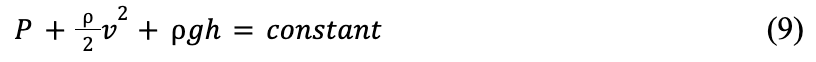
where P is the static pressure, ρ is the fluid density, V is the fluid velocity, g is the gravitational acceleration and h is elevation.
Bernoulli's equation states that the sum of the static pressure (P), dynamic pressure (½ ρV 2), and hydrostatic pressure (ρgh) of a fluid must remain constant. Figure 11 shows a model of air flow in a bat's vocal folds, with position 1 under the glottis, and position 2 inside of the glottis.
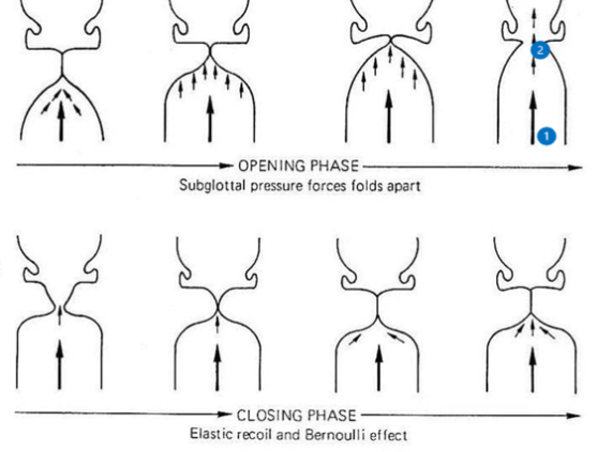
Fig. 11 Different steps in the opening and closing of the glottis in the MEAD theory of phonation. Subglottal (1) and glottal (2) positions are labelled [Adapted from Laver, 1993].
Since the change in height between the points is small compared to the corresponding change in velocity, hydrostatic pressure can be ignored, leading to Formula 10:
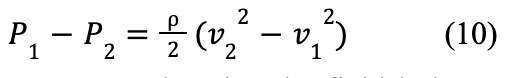
Assuming that the fluid is incompressible, for mass to remain constant, the mass of air crossing through the trachea per unit time must
equal that of the glottis. This leads to the equation given by Formula 11:

where A is the cross-sectional area.
This equation demonstrates that as air passes through the much tighter glottis, its speed greatly increases. As the air's speed increases, Formula 10 shows that its static pressure must decrease (The Efficient Engineer, 2020). It is this negative pressure, in addition to the elasticity of the vocal folds, that forces the glottis to close during phonation.
In bats, the vocal folds are closed through the action of the cricothyroid muscle, which contracts to adduct the thyroid cartilage towards the cricoid cartilage in a visor-like fashion (Metzner & Müller, 2016). The fundamental frequency of the vocal folds determines the fundamental frequency of the call. Though it is an approximation, the vocal folds can be modeled as strings, leading to the following equation for fundamental frequency (Formula 12):

Where f0 is the fundamental frequency, L is the length, σ is the tensile stress, and ρ is the tissue density (Herbst, 2016).
Thus, bats increase the fundamental frequency of their vocal folds by exerting tension on them through the action of the cricothyroid muscle. Other laryngeal muscles can open and close the glottis independently from the action of the cricothyroid muscle, which can block air flow completely. By blocking air flow at different levels of contraction of the cricothyroid muscle, bats can produce multiple combinations of FM and CF calls as shown in Figure 12 (Metzner & Müller, 2016; Suthers & Fattu, 1973).
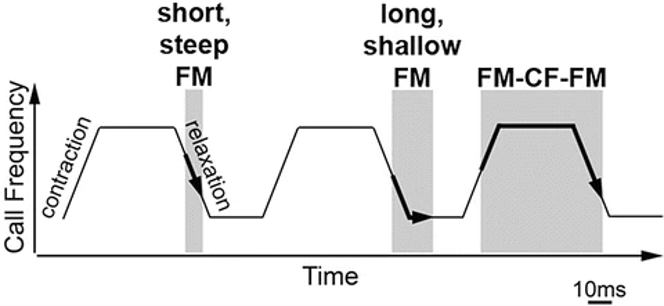
Fig. 12 Model of sound production by the larynx. Grey regions indicate an open glottis. By independently opening the glottis and stretching the vocal folds, bats can create many different types of calls (Metzner & Müller, 2016).
To achieve high-intensity, high-frequency calls, bats have evolved several adaptations. To withstand high tensions and pressures, their vocal folds are thicker and the cartilage in the larynx exhibits a high degree of calcification or ossification compared to other mammals. The cricothyroid muscle is hypertrophied and unusually fast-twitching to allow for rapid change in frequency and for the production of multiple calls in a short time. Moreover, the arrangement of abdominal muscles in bats is unique among animals. Their flank muscles do not create movement of bones, but push air out of the lungs. Bats use this to create the pressure needed for loud echolocation calls (Metzner & Müller, 2016).
Sound modification in the vocal tract
After sound is produced in the larynx, it must travel up the vocal tract, the shape of which can change the features of the sound. An example of this is the air pouches of horseshoe bats (Rhinolophus hildebrandti), shown in Figures 10 and 13. Horseshoe bats emit calls through their nose and have air pouches under the glottis (labelled lt and dd in Figure 13) and in the nasal cavity (labelled dn, ln, and pn in Figure 13). These features function as Helmholtz resonators (discussed in further detail in the section on cicadas), which are highly effective at attenuating all frequencies except the fundamental frequency of their calls. These pouches may then reflect the fundamental frequency, phase shifted by 180°, to cause destructive interference. The reason for this is unclear, though it is hypothesized that this prevents the transmission of sound waves through the bat's tissues and directly to the cochlea (Suthers et al., 1988).
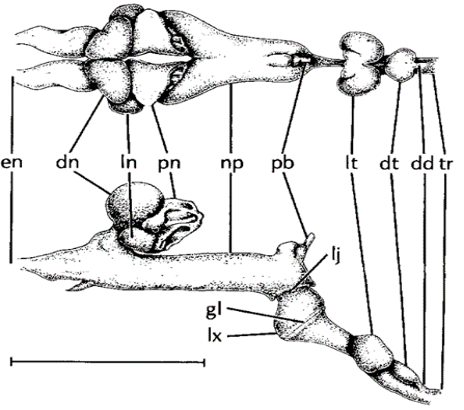
Fig. 13 Dorsal and lateral views of the vocal tract of R. hildebrandti: en external nares; dn dorsal nasal chamber; ln lateral nasal chamber; pn posterior nasal chamber; np naso-pharynx; pb duct of pharyngeal bursa; lj laryngonasal junction; gl glottis; lx larynx; lt lateral tracheal chamber; dt dorsal tracheal chamber; dd duct connecting dorsal tracheal pouch to trachea; tr trachea. Scale is about 1 cm (Suthers et al., 1988).
External ear features
The echolocation process relies both on the production and reception of sound. The external ears, or pinnae, of bats have evolved several features to increase the amount of information that they can receive and process. Two such features are the ridges on the inner side of the pinna and the prominent tragus shown in Figure 14. The ridges function as both an acoustic version of a Fresnel lens (See Figure 15) and as a diffraction grating. Fresnel lenses are commonly used in lighthouses as they possess the same focal length as a lens of equal area, but are much lighter and use less material (Britannica, 2011). Bats use these ridges to focus the sounds into the ear canal while keeping a light, aerodynamic shape. The ridges also act as a diffraction grating for sounds of wavelength comparable to the separation between grooves. Since the ridge separation averages at 1 to 2 mm, the diffraction grating is only effective for frequencies of at least 150 to 180 kHz, with peak performance when the frequency is over 300 kHz.
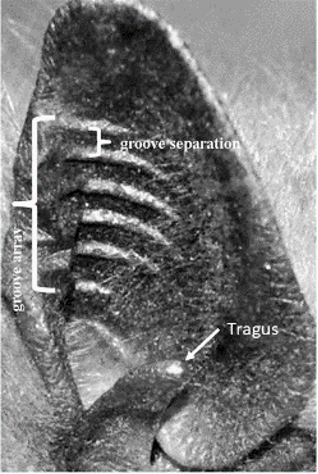
Fig. 14 Pinna of a big brown bat (Eptesicus fuscus). The ridges (grooves) and tragus are indicated [Adapted from Keeley et al., 2018].
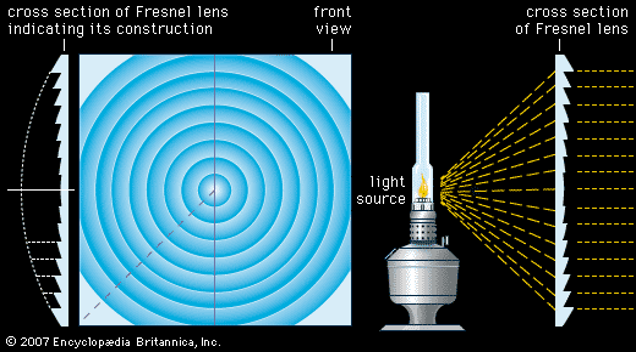
Fig. 15 Frontal and cross-sectional views of a Fresnel lens. The cross-sectional view on the left shows that the Fresnel lens uses less material than an equivalent convex lens. However, Fresnel lenses still have a short focal length (Britannica, 2011).
A diffraction grating can intensify sounds according to Formula 13:

where I0 is incident intensity, n is the number of ridges, and I is the reflected intensity.
Therefore, these ridges may also intensify high-frequency sounds. These high-frequency sounds may correspond to the third or fourth harmonics of their calls, which provide higher resolution. They may also correspond to sounds that their prey produce (Keeley et al., 2018; Kuc, 2009).
One problem that the ridges pose is that they are only approximate Fresnel lenses. Indeed, the lower ridges can block sound from the higher ridges, reducing their performance. The tragus solves this problem by reflecting soundwaves, increasing the ridge area that receives sound (as illustrated in Figure 16) (Kuc, 2009). In addition, the tragus serves to determine the relative altitude of a subject, demonstrating another example of multifunctionality in nature. Pinna-tragus interactions cause a reflection of the incident sound, which can be detected by the ear a few microseconds after the original sound is received. The duration between detection of the initial sound and this reflection varies depending on the relative height of the source. Thus, this delay may be used by bats to detect the relative height of targets (Lawrence & Simmons, 1982).
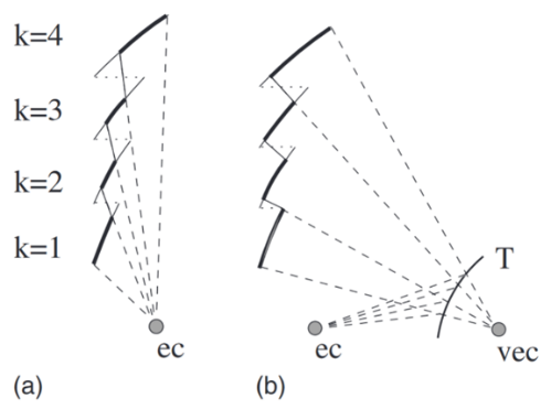
Fig. 16 Cross section of model ridge structure. Light lines correspond to the ridges, while dotted lines correspond to the horizontal connection between ridges for an ideal Fresnel lens. Bold lines show the area that can properly reflect sound to the ear canal. ec corresponds to the ear canal, vec to a virtual ear canal, and T to the tragus. (a) represents direct reflection to the ec, while (b) represents secondary reflection by the tragus. A greater reflection area on the ridges is present in (b) (Kuc, 2008).
Summary
This section has analyzed some of the structures and mechanisms involved in sound production and reception in echolocating bats. Laryngeal sound production was first examined; The MEAD theory of phonation explains how the elasticity of the vocal folds and the laryngeal changes in pressure create vibrations of the vocal folds. To create a variety of loud, high-frequency calls, the larynx has evolved specialized muscles and a more robust larynx, among other things. Then, air pouches, which act as Helmholtz resonators, were taken as an example of vocal tract structures which modulate the emitted sound. Finally, the ridges and tragus in bat pinnae were analyzed. The ridges focus sound by acting as a Fresnel lens, intensifying high-frequency sounds through diffraction. The tragus creates a more efficient Fresnel lens structure and allows for the determination of a target's relative height.
The spider web: the spider's vibrational sensory system
The spider web is an ancient example of multifunctional resonance in natural design. Modern webs serve primarily to capture prey and provide a substrate for vibrations to travel from prey to spider (Masters, 1984). They act as an extension of the animal's body (Mortimer et al., 2018), enabling spiders to accurately distinguish between prey-produced vibrations, conspecific vibrations (often used in courtship (Frohlich & Buskirk, 1982)), vibrational indicators of avian predators (Klärner & Barth, 1982; Lohrey et al., 2009; Stafstrom et al., 2020), and environmental noise from rain or wind (Masters, 1984); spiders selectively tune their webs to localize vibration sources (Mortimer, 2017), filter out biologically irrelevant information (Mortimer et al., 2016), and amplify (via resonance) a limited range of important frequencies (Frohlich & Buskirk, 1982; Mortimer, 2019; Mortimer et al. 2013, p. 43; Mortimer et al., 2016). Web tuning is achieved through control of web tension, geometry, and silk modulus (Mortimer, 2017). This section will examine the physical design of the spider web as a resonating device using biotremological, mechanical, biomaterials, and architectural engineering perspectives.
Evolutionary impetus for resonance in spiders
While many of today's 47 000 species in the Araneae order construct webs to ensnare prey ranging from midges to small birds (Sensenig, Agnarsson, & Blackledge, 2010), the most ancient spiders lacked spinnerets – the appendages that allow spiders to spin silk (Mariano-Martins, Hung, & Torres, 2020) – likely because spiders used to be free-roaming hunters (Vollrath & Selden, 2007). Some modern species, like their ancient ancestors, are hunting spiders – species whose primary method of predation is not web-building – such as wolf spiders (Lycosidae) and jumping spiders (Salticidae) (Morehouse et al., 2017). Hunting spiders tend to be diurnal and thus rely heavily on visual sensory modes to track and capture prey (Morehouse et al., 2017). Given the success of hunting spiders, the existence of web weavers – who are nocturnal and have more rudimentary visual systems (Morehouse et al., 2017) – might seem peculiar. Why would spiders abandon visual acuity for nocturnal activity?
The answer lies in the origins of silk as a vibrational information transmitter. The first use of silk for predation was likely to create terrestrial signal lines to detect nearby prey (Kaston, 1964; Vollrath & Selden, 2007). By the Late Carboniferous period, circa 325 million years ago (Ma), the first winged insects emerged (Ross, 2017). This evolutionary radiation created selective pressure for spiders to develop strategies to exploit aerial insects. One development was spinnerets, which emerged around 305 Ma (Garwood et al., 2016; Mariano-Martins, Hung, & Torres, 2020), enabling spiders to create intricate, raised (above ground level) web traps (Vollrath & Selden, 2007). Given that insects are less likely to see (and evade) traps in lower light settings, web weavers adjusted to nocturnality. However, instead of evolving energy-expensive nocturnal visual systems, web weavers multi-functionalized their webs to be capable of both capturing prey and notifying the spider through vibrations of trapped prey (Masters, 1984), effectively making the web the spider's main sensory mode.
Hence, modern web weavers have highly sophisticated vibrational systems to extend their sensory space, which compensates for their simpler visual systems (Landolfa & Barth, 1996; Naftilan, 1999). Through a biotremology lens, resonance originally developed as a means of notifying web-weavers of ensnared insects through the amplification of their struggling vibrations (Frohlich & Buskirk, 1982; Mortimer et al., 2016; Naftilan, 1999). However, the functions of vibration and resonance in the web have expanded to include courtship rituals, avian predator evasion, and frequency filtering (Klärner & Barth, 1982; Walcott & van der Kloot, 1959). The following subsections will first review the physical basis for resonance, explore the mechanical intricacies of spider webs, and examine the functions of resonance for web-weaver fitness.
Physical basis for adaptable resonance in the web
Resonance materializes in two distinct ways in spider webs: from vibrations of equal frequency to the resonance frequency of silk threads, and those equal to the natural frequency of the spider (or other bodies). The former is manipulatable by the spider, while the latter is an immutable property; the spider cannot alter the natural frequency at which it resonates. Hence, silk resonance will be the concentration of this subsection.
Determining resonance frequencies for silk threads first requires a mechanical understanding of standing wave formation on strings. The Introduction section has already developed the physical basis for string approximations. When a string vibrates, individual particles along the string's axis have displacements from their resting positions. If displacement is along the axis of the string, this is longitudinal vibration, while if it is perpendicular, this is called transverse vibration (Frohlich & Buskirk, 1982). Figure 17 below demonstrates the difference.
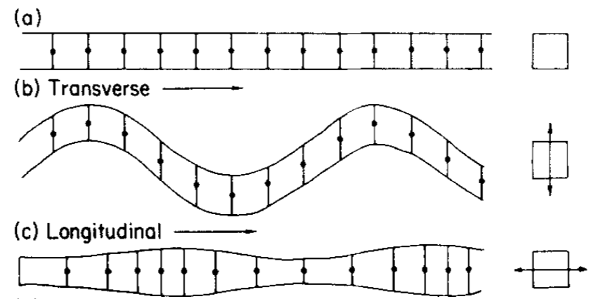
Fig. 17 (a) A string at rest. (b) A string in transverse vibration. (c) A string in longitudinal vibration (Frohlich & Buskirk, 1982).
Formula 4 from the Introduction section has defined an equation for the nth harmonic's frequency which relies solely on a vibration's phase velocity and the length of the string. Now, Formula 14 considers how phase velocity is determined by the physical properties of the web (Frohlich & Buskirk, 1982):
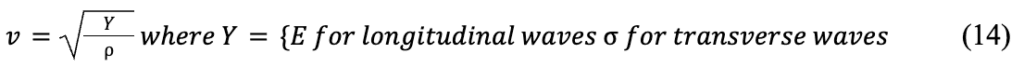
where Y is a placeholder, E is Young's modulus, σ is stress, and ρ is density.
If Formula 14 is substituted into Formula 4, we get Formula 15:

It should be noted that Formula 15 is a theoretical equation that does not account for inevitable attenuation (damping) in the threads (Frohlich & Buskirk, 1982). However, attenuation only slightly alters calculated frequencies and in fact broadens the frequency range that causes resonance (Naftilan, 1999). Thus, the resonance frequencies of silk strings in a spider web are essentially solely determined by the silk's mechanical properties, such as thread length, density, and either the stress or Young's modulus, depending on the wave type (Mortimer et al., 2016). Many Araneae species, especially orb weaving spiders, are incredible biomaterial engineers; they can independently modify any of these properties in their silk threads, manually controlling the resonance frequencies of their webs (Römer & Scheibel, 2008; Su et al., 2018). They do this using biomaterials, mechanical, and architectural principles.
The primary biomaterial manipulation consists of changing proline concentration in specific silk types; proline disfavours the formation of ordered secondary protein structures, like α-helices and β-sheets, disrupting crystalline structure in spider silk (Liu et al., 2008). Hence, proline-heavy silk is more elastic due to greater structural disorder (Liu et al., 2008). Spiders also make use of two post-processing mechanical controls to manipulate the physical properties of the web: active tensioning – where spiders increase tension in radial threads by pulling them – and super-contraction – a process whereby slack silk fibers contract up to 50% when exposed to water (Mortimer et al., 2016). Finally, architectural design through web geometry can affect vibrational propagation (Masters, 1984; Mortimer, 2017); radial threads with more web junctions will have more severe vibration attenuation than those with fewer junctions, for example (Masters, 1984). Figure 18 below links the control mechanisms used by spiders to change web material properties to their biological relevance.
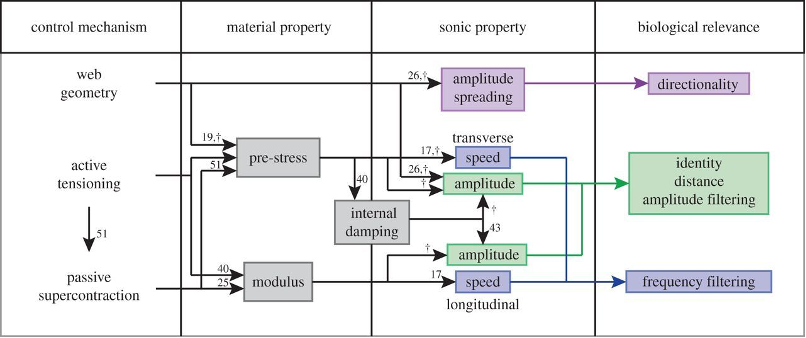
Fig. 18 Linking control mechanisms used by the spider to the material properties being manipulated. By changing the silk's properties, spiders “tune” their webs for biologically relevant signals (i.e., struggling prey, courtship signals, indicators of predators, etc.) (Mortimer et al., 2016).
It is precisely the adaptive nature of silk, allowing immense control over vibration propagation, that has enabled the success of web-weavers (Su et al., 2018). Using up to eight unique silk types (Su et al., 2018), spiders tune the biomaterial and mechanical properties of their webs to adapt to current conditions (Miller & Mortimer, 2020), amplifying (through resonance) or damping vibrations according to their frequency (Mortimer, 2019; Mortimer et al., 2016); this behavior is called frequency filtering. The following subsections examine how web-weavers use resonance and frequency filtering for survival and reproduction.
Prey capture
The most pertinent role of resonance in web-weaver survival is its use in capturing prey. In the web, massive bodies (i.e., the spider, captured prey, or foreign particles) can be approximated by a mass-spring system with silk threads acting as the spring. This approximation allows one to derive a formula for the natural frequency of objects in the web based on their mass. First, we consider the relationship between angular frequency, measured in radians/second (rad/s), and regular frequency, measured in Hz using Formula 16 (Brown, n.d.):

where f is frequency, ω is angular frequency, and 2π is the number of radians in a period of oscillation (by definition).
Now, Formula 17 considers how angular frequency is determined by the physical properties of the mass and spring (Brown, n.d.):

where k is the spring constant (force required per unit length to extend the silk thread), or stiffness, and m is the mass of the body.
If Formula 17 is substituted into Formula 16, we obtainFormula 18:

Again, this formula assumes a negligible effect of attenuation on the natural frequency. The result indicates that the natural frequency of a body in the web is only affected by the stiffness of the silk threads and the mass of the body. Thus, based on silk stiffnesses for most Araneae species and the expected mass of common prey, one can determine the approximate range of relevant natural frequencies that web-weavers might use for detecting ensnared prey through resonance. Airborne prey are conservatively expected to make vibrations in the range of 100 to 1000 Hz (Barth et al., 1988; Mortimer, 2019; Naftilan, 1999), while prey ensnared by the web are calculated to vibrate at frequencies below 50 Hz (Frohlich & Buskirk, 1982). Notably, for species such as Hololena curta (Naftilan, 1999), Octonoba sybotides (Watanabe, 2000), Coelotes Terrestris (Parry, 1965), and many other web-weavers (Frohlich & Buskirk, 1982), resonance is an important feature in web mechanics for frequencies below 50 Hz, and spiders actively tune the web to resonate bodies with natural frequencies in this range (Naftilan, 1999). This demonstrates that spiders use resonance to amplify vibrations from struggling prey, making it a crucial physical phenomenon for spider prey acquisition (Naftilan, 1999; Watanabe, 2000).
As Frolich and Buskirk note (1982), webs are like “a microphone”, providing “nearly constant amplification across the insect frequency range”. However, frequencies over ~ 1000 Hz, the upper limit of common insect vibration frequencies, experience significant attenuation (Frohlich & Buskirk, 1982). The range of vibrations capable of resonance in the web strongly aligns with the range of possible vibrations created by insect targets of predation. While web-tuning in normal conditions only allows resonance of vibrations under ~ 1000 Hz, in some situations, the spider will modify the tuning to amplify high frequency signals (Watanabe, 2000). For instance, in times of hunger, Octonoba sybotides will increase the tension in radial threads of its web so that the web can resonate the higher natural frequencies of less massive prey (Watanabe, 2000); radial webs are plucked by the spider, sending vibrations that hit and reflect off of small prey. These vibrations amplify through resonance, allowing the spider to detect and locate prey (Klärner & Barth, 1982; Miller & Mortimer, 2020;Mortimer et al. 2013, p. 43). Fundamentally, the spider uses a substrate-borne echolocation, as well as vibration resonance, to locate prey during periods of hunger. This example demonstrates he versatility of the web again, enabling highly adaptive behaviour for web-weaving spiders.
Courtship
Similar to methods of predation, spider mating strategies fall into two main species-specific categories: visual displays (used more by diurnal spiders) and vibrational displays (the primary courtship technique of nocturnal spiders, given their more rudimentary visual systems) (Wignall & Herberstein, 2013b; Morehouse et al., 2017). From an evolutionary lens, it might seem improbable that spiders would develop vibrational courtship displays rather than simply using visual modes; vibrations are limiting due to physical constraints such as energy loss and information distortion (Mortimer, 2017). However, visual displays have equally problematic disadvantages, such as the attraction of Araneae predators (Hoefler et al., 2008). For example, Pardosa milvina, a small wolf spider species, was observed to suffer higher levels of predation based on the frequency of visual sexual displays (Hoefler et al., 2008). Thus, many wolf spiders have developed “multimodal” courtship behaviours, using both vibrations and visual displays, in order to minimize the drawbacks of both techniques (Sun et al., 2021; Vaccaro, Uetz, & Roberts, 2010). Most nocturnal spiders, however, tend to rely primarily if not solely on vibrational pre-copulation courtship displays; they employ resonance to amplify signals in order to demonstrate sexual fitness (Mortimer, 2019; Wignall & Herberstein, 2013b).
Species in the Cupiennius genus use both broadband and narrowband frequencies during courtship (Mortimer, 2017); the specific frequency ranges can be used to resonate certain harmonics to enable mates to differentiate signals of struggling prey from courtship displays (Frohlich & Buskirk, 1982). Most displays are species-specific low-frequency vibrations, often intermediate between background noise and prey vibrations (Barth et al., 1988). Cupiennius spiders have male dominant peaks at 75 Hz and 115 Hz, and female dominant frequencies anywhere from 20 Hz to 50 Hz (Barth et al., 1988). Generally, the most important frequency ranges for web-weaving spiders are well below 50 Hz in order to differentiate prey from conspecifics (Frohlich & Buskirk, 1982). The natural frequency of spiders themselves usually appears in this domain (Frohlich & Buskirk, 1982); Figure 19 below shows resonance peaks for a spider in its web stimulated at a range of frequencies. Values over 1.0 suggest amplification of a source vibration (resonance); evidently, the natural frequency of most spiders is just under 10 Hz, according to the plot. Thus, spiders vibrate potential mates' webs precisely at the natural frequency of the mate itself, physically amplifying the sway of the mate in its own web; behavioral observations suggest that spiders tug or jerk on mates' webs to produce these low-frequency signals (Frohlich & Buskirk, 1982). In Argiope spiders, these courtship “shudders” have been shown to delay female predatory behaviour, lowering the instances of pre-copulatory cannibalism (which is a common trait in species across the Araneae order) (Wignall & Herberstein, 2013a). Thus, the efficacy of vibratory courtship signals at disabling female aggression has effectively become an indicator of male fitness.
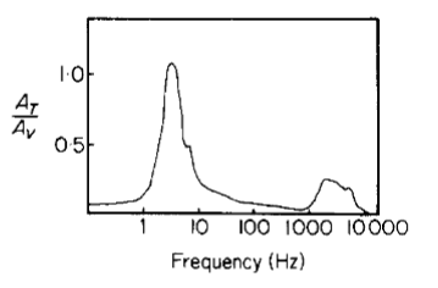
Fig. 19 Amplitude of web motion relative to source amplitude; values greater than 1.0 suggest resonance (Frohlich & Buskirk, 1982).
Summary
This section has examined the multifunctionality of resonance in the spider web for web-weaver food collection, courtship, and general survival. The highly adaptable yet mechanically resilient nature of the web allows spiders to adjust to a variety of environmental conditions, such as low food supply, rain and humidity, strong winds, and harsh web impacts. The web's chemical, mechanical, and geometric complexity allows web-weavers to differentiate prey, conspecifics, and environmental vibrations, selectively resonating or attenuating signals based on biological relevance. Furthermore, the spider actively “tunes” its web, manipulating its properties to perfect its propagation of vibrations. The spider web is an elegant example of an extended phenotype, expanding the spider's sensory space through vibration and resonance.
Conclusion
Resonating devices have essential and varied functions within the animal kingdom, from echolocation and predation to courtship and communication. In this paper, four examples were discussed. To begin, the review examined how cicadas use tandem resonators to amplify small clicks from their body to a song which rivals much larger animals. Next, the vocal cords and larynx of lions were examined to understand how lions produce their iconic, low-frequency roars. Following this, a review of the resonators found in the ears and larynxes of bats was discussed to analyze how they are such precise and effective hunters. Finally, an investigation was conducted into how web-weaving spiders use resonance within their webs to echolocate and perform courtship displays.
Despite the variety in the function of these devices, there are common themes within their structural design; each example must abide by the same fundamental physical constraints to operate effectively. For example, Helmholtz resonance is used in both the vocal tract of bats and in the abdomens of cicadas. Harmonic series, standing waves, and interference are discussed in all of the examples in this review. This is a sensible result given that all animals must obey the same physical laws, and when faced with similar problems in their environment, the same optimal solutions tend to arise. Thus, this discussion of resonating devices contributes to a larger examination of the omnipresence of convergent evolution. This speaks volumes about evolution itself, truly solidifying it as a unifying theme in biology. It is important to remember, as future biologists, bioengineers, and physicists, that nature has developed eloquent and highly efficient solutions to many problems that humans may one day face as well.
References
Barth, F. G., Bleckmann, H., Bohnenberger, J., & Seyfarth, E.-A. (1988). Spiders of the genus Cupiennius Simon 1891 (Araneae, Ctenidae). Oecologia, 77(2), 194-201. https://doi.org/10.1007/BF00379186
Baumjohann, W., Treumann, R. A., Georgescu, E., Haerendel, G., Fornacon, K.-H. ., & Auster, U. (1999). Waveform and packet structure of lion roars. Annales Geophysicae, 17(12), 1528–1534. doi.org/10.1007/s00585-999-1528-9
Berg, R. E. (2022). Sound – Helmholtz resonator. In The New Encyclopedia Britannica (15th ed.). Encyclopedia Britannica. www.britannica.com/science/sound-physics/The-ear-as-spectrum-analyzer
Britannica, T. Editors of Encyclopaedia (2011, January 13). Fresnel lens. Encyclopedia Britannica. https://www.britannica.com/technology/Fresnel-lens
Britannica, T. Editors of Encyclopaedia (2022, September 30). Resonance. Encyclopedia Britannica. https://www.britannica.com/science/resonance-vibration
Brown, R. G. (no date). Introductory Physics: Elementary Mechanics [Lecture notes]. Duke University Physics Department. https://webhome.phy.duke.edu/~rgb/Class/intro_physics_1/intro_physics_1.pdf
Cassano, D. (2020). Why is a lion's roar so loud? – Denise Cassano Illustration. Denise Cassano. denisemariecassano.com/why-is-a-lions-roar-so-loud/
Fornacon, K., Auster, H. U., Georgescu, E., Baumjohann, W., Glassmeier, K., Haerendel, G., Rustenbach, J., & Dunlop, M. (1999). The magnetic field experiment onboard Equator-S and its scientific possibilities. Annales Geophysicae. CiteSeer. citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.371.5922
Frohlich, C., & Buskirk, R. E. (1982). Transmission and attenuation of vibration in orb spider webs. Journal of Theoretical Biology, 95(1), 13-36. https://doi.org/https://doi.org/10.1016/0022-5193(82)90284-3
Garwood, R. J., Dunlop, J. A., Selden, P. A., Spencer, A. R., Atwood, R. C., Vo, N. T., & Drakopoulos, M. (2016). Almost a spider: a 305-million-year-old fossil arachnid and spider origins. Proceedings. Biological sciences, 283(1827), 20160125. https://doi.org/10.1098/rspb.2016.0125
Grinnell, J., & McComb, K. (2001). Roaring and social communication in African lions: the limitations imposed by listeners. Animal Behaviour, 62(1), 93–98. doi.org/10.1006/anbe.2001.1735
Hemiptera. (1911). In The Encyclopaedia Britannica: A Dictionary of Arts, Sciences, Literature and General Information (11th ed., pp. 259-263). Encyclopedia Britannica.
Herbst, C.T. (2016). Biophysics of Vocal Production in Mammals. Vertebrate Sound Production and Acoustic Communication, Springer Handbook of Auditory Research, 53, 159-189. doi.org/10.1007/978-3-319-27721-9_6
Hoefler, C. D., Persons, M. H., & Rypstra, A. L. (2008). Evolutionarily costly courtship displays in a wolf spider: a test of viability indicator theory. Behavioral Ecology, 19(5), 974-979. https://doi.org/10.1093/beheco/arn055
Jones, G. (2005). Echolocation. Current Biology, 15(13), 488. doi.org/10.1016/j.cub.2005.06.051
Jones, G., & Holderied, M. W. (2007). Bat echolocation calls: adaptation and convergent evolution. Proceedings of the Royal Society, 274(1612), 905–912. doi.org/10.1098/rspb.2006.0200
Kaston, B. J. (1964). The Evolution of Spider Webs. American Zoologist, 4(2), 191–207. http://www.jstor.org/stable/3881292
Keeley, B. W., Keeley, A. T. H., Houlahan, P., & Fenton, B. (2018). Ridge number in bat ears is related to both guild membership and ear length. Plos One, 13(7). doi.org/10.1371/journal.pone.0200255
Klärner, D., & Barth, F. G. (1982). Vibratory signals and prey capture in orb-weaving spiders (Zygiella x-notata, Nephila clavipes; Araneidae). Journal of comparative physiology, 148(4), 445-455. https://doi.org/10.1007/BF00619783
Knierim, J. (n.d.). Chapter 1: Motor Units and Muscle Receptors. Neuroscience Online. nba.uth.tmc.edu/neuroscience/s3/chapter01.html
Kuc, R. (2009). Model predicts bat pinna ridges focus high frequencies to form narrow sensitivity beams. The Journal of the Acoustical Society of America, 125(5), 3454–9. doi.org/10.1121/1.3097500
Landolfa, M. A.; Barth, F. G. (1996). Vibrations in the orb web of the spider Nephila clavipes: cues for discrimination and orientation. Journal of Comparative Physiology A, 179 (4), 493-508. DOI: 10.1007/BF00192316.
Laver, J. (1993). Principles of phonetics (Cambridge Textbooks in Linguistics). Cambridge University Press.
Lawrence, B. D., & Simmons, J. A. (1982). Echolocation in bats: the external ear and perception of the vertical positions of targets. Science, 218(4571), 481–483. www.science.org/doi/10.1126/science.7123247
Lindsey, P. (2021). The Complexity of Lion Roars. Lion Recovery Fund. www.lionrecoveryfund.org/stories/the-complexity-of-lion-roars/#:~:text=Lions%20roar%20more%20when%20wind
Liu, Y., Sponner, A., Porter, D., & Vollrath, F. (2008). Proline and Processing of Spider Silks. Biomacromolecules, 9(1), 116-121. https://doi.org/10.1021/bm700877g
Lohrey, A. K., Clark, D. L., Gordon, S. D., & Uetz, G. W. (2009). Antipredator responses of wolf spiders (Araneae: Lycosidae) to sensory cues representing an avian predator. Animal Behaviour, 77(4), 813-821. https://doi.org/https://doi.org/10.1016/j.anbehav.2008.12.025
Mariano-Martins, P., Lo-Man-Hung, N., & Torres, T. T. (2020). Evolution of Spiders and Silk Spinning: Mini Review of the Morphology, Evolution, and Development of Spiders' Spinnerets [Mini Review]. Frontiers in Ecology and Evolution, 8. https://doi.org/10.3389/fevo.2020.00109
Masters, W. M. (1984). Vibrations in the Orbwebs of Nuctenea sclopetaria (Araneidae): I. Transmission through the Web. Behavioral Ecology and Sociobiology, 15(3), 207–215. http://www.jstor.org/stable/4599721
Metzner, W., Müller, R. (2016). Ultrasound Production, Emission, and Reception. Bat Bioacoustics, Springer Handbook of Auditory Research, 54, 55-93. doi-org.proxy3.library.mcgill.ca/10.1007/978-1-4939-3527-7_3
Miller, T. E., & Mortimer, B. (2020). Control vs. Constraint: Understanding the Mechanisms of Vibration Transmission During Material-Bound Information Transfer [Review]. Frontiers in Ecology and Evolution, 8. https://doi.org/10.3389/fevo.2020.587846
Morehouse, N. I., Buschbeck, E. K., Zurek, D. B., Steck, M., & Porter, M. L. (2017). Molecular Evolution of Spider Vision: New Opportunities, Familiar Players. The Biological Bulletin, 233(1), 21-38. https://doi.org/10.1086/693977
Mortimer, B. (2017). Biotremology: Do physical constraints limit the propagation of vibrational information? Animal Behaviour, 130, 165-174. https://doi.org/https://doi.org/10.1016/j.anbehav.2017.06.015
Mortimer, B. (2019). A Spider's Vibration Landscape: Adaptations to Promote Vibrational Information Transfer in Orb Webs. Integrative and Comparative Biology, 59(6), 1636-1645. https://doi.org/10.1093/icb/icz043
Mortimer, B., Gordon, S., Drodge, D., Siviour, C., Windmill, J., Holland, C., and Vollrath, F. (2013). Sonic Properties of Silks. XIV International Conference on Invertebrate Sound and Vibration [Conference notes]. University of Strathclyde, Glasgow. http://www.isv2013.org/ISV_files/ISV2013%20Abstract%20Book%20Final_web.pdf
Mortimer, B., Soler, A., Siviour, C. R., & Vollrath, F. (2018). Remote monitoring of vibrational information in spider webs. Die Naturwissenschaften, 105(5-6), 37. https://doi.org/10.1007/s00114-018-1561-1
Mortimer, B., Soler, A., Siviour, C. R., Zaera, R., & Vollrath, F. (2016). Tuning the instrument: sonic properties in the spider's web. Journal of the Royal Society, Interface, 13(122), 20160341. https://doi.org/10.1098/rsif.2016.0341
Mortimer, B., Soler, A., Wilkins, L., & Vollrath, F. (2019). Decoding the locational information in the orb web vibrations of Araneus diadematus and Zygiella x-notata. Journal of the Royal Society, Interface, 16(154), 20190201. https://doi.org/10.1098/rsif.2019.0201
Naftilan, S. A. (1999). Transmission of vibrations in funnel and sheet spider webs. International Journal of Biological Macromolecules, 24(2), 289-293. https://doi.org/https://doi.org/10.1016/S0141-8130(98)00092-0
Parry, D. A. (1965). The Signal Generated by an Insect in a Spider's Web. Journal of Experimental Biology, 43(1), 185-192. https://doi.org/10.1242/jeb.43.1.185
Römer, L., & Scheibel, T. (2008). The elaborate structure of spider silk: structure and function of a natural high performance fiber. Prion, 2(4), 154–161. https://doi.org/10.4161/pri.2.4.7490
Ross, A. (2017). Insect Evolution: The Origin of Wings. Current Biology, 27(3), R113-R115. https://doi.org/https://doi.org/10.1016/j.cub.2016.12.014
Scheel, D., & Packer, C. (1991). Group hunting behaviour of lions: a search for cooperation. Animal Behaviour, 41(4), 697–709. doi.org/10.1016/s0003-3472(05)80907-8
Sensenig, A., Agnarsson, I., and Blackledge, T. A. (2010). Behavioural and biomaterial coevolution in spider orb webs. Journal of Evolutionary Biology, 23(9), 1839-1856. https://doi.org/https://doi.org/10.1111/j.1420-9101.2010.02048.x
Simmons, J. A. (1973). The resolution of target range by echolocating bats. The Journal of the Acoustical Society of America, 54(1), 157–73. doi.org/10.1121/1.1913559
Simmons, J. A., & Stein, R. A. (1980). Acoustic imaging in bat sonar: echolocation signals and the evolution of echolocation. Journal of Comparative Physiology, 135(1), 61–84. doi.org/10.1007/BF00660182
Stafstrom, J. A., Menda, G., Nitzany, E. I., Hebets, E. A., & Hoy, R. R. (2020). Ogre-Faced, Net-Casting Spiders Use Auditory Cues to Detect Airborne Prey. Current biology : CB, 30(24), 5033–5039.e3. https://doi.org/10.1016/j.cub.2020.09.048
Stokes, D. R. & Josephson, R. K. (2004). Power and control muscles of cicada song: structural and contractile heterogeneity. Journal of Comparative Physiology A, 190, 279-290. doi.org/10.1007/s00359-003-0490-3
Su, I., Qin, Z., Saraceno, T., Krell, A., Mühlethaler, R., Bisshop, A., & Buehler, M. J. (2018). Imaging and analysis of a three-dimensional spider web architecture. Journal of the Royal Society, Interface, 15(146), 20180193. https://doi.org/10.1098/rsif.2018.0193
Sun, Y., Brandt, E. E., Elias, D. O., Rosenthal, M., & Kamath, A. (2021). Jumping Spiders (Habronattus clypeatus) Exhibit Substrate Preferences that Partially Maximize Vibration Transmission Efficiency. Journal of Insect Behavior, 34(4), 151-161. https://doi.org/10.1007/s10905-021-09777-x
Suthers, R. A., & Fattu, J. F. (1973). Mechanisms of sound production by echolocating bats. American Zoologist, 13(4), 1215–1226. doi.org/10.1093/icb/13.4.1215
Suthers, R. A., Hartley, D. J., & Wenstrup, J. J. (1988). The acoustic role of tracheal chambers and nasal cavities in the production of sonar pulses by the horseshoe bat, rhinolophus hildebrandti. Journal of Comparative Physiology A : Sensory, Neural and Behavioral Physiology, 162(6), 799–813. doi.org/10.1007/BF00610969
The Efficient Engineer. (2020, October 6). Understanding Bernoulli's Equation [Video]. YouTube. www.youtube.com/watch?v=DW4rItB20h4
Titze, I. (2012). Why lions roar like babies cry. Physics World, 25(11), 52–53. doi.org/10.1088/2058-7058/25/11/43
University of Caifornia, Los Angeles (no date). Physics 6B Lab Experiment 2: Standing Waves [Lecture Notes]. UCLA Physics and Astronomy Department. https://demoweb.physics.ucla.edu/sites/default/files/Physics6B_Exp2.pdf
University of Utah (2011). Born to roar: Lions' and tigers' fearsome roars are due to their unusual vocal cords. ScienceDaily. www.sciencedaily.com/releases/2011/11/111102190012.htm
Urone, P. P., Hinrichs, R., Dirks, K., Sharma, M. (no date). College Physics. OpenStax. https://pressbooks.uiowa.edu/clonedbook/front-matter/preface-to-college-physics/
Vaccaro, R., Uetz, G. W., & Roberts, J. A. (2010). Courtship and mating behavior of the wolf spider Schizocosa bilineata (Araneae: Lycosidae). The Journal of Arachnology, 38(3), 452-459, 458. https://doi.org/10.1636/Hi09-115.1
Vollrath, F., & Selden, P. (2007). The Role of Behavior in the Evolution of Spiders, Silks, and Webs. Annual Review of Ecology, Evolution, and Systematics, 38(1), 819-846. https://doi.org/10.1146/annurev.ecolsys.37.091305.110221
Walcott, C., & van der Kloot, W. G. (1959). The physiology of the spider vibration receptor. Journal of Experimental Zoology, 141(2), 191-244. https://doi.org/https://doi.org/10.1002/jez.1401410202
Watanabe T. (2000). Web tuning of an orb-web spider, Octonoba sybotides, regulates prey-catching behaviour. Proceedings. Biological sciences, 267(1443), 565–569. https://doi.org/10.1098/rspb.2000.1038
Wignall, A. E., & Herberstein, M. E. (2013). Male courtship vibrations delay predatory behaviour in female spiders. Scientific Reports, 3(1), 3557. https://doi.org/10.1038/srep03557
Wignall, A. E., & Herberstein, M. E. (2013). The influence of vibratory courtship on female mating behaviour in orb-web spiders (Argiope keyserlingi, Karsch 1878). PloS one, 8(1), e53057. https://doi.org/10.1371/journal.pone.0053057
Wolfe, J. (2005). Helmholtz Resonance. The University of New South Wales – Music Acoustics. newt.phys.unsw.edu.au/jw/Helmholtz.html
Young, D. & Bennet-Clark, H. C. (1995). The role of the timbal in cicada sound production. Journal of Experimental Biology, 198(4), 1001-1019. doi.org/10.1242/jeb.198.4.100