Numerical Modeling of Butterfly Scale Structure and a Few of its Physical Properties
Eve Barrette-Vanasse, Anne Laurin, Rus Trana, Jun Xiao
Abstract
Although butterflies are some of the most delicate organisms on the planet, they have managed to achieve remarkable success in their survival. Much of this success is owed to the unique chitinous scales coating the body of butterflies, especially the wings. These scales produce self-cleaning and hydrophobic properties allowing the wings to function under any conditions due to unique ridge spacing. Additionally, thin layer diffraction (a form of coherent scattering) is enabled by scale microstructure to produce the vibrant colors butterflies are known for. Without scales, butterflies and moths would be dull, dirty, and dangerously close to extinction.
Introduction
Butterflies are the fourth largest order of described organisms with 10% of the total described species falling within the order (Scoble, 1992). Due to their small size and poor defenses, they serve as an important food source for many animals such as birds and amphibians. Among the more than 180,000 species there are a few common characteristics that have allowed them to succeed despite the many predation risks they face. Most visible are the large wings that make butterflies competent fliers, allowing them to avoid many predators and access food sources. The proboscis of butterflies and moths is also a defining trait. It has evolved into many different shapes granting access to otherwise inaccessible food sources. For example, many plants have evolved side by side with moths to possess uniquely shaped flowers that only the proboscis of one butterfly variety can reach the nectar of (Scoble, 1992). This ensures minimal competition for the butterfly's food source and reliable pollination for the plant. A less known but still highly useful adaptation is the layer of scales that covers the entire insect. The scales aid butterflies in shedding dirt and water that could inhibit their flying capabilities while also having unique microstructures that produce the vibrant colors of butterfly wings.
A majority of the surface area of a butterfly consists of its wings. As a result, much of the debris falling on the organisms collides with the wings. The body plan of these insects does not allow them to easily access their wings with other appendages, therefore it is almost impossible for cleaning to occur. Butterfly wings must have self-cleaning properties to ensure they remain useful. Unsurprisingly, unique scale microstructures have been found that display hydrophobic and dirt repelling properties keeping the wings clean and functional. Additionally, the large area of wings makes them conspicuous. This provides a large canvas for intimidation, camouflage, and signaling to occur. Pigment is used in certain species of butterflies. However, the most striking colors are created through structural coloration. This is the use of microscopic structures that alter the behavior of visible light to produce colors (Benedeck, 1971). Butterflies rely on different microstructures in-between species, however thin film optics using coherent scattering are the most common varieties.
Modeling for ridge self-cleaning
Butterfly scales are made of ridges, ribs, and trabeculae joining the upper and lower laminae, as depicted in Figure 1 (Köchling et al., 2020).

Fig. 1 Ridges, ribs, and trabeculae on butterfly scales are shown: d is the distance between two ridges and h is the height of a ridge (Adapted from Köchling et al., 2020).
Most butterflies' scales belong to two types: cover and ground scales. Cover scales slightly overlap ground scales, which have denser ridges (see Figure 2). For other butterflies, like the G. Agamemnon and the Greta oto, scales are hair-like, as shown in Figure 2. Butterflies with the latter type of scales cannot have the ridges on their scales measured and are therefore not considered for the rest of this analysis (Köchling et al., 2020).

Fig. 2 A shows the ground (base) and cover scales. Ground scales have denser ridges compared to cover scales. B shows scales on G. Agamemnon resembling hair. Scanning Electron Microscopy (Adapted from Köchling et al., 2020).
The height (h) of a ridge can be measured along with the distance (d) between two consecutive ridges on cover scales by first imaging them with scanning electron microscopy and transmission electron microscopy. The ratio of these two measurements is defined by r=h/d. For ten butterfly species, the height and distance of ridges were examined, and it was found that they obey a linear scaling law. In fact, h=0.383d is the resulting equation for this scaling law. Also, none of the ridges on the different butterfly species have a ratio larger than 0.5, which can be seen in Figure 3 and means that the distance between two consecutive ridges never exceeds double their height (Köchling et al., 2020).
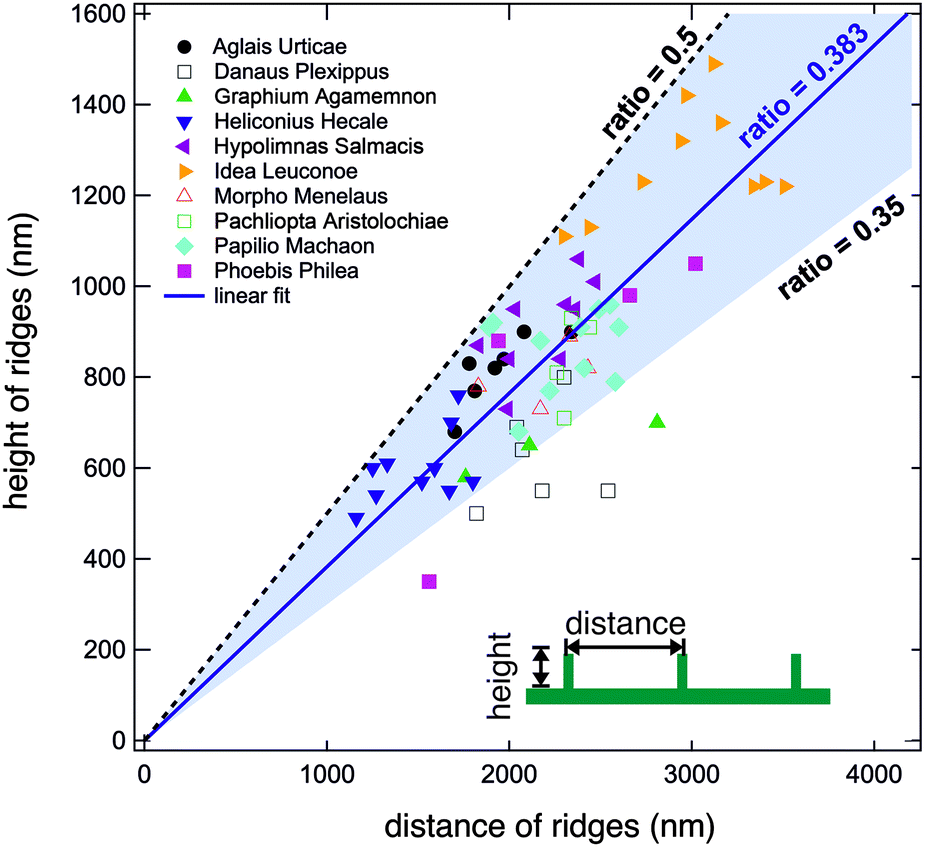
Fig. 3 Graph of the height against the distance of ridges. The blue shaded area in the graph indicates that most of the ratios are valued between 0.35 and 0.5. No ratio goes beyond 0.5 delimited by the black dotted line (Köchling et al., 2020).
The scaling law proves to be effective when looking at a specific type of self-cleaning. When a butterfly moves its wings, it creates an air stroke that brushes off dirt stuck between ridges. This is called dry self-cleaning. The scaling law is only useful for small dirt particles that get lodged between ridges because bigger particles would only be in contact with the top of the ridges without falling between them and getting stuck. On one hand, if the ratio r=h/d is significantly below 0.5, meaning that the ridge height is small compared to the distance separating ridges, then small dirt particles will not get stuck. On the other hand, if the ratio is above 0.5, small particles can get lodged between ridges (Köchling et al., 2020). The link between self-cleaning and ridge dimensions can be seen in figure 4. However, none of the observed butterfly species have a ratio greater than 0.5, which indicates that a ratio greater than 0.5 is indeed not beneficial to the butterfly.

Fig. 4 A depicts when the h/d ratio is relatively small, small particles do not get stuck between riblets. B depicts when this ratio is greater than 0.5 particles get stuck between ridges. Bigger particles are not affected by either case A or B, as they stay put on the top of ridges (Adapted from Köchling et al., 2020).
Mathematical modeling of the hydrophobic mechanism of butterfly wings
Butterfly wings display hydrophobic properties. These prevent the butterfly wing from getting wet so that the wings can remain light enough for the butterfly to spend less energy on flapping them. One hypothesis suggests that the hydrophobic effect is due to the shape of the butterfly scale (Fang et al., 2007). More precisely, when water droplets fall on the wing, there are regions of air between the ribs of the scale stopping water from contacting the region between the scale's ribs by the air pressure as well as the surface tension force of the water itself (Fang et al., 2007). This causes a reduction in both the contact area and adhesion between water and scale; thus, the water droplets can fall off from the scale more easily than from a flat platform. Fang's team aimed to find an accurate mathematical model to explain how the butterfly scales lead to the hydrophobic effect (Fang et al., 2007).
Cassie previously claimed a model for describing the contact angle between the liquid and non-smooth surfaces, shown in equation (1) (Cassie, A. B., & Baxter, S., 1944). The work of Fang's team was mainly based on Cassie's model (Cassie, A. B., & Baxter, S., 1944).
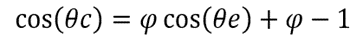
(1)
Θc stands for the contact angle between the liquid and the surface made up of air and solid (Cassie, A. B., & Baxter, S., 1944). Θe stands for the contact angle between the liquid and the surface if the surface is flat. Φ stands for the area ratio of the solid on the surface and is from 0 to 1 (Cassie, A. B., & Baxter, S., 1944). If the Θc is higher, there is a higher tendency for the liquid droplet to be a sphere on the surface. As the droplets can be easier to roll out if they are more spherical, a higher Θc corresponds to a higher hydrophobicity of the butterfly wing surface.
Firstly, Fang's team hypothesized that identical butterfly wing scales are in a close, regular, and flat arrangement, meaning no ribs on the scales (Fang et al., 2007). They assumed the length and width of scales and the distance between scales as a, b, and c (Fang et al., 2007). The hypothesis is shown in Figure 5. Under that hypothesis, the theoretical contact angle (Θc) between the liquid and the wing surface can be expressed as the equation (2) (Fang et al., 2007).
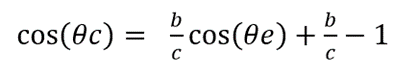
(2)

Fig. 5 Visualization for the first hypothesis of Fang's team (Fang et al., 2007).
The model shows that, if the scale's width becomes shorter and the distance between scales becomes longer, the contact angle between the fluid and the wing surface is larger, reflecting the higher hydrophobicity of the wing surface (Fang et al., 2007). However, Fang's team found that the theoretical contact angle of 29 butterfly species (100.3°―117.1°) from this model is lower than the observed data (136.3o-156.6o), meaning the hydrophobicity is not solely attributable to the scales' size and arrangement (Fang et al., 2007).
To determine the effect of the scale's gibbosities on the butterfly wing's hydrophobicity, Fang's team hypothesizes that the butterfly scales have no space between them and contain regularly aligned gibbosities (triangle-like in the cross-section) on the scales' surface (Fang et al., 2007). The height and width of gibbosities and the distance between gibbosities can be written as d, e, and f respectively (Fang et al., 2007). The visualization for the hypothesis is shown in Figure 6 (Fang et al., 2007). Under this condition, the model can be revised to equation (3) (Fang et al., 2007).
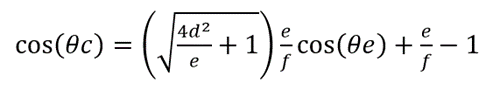
(3)

Fig. 6 The diagram shows the second hypothesis of Fang's team. It is noticeable that there are air regions between gibbosities that water cannot enter (Fang et al., 2007). The air regions exist because of the air pressure.
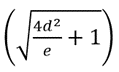
stands for a roughness factor and represents the ratio of the actual area that the surfaces on gibbosities have contact with the liquid to the width of gibbosities (Fang et al., 2007). The calculation results of the theoretical contact angles for 29 butterfly species are around 124.5o-146.9o, which are still slightly smaller than the observed contact angles (136.3o-156.6o) (Fang et al., 2007). This means that the existence of gibbosities on the butterfly scales is still not the key factor explaining the butterfly wing's hydrophobicity (Fang et al., 2007).
Then, based on Figure 7, Fang's team combined the previous two hypotheses to hypothesize that identical scales with triangular gibbosities are in regular, close, and flat arrangement, and that those gibbosities are parallel to each other and regularly aligned (Fang et al., 2007). The scales' length and width, the distance between scales, gibbosities' height, width, and the distance between gibbosities are assumed to be a, b, c, d, e, and f respectively (Fang et al., 2007). Under this hypothesis, the model is revised to equation (4) (Fang et al., 2007).

(4)

Fig. 7 The diagram shows the third hypothesis of Fang's team. This hypothesis combines the conditions of the previous two assumptions (Fang et al., 2007). There are air regions between scales and between scale's gibbosities.
The calculation results from this model only produce a relative error of between 0% and 7.23% from the observed data, showing that the third hypothesized model is comparatively accurate in describing the hydrophobicity of butterfly wings' scales (Fang et al., 2007). Once can let α and β be quantities such that they follow the equation (5) and (6) respectively (Fang et al., 2007):

(5)

(6)
The α reflects the size of the surface area on a gibbosity, while β reflects the ratio of solid area to the total area of contact between liquid and the wing surface. In the model, when α and β decrease, the contact angle Θc increases (Fang et al., 2007). This reflects that, if the scale width, gibbosity height, and obesity width become smaller, and scale distance and gibbosity distance become larger, the contact angle will increase, meaning higher hydrophobicity (Fang et al., 2007). Therefore, the model of Fang's team reveals the mechanisms behind butterfly wing hydrophobicity (Fang et al., 2007.)
To conclude, the model of Fang's team shows that the co-effects of size and arrangement of scales and their gibbosities is the key factor explaining the hydrophobicity of the butterfly wing scales (Fang et al., 2007).
Fourier transform modeling of butterfly scales
Colors are caused by light of varying wavelengths. Altering the output spectrum of light can be done through many physical mechanisms that can be divided into two main categories: coherent and incoherent scattering (Prum et al. 2006). The mechanism used in butterfly scales was unknown, due to complications accurately modeling the relationship between the physical structure of the scales and the resultant color. Figure 8 illustrates many of the vibrant iridescent colors butterflies and certain diurnal moths are capable of producing.

Fig. 8 Photographs of butterflies and some moths displaying iridescent behavior in their scales (Prum, et al, 2006).
To accurately understand the mechanics of how this process occurs, much higher magnification images of the butterflies are required. Specifically, individual scale morphology and overlapping is useful. Light microscope images of scales are shown below in Figure 9.

Fig. 9 Light microscope images at 65x of butterfly species shown in Figure 8 (Prum et al, 2006).
Figure 9 describes the morphology of the scales on a microscale, however the exact mechanism of color generation is still unclear at this resolution. More complex analytical models are required to understand the color production method of the butterfly scale. By creating Fourier series representations of the light refracted from the scales and using Bragg's reflection principle the final wavelength of light can be estimated (Benedeck, 1971).
Fourier transforms are one of the most powerful mathematical analysis tools ever developed. They allow any input with a finite energy to be represented as a function in the frequency domain. This frequency domain function represents the frequency and amplitude of complex sinusoids (Briggs and Henson, 1995). This is useful for performing computational analysis because there are many properties of these sinusoidal functions that simplify analyses. Fourier series can have an infinite number of terms, however for engineering applications a finite number of terms produces acceptable low error (Briggs and Henson, 1995). Converting the refraction behavior into its Fourier representation is difficult for data as large and complex as high-resolution images is unfeasible for manual calculations and older slower algorithms. This has given rise to newer computational algorithms that can take input signals and convert them to their Fourier transform representation with certain simplifications that significantly reduce computation time. One of the most common is the 2-D fast Fourier transform that has been implemented in many computer programs such as MATLAB and python.

(7)
Eq. 7 The discrete time Fourier transform relationship where Xk represents the coefficients, and N is the sample size (Briggs and Henson, 1995).
These algorithms and computer programs can be used to easily find the Fourier representation of signals and convert them into a Fourier power spectrum. This represents how the refractive index of the scales varies with spatial variation (Prum et al., 2006). This spectrum can be used to estimate the peak hue wavelength of light output by the scales. This can be combined with expected behavior for coherent and incoherent scattering to determine which scattering method dominates. Coherent scattering is used in the scales of other vibrant insects, so it was used to estimate peak hue and compared with experimental data as shown in Table 1.

Table 1 Predicted vs. Actual Butterfly Scale Peak Hues.
The predicted values line up well with the actual values for most butterfly species. This implies that the actual action method is coherent scattering. This narrows the potential microstructures utilized by butterfly scales to interference, thin-film reflection, and diffraction (Prum et al, 2006).
Modeling of the reflectance spectra of butterfly scales
Butterflies have evolved various bright coloration patterns. These mostly originate from the structure of the scales on their bodies rather than from pigments. This type of coloration is called “structural coloration” and it occurs in butterflies due to the optical properties of the scales' ridges (Ghiradella, 1991).
These optical mechanisms of coloration are dictated by the principles of thin-film optics, a type of coherent scattering. Butterfly scales are made of thin chitin layers and air pockets, as can be seen in Figure 10 c). As light passes through the chitin, part of it is refracted upon entry – with a given refractive index – and refracted again as it exits the chitin layer, as seen in Figure 10 b). When the thickness of the chitin layer is of order of a wavelength, the parts of light which are refracted interfere with each other, which amplifies the color reflected by the scales. The lower lamina of the scale structure reflects light once, but on the ridges of the scales, the light can be reflected multiple times and create a greater reflection through consecutive thin film interference (Lloyd, 2021).
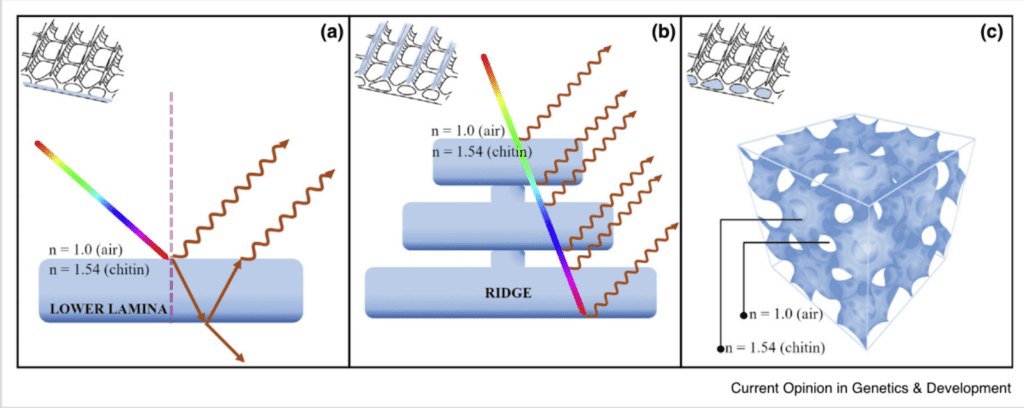
Fig. 10 Optical thin-film nanostructures of butterfly scales: A) Thin-film interference in the laminal layers of the chitin scales; B) Consecutive refraction of scales on the ridges of the scales; C) Internal three-dimensional structure of chitin scales (Lloyd, 2021).
It is known that the propagation of light through a medium is expressed through Snell's law:
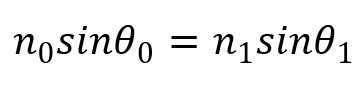
(8)
Where n0 and n1 are the refractive indices of the first and second medium, and 1 and 0 are the incident angle of the light and the angle of the light after refraction, respectively.
The reflectance spectra of chitinous optical thin films can be modeled using a classical Airy function:
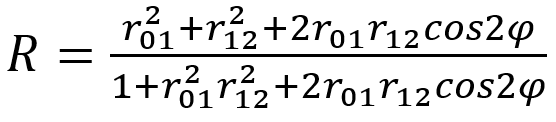
(9)
Where r01 is the refraction index for the first medium and r12 is the refraction index for the second medium that the light passes through. φ = (2p/λ)n1dcosθ1, where λ is the wavelength of the incident light (Stavenga et al., 2012).
For scales with multiple layers of chitin, a transfer matrix can be used to express the reflectance of the scales for N layers:

(10)
Where Ti and Ri are the transmittance and reflectance of layer i = 1, 2, … N.
The reflectance of the total “stack” of chitin layers is thus expressed by the product matrix:

(11)
Where R1N is the reflectance when light hits the first layer, RN1 is the reflectance when light hits the Nth layer, and T is the transmittance, which remains constant (Stavenga et al., 2018).
Different studies have compared this model's projections to experimentally collected reflectance values. For example, Figure 11 shows the theoretical projection of the reflectance of light through the butterfly scales of P. parhassus (in (A)) and the corresponding experimental projection for various incident angles 1 (Stavenga et al., 2021). It can be noted that the reflected color will vary depending on the angle of the light, as can be seen in Figure 11A, since the wavelengths of light which is more greatly reflected by the scales vary with the angle 1 (Stavenga et al., 2021).
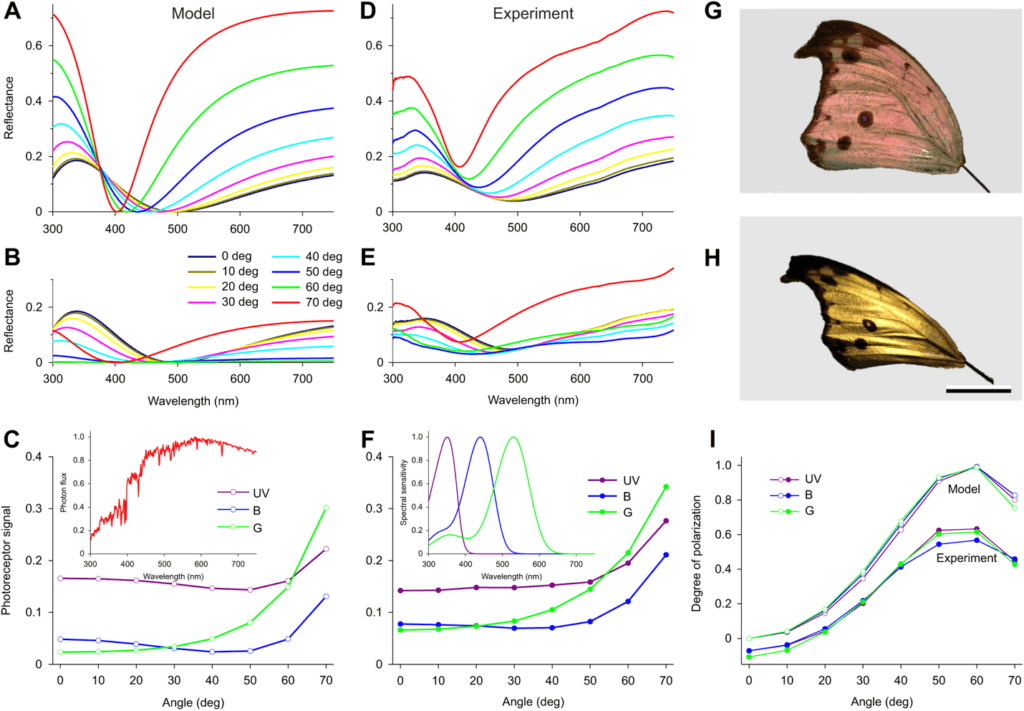
Fig. 11 Mathematical modeling of the reflectance of butterfly scales: (A) shows spectra of thin film of 160 nm thickness as a function of the incident angle of light; (B) shows reflectance of light through the butterfly scales of P. parhassus and the corresponding experimental projection for various incident angles (Adapted from Stavenga et al., 2021).
Although some species of butterflies have pigments on their wings which also alter their color, butterflies like the blue Morpho depend on their structural coloration to provide 75% of their bright coloration (See Figure 12). Other butterflies such as the Eurema lisa also have reflection spectra which reflect in the UV region of the electromagnetic spectrum, which is visible to some other species of insects and birds (cf. Figure 13) (Lloyd & Nadeau, 2021).

Fig. 12 Bright structural coloration of the Morpho butterfly (From Butterfly Identification).

Fig. 13 Coloration of the little yellow butterfly Eurema lisa which exhibits UV reflectance (Model, 2012).
Conclusion
The scaling law h = 0.383d governs the relationship between the height and distance of riblets. These specific ratios between the height and distance between riblets show to be beneficial when looking at self-cleaning. This evolutionary adaptation imparts antifouling properties on the butterfly wings, which have a large area that cannot be cleaned otherwise.
There might be water on the butterfly wings, especially during rains, making the wings heavier. As the weight of the wings increases, the energy cost for the butterfly's flight increases. Fortunately, the wing scales' hydrophobic properties allow the butterfly to avoid the above situations (Fang et al., 2007.) The hydrophobicity can be described by the mathematical model of the equation (4). The model reveals that the hydrophobic properties are because of the co-effect of size and arrangement of scales and their gibbosities (Fang et al., 2007).
Mathematical models relying on Fourier series algorithms have shown that the physical coloration in distantly related butterfly scales is produced through coherent scattering. Using this information further modeling based on thin-film optics produces highly accurate models proving the mechanism for physical coloration in butterflies is thin-film optics.
The high level of conservation in this scale structure between distantly related butterfly species implies that it provides a strong evolutionary advantage for the insects. The diurnal lifestyle of butterflies coupled with their conspicuous wings provides a strong incentive for visual signaling through wing scales. Structural coloration through thin-film optics provides an avenue for butterflies to produce this color without going through the energy intensive process of producing and maintaining pigment concentrations in their scales. The metabolic advantages of structural coloration over the pigment route could be the evolutionary drivers that have kept this structure significantly conserved amongst all butterflies.
References
Benedek, G. B. “Theory of transparency of the eye.” Applied optics 10.3 (1971): 459-473.
Briggs, W. L., & Henson, V. E. (1995). The DFT: an owner's manual for the discrete Fourier transform. Society for Industrial and Applied Mathematics.
Butterfly Identification. Blue Morpho Butterfly [Photograph]. https://www.butterflyidentification.com/blue-morpho.htm
Cassie, A. B., & Baxter, S. (1944). Wettability of porous surfaces. Transactions of the Faraday Society, 40, 546. https://doi.org/10.1039/tf9444000546
Fang, Y., Sun, G., Wang, T., Cong, Q., & Ren, L. (2007). Hydrophobicity mechanism of non-smooth pattern on surface of butterfly wing. Chinese Science Bulletin, 52(5), 711-716. https://doi.org/10.1007/s11434-007-0120-5
Ghiradella, H. (1991). Light and color on the wing: Structural colors in butterflies and moths. Applied Optics, 30(24), 3492–3500. https://doi.org/10.1364/AO.30.003492
Köchling, P., Niebel, A., Hurka, K., Vorholt, F., & Hölscher, H. (2020). On the multifunctionality of butterfly scales: a scaling law for ridges of cover scales. Faraday Discussions, 223, 195-206. https://doi.org/10.1039/d0fd00038h
Lloyd, V. J. & Nadeau, N. J. (2021). The evolution of structural colour in butterflies. Current opinions in Genetics & Development. 69, 28-34. https://doi.org/10.1016/j.gde.2021.01.004
Model, F. (2012) Eurema lisa [Photograph]. Massachussets Butterfly Club. https://www.naba.org/chapters/nabambc/construct-species-page.asp?sp=Eurema-lisa#phototable-5
Prum, R. O., Quinn, T., & Torres, R. H. (2006). Anatomically diverse butterfly scales all produce structural colours by coherent scattering. Journal of Experimental Biology, 209(4), 748-765.
Scoble, Malcolm J. The Lepidoptera. Form, function and diversity. Oxford University Press, 1992.
Stavenga, D. G. (2021). The wing scales of the mother-of-pearl butterfly, Protogoniomorpha parhassus, are thin film reflectors causing strong iridescence and polarization. Journal of Experimental Biology, 224(15), jeb242983. https://doi.org/10.1242/jeb.242983
Stavenga, D. G., Leertouwer, H. L., Meglič, A., Drašlar, K., Wehling, M. F., Pirih, P., & Belušič, G. (2018). Classical lepidopteran wing scale colouration in the giant butterfly-moth Paysandisia archon. PeerJ, 6, e4590. https://doi.org/10.7717/peerj.4590
Stavenga, D. G., Matsushita, A., Arikawa, K., Leertouwer, H. L., & Wilts, B. D. (2012). Glass scales on the wing of the swordtail butterfly Graphium sarpedon act as thin film polarizing reflectors. Journal of Experimental Biology, 215(4), 657–662. https://doi.org/10.1242/jeb.066902