Proboscis Geometry, Allometry and the Mathematical Beauty of Spirals in Nature
Han Ru Liu, Letizia Marello, Liam Sterne, Kori Zhang
Abstract
The proboscis has many functions, notably feeding and mating, making it an incredibly useful organ. This paper aims to explore its structure and study the type of relationship between its components, called an allometric relationship. Allometry also appears when studying how changes in structure affect some functions of the proboscis, such as fluid uptake rate, which can be used to predict data or behaviors of fluid-feeding insects. Furthermore, a discussion on the butterfly proboscis geometry in relation to the Fibonacci sequence and the Golden Ratio will be presented. At rest, the butterfly proboscis is coiled up into a spiral that can be modeled by the logarithmic spiral, also known as the golden spiral. This is one of many occurrences of the golden ratio in nature as it is known as nature's code; it gives balance and beauty. Mathematical beauty is a very tricky concept to define and brings a discussion on the appealing aspects of the golden ratio, and how it governs many natural mechanisms such as phyllotaxis and molecular architecture. As such, artists and architects apply this ratio to their work, from the Pyramids in Giza, to Da Vinci's famous Mona Lisa painting.
Keywords: proboscis, allometry, proboscis geometry, Fibonacci, Golden Ratio, molecular architecture.
Introduction
Mathematical and geometrical principles can be seen everywhere in nature, especially in the animal world. The structure of the proboscis in fluid-feeding insects is an example of mathematical beauty in nature and provides a very intriguing example of the curious relationships that can be found between different body parts of an animal. It is interesting to understand how changes in a part of the proboscis will affect changes in another structural characteristic. Allometry describes a disproportionate relationship between different characters: if one character increases in measurement, the other increases at a nonlinear rate. Changes in structures can also affect proboscis' functionalities like feeding, more specifically the rate of fluid uptake, feeding preferences, foraging distance and many others. This knowledge can then be applied in fields such as ecology, where predictions can be made based on known allometric relationships between certain characters thanks to mathematical functions. Mathematics can also be observed in the proboscis by analyzing the geometrical structure in itself. The divine ratio, the golden ratio, the golden spiral are all terms used to describe an ancient mathematical phenomenon that saturates natural patterns and order. All of these concepts are derived from an idea by Euclid dividing up a length (a+b) into parts as seen in Fig. 1 “b is to a as a is to a+b”. This then provides a ratio of a/b = (a+b)/a = 1.61803398875…

Fig. 1 The golden ratio derived from sectioning a length PQ.
From simple line division, many relationships in mathematics and nature have unique properties that raise questions about complex natural mechanics. To begin with, the golden ratio is a very popular irrational number; irrationality can be explained by the inability to be described as a ratio of two natural numbers. In ancient times, this idea of wonder undermined the religious admiration for arithmos, a view of the mathematical importance of whole numbers and their ratios. The mathematician Pythagoras even believed that this horrific number represented a cosmic error, and its theory was sacred. The ratio is later given the Greek letter phi, which comes from the name Phidias one of ancient Greece's most revered architects and sculptors. In honor of the golden ratio's frequent use as inspiration in art and architecture, the ratio was deemed as φ. From the ratio, many geometrical wonders can be derived, notably the rectangle. Golden rectangles are formed from sectioned lines with the larger dimension the larger section, and the smaller dimension the smaller section. If you inscribe golden rectangles in this initial rectangle and continue to do so you form the golden spiral whose increasing size follows the Fibonacci series. Moreover, the golden pentagram, a symmetrical pentagon inscribed with an equilateral star, has dimensions of the golden section.

Fig. 2 a) The golden spiral b) the golden pentagram (Luttge, 2019).
Mathematicians are not the only ones that have found fascination in this ratio. Biologists notice natural patterns in complex biological mechanisms such as plant seed dispersion, phyllotaxis as well as aesthetics in the human face. It is also used with technology to optimize aesthetics for media design.
Allometric growth
The proboscis is an essential organ for fluid-feeding insects. It consists of two C-shaped fibers, the galeae, that, joined together, form the food canal of the proboscis (Figure 3). The two are linked by rows of overlapping, fence-like dorsal and ventral legulae (Pometto, 2019).

Fig. 3 (a) Proboscis of Danaus Plexippus where the upper (ub) and lower (lb) branches of the legulae (lw) and the galeae (gw) are shown. (b) Schematic of a cross section of the proboscis showing two C-shaped galeae with lateral and median intrinsic muscles (lm and mm), nerves (ne) and tracheae (tr). The galeae are held together by overlapping dorsal legulae (dl) and interlinking ventral legulae (vl), forming a food canal (fc) (Lehnert et al., 2013).
The proboscis is composed of a hydrophilic drinking region, which represents 5-17 % of the proboscis (depending on the species), where water is attracted to the surface; and a hydrophobic non-drinking region where water is repelled from the surface (Lehnert et al., 2013). The drinking region refers to the tip of the proboscis, which is hydrophilic to assist feeding while the rest of the surface is hydrophobic.
The structure of the proboscis of fluid-feeding insects is greatly related to their feeding habits and their body size which is why it is very interesting to analyze the relationship between adult body size and the structural configurations of the proboscis and how it is linked to fluid uptake rates. Previous studies (Kramer et al., 2015) have indicated that this relationship can be described as an allometric growth. Allometric growth describes a disproportionate relationship between different characters, which could be structural, physiological or even behavioral. In other words, if one character increases in measurement, the other increases at a disproportionate rate. In Equation (1), proposed by Huxley, allometric growth is represented, where y and x are the measured characters and a and b are constants.

The equation is then log-transformed, leading to Equation (2), so that b and a can be easily computed and that a diverse range of body sizes can be plotted on a single graph. Once results are gathered from the measured characters, a plot with log-transformed data can be drawn where b is the slope of the line.

b is also very important because it is an indicator of the type of allometric growth there is between the characters. Three types exist: there is the positive allometric relationship, which means y grows quickly relative to x and is indicated by b > 1, another one is the isometric allometry, which is when b = 1 and describes the case when the proportional relationship between x and y is maintained as x and y grow. The last type is negative allometry, when 0 < b < 1, which indicates that y increases at a slower rate than x (Kramer et al., 2015).
In the study effectuated by Kramer et al., Vanessa cardui L. butterflies were reared on different artificial diets and examined to determine the allometric relationship between body mass, proboscis structures and fluid uptake. Log transformed data was then plotted into a graph to analyze the slope of the line and determine the type of allometry. In Figure 4, some interesting plots are shown.

Fig. 4 Log 10- Log 10 plots indicating relationships between proboscis structures (one length, the other drinking region) and the insect's body mass (in mg). The line of best fit is accompanied with lines showing the mean confidence intervals (95%) and the slope b for each equation is bolded (Kramer et al., 2015).
As it can be observed in those plots, the study concluded that all measured proboscis structures exhibited similar trends of negative allometry (when 0 < b < 1) with body mass, indicating that when body mass increases, the proboscis structure increases at a much slower rate. This can be indeed explained by the fact that proboscis length and width can greatly affect feeding strategies: if a proboscis is too large or too long, it could prevent the insect from feeding from a certain nectar source (narrow floral corollas, for example).
However, how are proboscis structures related to fluid uptake rates? The same study showed that fluid uptake rates are greatly influenced by changes in proboscis structures. From the results in Figure 5, it can be deduced that fluid uptake rate increases as proboscis length and drinking region length increase since the slopes show an isometric allometry. With the body mass, however, the allometry is negative meaning that the fluid uptake rate decreases with increasing body mass.

Fig. 5 Table showing results from linear regression analysis to determine allometry between proboscis characters (lengths and widths measured in μm) and fluid uptake rate (mg/min) (corresponds to y). The slope values are shown in bold (Kramer et al., 2015).
Knowing the relationship between those characters can be extremely helpful since it can be used to predict a certain behavior or certain results. Since there is an allometric relationship, the proboscis functionality to feed is affected by changes in structural conformations which can be used to predict the rate of fluid uptake. This could have a great impact in biomimetic devices and research.
Moreover, the impact of changes in proboscis structures can also be analyzed in other variables. An example is the way proboscis length, body size and foraging distance are linked by an allometric relationship. This knowledge could be incredibly useful when applied to bees for example. Indeed, they play a key role in many ecosystems by pollinating flowers and crops, thus promoting gene flow among plant populations. In this domain, foraging distance information is critical for understanding how bee populations respond to landscape, and what are their pollination strategies (Greenleaf et al., 2007).
Nonetheless, the mechanisms that underlie those types of relationship remain uncertain : what developmental mechanisms ensure that some trait responds isometrically or allometrically to changes in body size or another trait? The next challenge in the study of allometry is to understand the underlying process that creates those links between certain traits.
The Fibonacci sequence
Known as “Nature's Secret Code”, the Fibonacci Sequence is a sequence of digits in mathematics where each term is the sum of the two that precede it, starting at 0 and 1, or 1 and 1; it has a second-order recurrence relationship because each term depends on the previous two and it can be represented by the following equation:
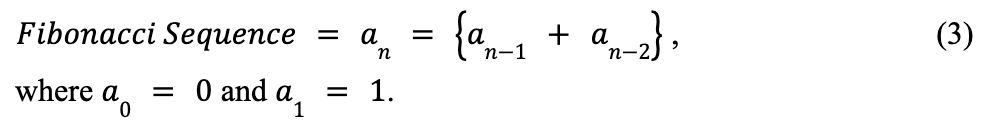
The discovery of the sequence has been accredited to Leonardo Fibonacci, whose real name is Leonardo of Pisa, due to his published tome titled “Liber Abaci” in which he explains the sequence by referring to rabbits. Fibonacci posed the Rabbit Island theoretical problem: if a pair of rabbits mate and have a litter of rabbits, how many rabbits will they produce after a year, assuming each litter contains another pair of rabbits that can mate (Fig. 6). The answer turns out to be 144, a value obtained by what is now known as the Fibonacci Sequence formula (Ghost, 2022).
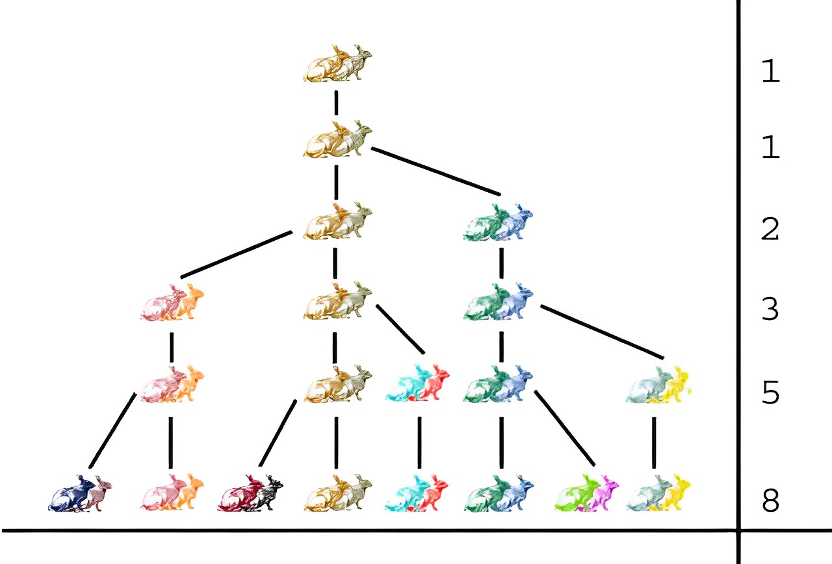
Fig. 6 Diagram of Leonardo Fibonacci's Rabbit Island Theoretical problem. Each pair of rabbits mates to produce another pair of mating rabbits. Note that the diagram only shows the first 6 terms of the sequence starting at 1 and 1 (Lewis, 2015).
The Fibonacci sequence can be observed in many different aspects of nature, such as population growth or geometry in plants; plants that need to capture a lot of sunlight arrange their leaves by following the Fibonacci sequence. However, what makes the Fibonacci sequence so interesting is its link to the famous Golden Ratio. If squares of consecutive Fibonacci widths are drawn one next to another, a spiral known as the Golden Spiral is obtained (Fig. 7). The name of this spiral comes from what's known as the Golden ratio, which is an irrational number for which the ratio of two consecutive Fibonacci values approaches.
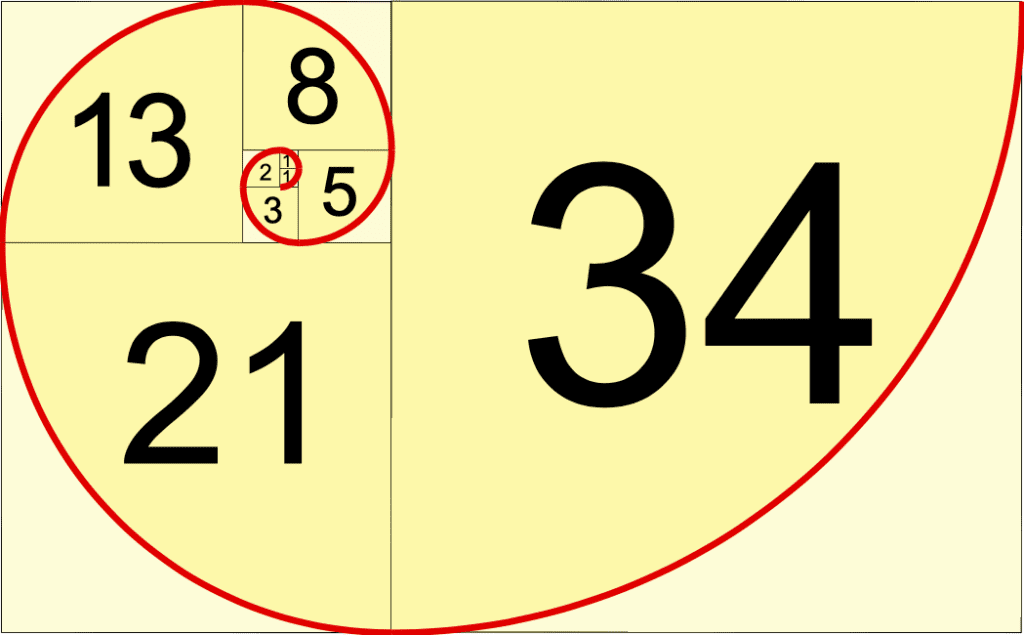
Fig. 7 The Golden Spiral obtained by tracing arcs along the consecutive squares of Fibonacci width (Fibonacci Sequence, n.d.).
Mathematical spirals
In mathematics, a spiral is a plane curve that revolves around a singular point while going further and further away from said point. There exist many different types of spirals, such as the double helix of DNA. However, the focus of this section will be on the two dimensional logarithmic and golden spirals. The logarithmic spiral (Fig. 8) is a spiral in which the radius and the angle have a logarithmic relationship; the radius grows exponentially with the angle.
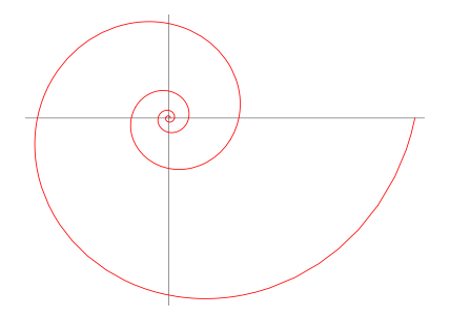
Fig. 8 The logarithmic spiral (Weisstein, n.d.).
The spiral has the following polar equation:

where r is the distance from the origin, e is the base of the natural logarithm, is the angle in degrees from the positive x-axis, and a and b are arbitrary constants.
The logarithmic spiral can be constructed by starting at a point on a series of equally spaced rays, and tracing a line perpendicular to each adjacent ray. Suppose the limit is taken as the number of rays approaches infinity. In that case, this generates a smooth logarithmic spiral (Fig. 9).
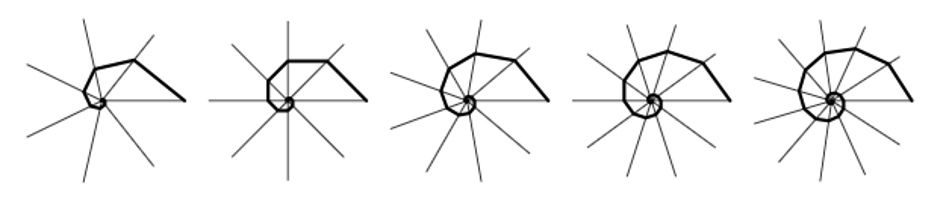
Fig. 9 The construction of a logarithmic spiral: perpendicular lines are traced on each adjacent ray starting at 7 rays, and going up to 11; as the number of rays is increased to infinity, the segments will smooth out to form the spiral (Weisstein, n.d.).
If the arbitrary constant b is taken to be

where phi is the golden ratio,
then the golden spiral is created. The golden spiral constructed from squares of Fibonacci widths is a combination of curved arcs drawn inside each square and cannot be considered a mathematical spiral. This is because the addition of curved arcs means the curvature jumps at each transition, creating something that looks like a spiral when zoomed out. Therefore, the logarithmic spiral created with the value of b from Equation (5) is the approximation of the golden spiral using a logarithmic spiral as the latter is actually a mathematical spiral related to the Fibonacci sequence and the golden ratio (Budd, 2020).
The golden ratio and its relationship to the proboscis
Represented by the Greek letter , the Golden Ratio is an irrational constant first described by mathematician Euclid. The Golden Ratio holds true for two quantities if their ratio is equal to the ratio between their sum and the larger of the two quantities. For example, it holds true for quantities A and B, where A is larger than B, if AB is equal to A + BA (Fig. 10). Specifically, the Golden Ratio begins at 1.61803 and continues forever, in a similar fashion to (Lehnert et al., 2015).

Fig. 10 A visual representation of the Golden Ratio shown in the shell of a nautilus (Lehnert et al., 2015).

Also known as the divine proportion, the Golden Ratio mysteriously occurs in countless areas of the universe — from seed pods on a pinecone to spiral galaxies such as the Milky Way. Moreover, the Golden Ratio can even be found on a microscopic level, as the DNA molecule shows numbers belonging to the Fibonacci sequence (Dvorsky, 2013).
Among insects, the proboscis of Lepidoptera (butterflies and moths) is the most prominent example of the Golden Ratio. This can be observed when the organ is in its resting position: the elastic properties of the proboscis cuticle allow it to be tightly coiled in a spiral for long periods of time (Fig. 11). Furthermore, the proboscis also fits the Golden Ratio during the coiling process (Lehnert et al., 2015).

Fig. 11 The proboscis of a butterfly in its resting position, scanning electron micrograph (The Scientist Staff, 2015).
The relationship between the Golden Ratio and the proboscis was discovered in a study using four different species of butterflies in the family Nymphalidae, where each was placed in front of a high-speed camera. The proboscis was then extended using an insect pin and left alone to recoil. Finally, specific photographs where the coils of proboscises seemed to fit the Golden Ratio were isolated and analyzed. The Golden Ratio was determined by finding the difference between the value of AB and the value of A + BA, where lower values are more desired as they are closer to fitting the Golden Ratio (Fig. 12) (Lehnert et al., 2015).

Fig. 12 Measurements used to display proboscis geometry, theta (θ) being the proboscis angle between two rays: one from the proboscis tip to the knee bend and another horizontally bisecting the coils (Lehnert et al., 2015).
Results reveal that M. cymela and L. a. astyanax are the two butterfly species with the closest fit to the Golden Ratio. Furthermore, comparison of the feeding habits among the studied species reveals that the proboscis coil of sap-feeding butterflies fit the Golden Ratio more closely than nectar-feeding butterflies (Lehnert et al., 2015).
Natural beauty and the golden ratio
The Golden Ratio or Golden Spiral is a beautiful mathematical concept which is a tricky idea to define. It is commonly said that “beauty is in the eye of the beholder” yet beauty can also be defined by thousands of ubiquitously beautiful notions. Whether there is a definition of beauty in science is a heated debate among scientists and thinkers but, the balance brought between transcendental beliefs and natural science is believed to stem back to the harmony found in the golden ratio. From being enlightening, the beauty of the golden ratio perpetuates nature with its patterns and symmetry. Just as complex as a biological system is, the golden ratio, a unique number that cannot be defined as a rational of two integers, includes a factor of √5 (Luttge, 2019). Relating beauty to irrationality makes it one of the most difficult describable notions. One example of the dualism between beauty and complex biological systems is a flower.
All plants are complex in nature as living organisms that adapt to external changes, react to pertinent factors such as nutrients, water and sunlight and have interactions with other species. Plants are an extremely diverse kingdom and one of the defining characteristics of their beauty yet complexity is phyllotaxis. Phyllotaxis is the arrangement of plant organs about an axis and can often be described as a mathematical pattern and one of the beautiful applications of the golden ratio. In many cases, phyllotaxis can be broken up into two categories, which are spiral and non-spiral leaf patterns which both sport golden attributes (Okabe, 2019). In spiral patterns, as seen in Figure 13, the leaves curve in spirals at the tip and are arranged in longitudinal rows to the stem, whereas non-spiral form vertical rows with alternating leaves. There is a pattern in both angles between rows (parastichies in spiral and orthostichies in non-spiral) which is recognized as the golden angle of 137.5° (Okabe, 2019).
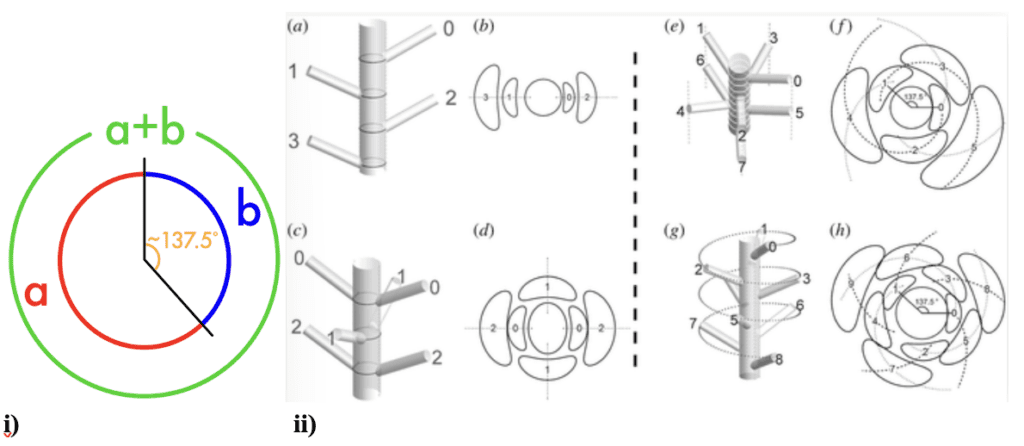
Fig. 13 i) The golden ratio transcribed into a circle. The Golden angle is represented by the angle between golden sections a and b. ii) Non-spiral phyllotaxis side view shown in (a) and (c) and then top view in (b) and (d). Spiral phyllotaxis shown in (e), (f), (g) and (h).
This fractional angle of divergence describes how the leaves around the central axis are and gives rise to the idea of beauty in a flower. This arrangement results from optimal anatomical structure because of the molecular dynamics with surrounding ecosystems. The Fibonacci sequence is intrinsically related to the golden ratio and similarly governs phyllotaxis, it is thus presumed to contribute to the beauty in a flower. Values of the patterns in nascent leaves follow a rational Fibonacci sequence, the most commonly ⅖ having 5 leaves rotating every 2 turns (Okabe, 2019). However, the sequence follows a pattern derived from the Fibonacci sequence: fn = 1, 1, 2, 3, 5, 8, … Namely this rational sequence looks like
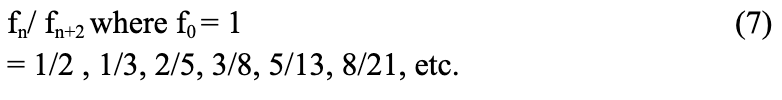
The presumable inclinations towards this particular phyllotaxis pattern are directed at efficiency in evolution. Plants with many remarkable different lineages and mechanisms have been noticed to have similar organ arrangement patterns. Though very distant in the plant kingdom, Moss and seed plants find the causal link of phyllotaxis in development. In juvenile phases, a seed plant branches according to the Fibonacci sequence and spiral mosses will have spirals emerging at Fibonnaci rational number of turns (Okabe, 2019). This rationalizes the idea of adaptive phyllotaxis to golden ratio related patterns which optimizes the robustness and energy efficiency particularly with light absorption of the biological system.
Further in plants is the arrangement of seeds at centers of flowers. The seeds arrange themselves in spirals and propagate out of the center spiral at angles of the golden angle (Thapa, 2018). This golden ratio allows them to fill the entire space without gaps and is what provides the appearance of wholeness and conformity to beauty. This can be seen easily in the seeds of a pinecone or sunflower, as seen in Figure 14.

Fig. 14 (a) Spiral pattern apparent in pinecones (b) spiral pattern apparent in sunflower seeds (Thapa, 2018).
Molecular patterns of the golden ratio
From natural occurrences arises the question of molecular governance of the golden ratio. Ionic interactions are one of the fundamental chemical interactions in life and understanding their conditions is vital to characterize them. One formal definition of mathematical beauty is on the basis of fitness. Recurring proportion arrangement in objects tends to make them more appealing, it is defined as “if beautiful is conceived as a conformity of the parts to one another and to the whole, and if […] all understand is first made possible by the means of formal connection, the experience of the beautiful becomes virtually identical with the experience of connections” (Heisenberg, 2001). This concept of connection and fitness brings us to the intrinsic properties of beauty, which would be the molecular makeup that defines its conformity. Should the parts (molecules) of the whole (object) fit together as a means of connection that is conceived beautifully, then beauty is experienced. Hence chemical architecture is an inherent characteristic of beauty, and its golden ratio rationalized structure.
Ionic radii between molecules in many dissolved ionic crystals have been related to the golden ratio by the golden sections d(MM)/Φ2 and d(XX)/Φ in metal (M) and halogen (X) solutions (Sener, 2009). The ionic-water distance is found to increase with a proportionality constant that is, moreover, a function of Φ the golden ratio (Sener, 2009). Dissolved states of electrolytes, especially in water, the most common solvent in nature is of great interest, particularly considering acids and bases. The partial dissociation of electrolytes can be explored using the study of the ionic radii of aqueous compounds and the radius of hydration bonds. This is particularly fascinating with cationic (dA+) versus anionic radii (dA-). In Fig. 15, it is assumed that for any AB, which is the molecular distance d(AA), its length can be divided into golden sections (Ap and PB), which give the cationic and anionic radius (Sener, 2009).

Fig. 15 The Golden point (P) on a line (AB). For any atom A, if AB = 2BC = d(AA), then AP = d(A – ) and BP = d(A + ) are the Golden sections denoting the anionic and cationic radii of A (Sener, 2009).
Golden ratio in biomimicry
Molecular architecture naturally expresses the golden ratio. However, humans have taken inspiration from this natural concept in art and technology. Mathematics has inspired art and culture for centuries and as one of the fundamental aesthetic mathematical governing laws, the golden ratio tends to be a driving factor of proportions. One of the most common uses of its spirals and sections is in architecture, bringing balance and proportionality to construction works. Some of the most well known and first believed applications are to the Great Pyramids of Giza and the Parthenon (Thapa, 2018). Whether these are actually true applications is still a source of debate but their very slim margin errors solidify this belief. Many believe that mathematicians and others are simply hunting for examples of this proportion and that it was in fact not a consideration in these objects. The Parthenon and Taj Mahal seem to have an outstanding number of components that fit into golden rectangles as seen in Figure 16, and spirals including the ground plan and floor plan layout and the harmonic relationships of the facades giving a semblance of order to the system (Thapa, 2018).

Fig. 16 Golden rectangles found in iconic architectural structures: The Parthenon in Athens, Greece, and the Taj Mahal in Agra, India.
These ancient techniques inspire technology to grow in inspiration of the mystifying golden ratio. Modern architecture continues to use these proportions to please human senses, while graphic design and beauty standards conform to the geometry derived from the golden ratio. However, it is more than simply the aesthetic beauty of the golden ratio that makes it permeate so many natural mechanisms. Its underlying keys to efficiency and optimization allow it to produce a guideline for engineering. One approach that parallels the golden ratio related arrangement of plant organs is the enhancement of solar panels. A recent study in 2017 by Ygo and Maisog at the Central University of Mindanao in the Philippines found a staggering 26.13% increase of power output with a solar tree in the shape of a golden spiral (Benguar, 2019), though this does not elicit causation of the golden spiral producing more efficient systems. Although many may not agree with the link between spirituality and science that the golden ratio draws, the aesthetically pleasing balance that it brings gives inspiration to the modern world.
Conclusion
The proboscis is no doubt an important organ studied with various approaches. This paper explored, in particular, the allometry and golden ratio relationships seen in the butterfly proboscis. Allometry refers to the relationship between the different components of a structure and how they interact or affect certain functions. Since the proboscis is used for feeding in butterflies, the fluid uptake rate is certainly affected by structural aspects of the proboscis such as its length. The structure of the butterfly proboscis, its coiled up spiral shape in particular, also exhibits a relationship with the Golden Ratio and the Fibonacci sequence. It is not uncommon to see this intriguing irrational number in nature as many natural phenomena, such as the seeds in sunflowers or the shell of the nautilus, display the Golden Ratio in their geometry. The Golden Ratio is not only a topic of interest in mathematics or biology, but it also has many applications in architecture and art because of its aesthetically pleasing proportions and harmony; it brings beauty and balance to modern works. Additionally, the Golden Ratio and Fibonacci sequence are emerging topics in engineering due to their applications in stress analysis, and efficiency in structural elements.
References
Benguar, A.N.D., Casiano, P.G.T., Valdehuza, T.L., & Tan, D.A. (2019). Golden Ratio Applied in the Orientation of Solar Cells in a Golden Spiral Solar Panel. International Journal of Development Research, 8(5), 20416-20420.
Budd, C. (2020, February 23). Myths of Maths: The golden ratio. PLUS. https://plus.maths.org/content/myths-maths-golden-ratio
Dvorsky, G. (2013). 14 interesting examples of the golden ratio in nature. Mathnasium. https://www.mathnasium.com/blog/14-interesting-examples-of-the-golden-ratio-in-nature#:~:text=It's%20call%20the%20logarithmic%20spiral,shape%20of%20certain%20spider's%20webs.
Fibonacci Sequence. (n.d.). Mathisfun. https://www.mathsisfun.com/numbers/fibonacci-sequence.html
Ghose, T. (2022, January 03). What is the Fibonacci Sequence? LIVESCIENCE. https://www.livescience.com/37470-fibonacci-sequence.html
Greenleaf, S. S., Williams, N. M., Winfree, R., & Kremen, C. (2007). Bee foraging ranges and their relationship to body size. Oecologia, 153(3), 589–596. https://doi.org/10.1007/s00442-007-0752-9
Heisenberg, W. (2001). Science and the beautiful. In K. Wilber (Ed.), Quantum questions (pp. 56–69). Boston: Shambhala.
Kramer, V. R., Mulvane, C. P., Brothers A. (2015). Allometry among Structures of Proboscises of Vanessa cardui L. (Nymphalidae) and Its Relationship to Fluid Uptake. The Journal of the Lepidopterists' Society, 69(3), 183-191 https://doi-org.proxy3.library.mcgill.ca/10.18473/lepi.69i3.a5
Lehnert M. S., Monaenkova D., Andrukh T., Beard C. E., Adler P. H., Kornev K. G.
(2013). Hydrophobic–hydrophilic dichotomy of the butterfly proboscis. J. R. Soc. Interface.102013033620130336 http://doi.org/10.1098/rsif.2013.0336
Lehnert, M. S., Brown, E., Lehnert, M. P., Gerard, P. D., Yan, H., & Kim, C. (2015). The golden ratio reveals geometric differences in proboscis coiling among butterflies of different feeding habits. American Entomologist, 61(1), 18-26. https://doi.org/10.1093/ae/tmv005
Lewis, H. (2015, March 21). The Mathematics of Rabbit Island. Maths careers. https://www.mathscareers.org.uk/the-mathematics-of-rabbit-island/
Luttge, U., & Souza, G.M. (2019). The Golden Section and beauty in nature: The perfection of symmetry and the charm of asymmetry. Progress in Biophysics and Molecular Biology, 146, 98-103. https://doi.org/10.1016/j.pbiomolbio.2018.12.008
Okabe, T., Ishida, A., & Yoshimura, J. (2019). The unified rule of phyllotaxis explaining both spiral and non-spiral arrangements. Journal of The Royal Society Interface, 16(151),
Pometto, Suellen Floyd. (2019). Self-Repair and Self-Cleaning of the Lepidopteran Proboscis. All Dissertations. 2452. https://tigerprints.clemson.edu/all_dissertations/2452
Sener, B. (2009). Innovations in Chemical Biology. Springer Science + Business B.V.
Thapa, B.G., Thapa, R. (2018). The Relation of Golden Ratio, Mathematics and Aesthetics. Journal of the Institute of Engineering, 14(1), 188-199. https://doi.org/10.3126/jie.v14i1.20084
The Scientist Staff. (2015. Image of the Day: Golden Ratio [Photograph]. The Scientist. https://www.the-scientist.com/image-of-the-day/image-of-the-day-golden-ratio-35800
Weisstein, E. W. (n.d.). Logarithmic Spiral. Wolframalpha. https://mathworld.wolfram.com/LogarithmicSpiral.html
Zeng, L., & Wang, G. (2009). Modeling golden section in plants. Progress in Natural Science, 19(2), 255-260. https://doi.org/10.1016/j.pnsc.2008.07.004