Closed Kinematic Chains: A New Perspective and Analysis of Biological Ability

Andrea Khoury, Nikki Lal, Spencer Levine, Laura Camila Penuela Cardenas

Abstract

Kinematic chains are wonderful phenomena that appear in biological organisms. They involve looped segments connected by joints and these loops are either open or closed. In a closed system, movement from any particular joint will generate movement at all other joints in a specific manner, as these joints cannot move freely. The method in which joints are linked and their freedom/inhibition of movement can produce a wide range of results desired by an organism or engineering design. This versatility and precision make these chains very good candidates for mechanical systems and make them more able than classical physics to analyze biological systems. This paper explores the concept of kinematic chains through analysis of examples where Newtonian physics fails to provide an answer, as well as the exploration of their utility in the species Odontodactylus scyllarus (Peacock Mantis Shrimp) and Mystrium camillae (Dracula ants) and, finally, their application in engineering design.

Introduction

The principles of closed kinematic chains, further referred to as CKCs, and even kinematic chains in general, is a relatively new concept. The first known hypothesis of their existence comes from a late 19^th century mechanical engineer, Franz Rouleaux. For reference, the developments of calculus and Newtonian physics, which are still very prominent today, took place in the 17^th century! Rouleaux “proposed that rigid, overlapping segments were connected via joints and this created a system whereby movement at one joint produced or affected movement at another joint in the kinetic link” (“Kinetic Chain” | Physiopedia, n.d.). These systems can be either considered open or closed or they can be a mix of both mechanisms (Fig. 1).

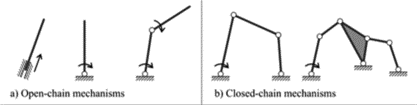
As we can see, open chains have loose ends that will not move in a predictable manner and thus will be difficult to control and not very useful for biological organisms, which desire maximum efficiency and utility. On the other hand, closed chains have fixed joints on all edges. The resulting motion of this system is much easier to work with and is in fact very versatile.

Based on what has been presented so far, we get the impression that closed kinematic chains lose their efficacy as more free, open links are added. First, this observation is correct. As discussed further in the next section, smaller chains such as the three-joint triangle and four-joint quadrilateral are the most useful for biological organisms and engineers due to their stability and predictable movement. There is one further concept which is very important in biological CKCs and should not be overlooked in engineering designs: heterarchy. As opposed to a normal hierarchical system where there are numerous bottom elements that are organized below fewer, and larger structures which are often more powerful, CKCs in biology can flip the hierarchy at any given point to achieve a desired result. To make this a little clearer, let us consider the example of an elephant's trunk. As we have previously discussed in our first instalment, elephants' trunks have the ability to control the amount of force they exert when picking up an object. From the perspective of CKCs, this can be explained by the anchoring and stabilization of different muscle groups. These controllable modifications give elephants the ability to pick up a peanut or even uproot a tree!

As you may have guessed, CKCs are ubiquitous in all large, multicellular organisms with joints. Mastering their fundamentals and using the principles that nature has developed over millions of generations will allow engineers to harness their utility and create more powerful, innovative projects.

To begin our journey, we clarify the cruciality of this study. Then, we will see how the species Odontodactylus scyllarus (Peacock Mantis Shrimp) and Mystrium camillae (Dracula ants) utilize these systems. Finally, we see some engineering projects involving CKCs and contrast the principles of CKCs to Newtonian Physics. Let us delve right in.

Why Are We Talking about the CKCs

The Shortfalls of Lever Mechanics: The Iron Cross

The Iron-Cross exercise is an impressive position that gymnasts hold for over 2 seconds. It is characterised by maintaining 90º shoulder abduction in the frontal plane with both limbs, while the elbows are extended. The cross demands that the gymnast holds their shoulder in an anatomical position that involves the extension of passive structures of the glenohumeral joint, causing shoulder instability (Carrara et al., 2016) (Fig. 2).

If we consider the fundamentals of Newton's second law, we observe something shocking: this position is physically impossible to hold! Assuming the body of the gymnast is a heavy box hung from a rope that has horizontal attachment points, the mass of the rope can be viewed as negligeable compared to the mass of the box (Fig. 3).

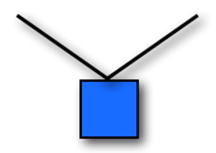
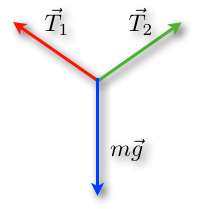
Since the box, and hence the gymnast's body, is in equilibrium, according to Newton's second law, the different forces should add up (Rhett, 2008). Since the acceleration is zero for an object in equilibrium, all the acceleration components are also zero. In two dimensions, this means that a_x = 0 m/s² and a_y = 0 m/s². Substituting these values into the second law (ΣF_x = ma_x and ΣF_y = ma_y) shows that the x component and the y component of the net force must each be zero. In other words, the forces acting on an object in equilibrium must balance (“Equilibrium applications of Newton's laws of motion” | WebAssign, 2010).

In fact, an object can be acted upon by several forces at the same time. We know that a force is a vector quantity which has a magnitude and a direction. So, if all forces acting on an object are exactly balanced, that means that no net force is acting on it (“Equilibrium of Forces” | NASA, n.d.).

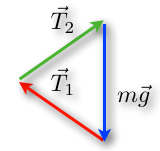
We want to increase the tensions in the rope. By performing this change, the lengths of the tension vectors will then be longer, but the length of the blue vector will not change because of the constant weight (Rhett, 2008) (Fig. 6).

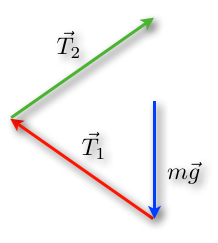
An important concept is that an object at rest will stay at rest and an object in motion will stay in motion. By changing the angles and perspectives of views, we find a triangle as well. But since ropes can only pull in the direction of the rope, this will result in another structure (Rhett, 2008). As a matter of fact, tension is a pulling force because ropes cannot push effectively (“What is tension?” | Khan Academy, n.d.) (Fig.7).

From a mathematical point of view, increasing the tension could never result in a horizontal cable. As the angle decrease, so does the value of the sine function of the angle. In fact, the forces will always contain a vertical component to compensate the weight of the object. To compensate the decreased sine value, the tension force is increased and becomes more and more unattainable as we get closer to a 90° angle (Rhett, 2008).

In the case of the iron cross exercise, having nearly horizontal arms would require very high forces involved and the arms could not physically stay parallel to the ground as the exercise proposes. However, multiple athletes were able to hold the correct position because the arm is not a single rope and there are several “attachment points” for the arm. We must look beyond simple Newtonian lever mechanics! (Rhett, 2008).

Closed Kinematic Chains

Instead of studying biological movements using the standard methods of Newtonian physics, which are sometimes insufficient, we are developing closed kinematic chains as a new way of approaching those situations. They provide a simple and efficient mechanism with multiple applications and contribute to our understanding of biological motion. In fact, kinematics focuses on the geometry of motion.

In a biological context, CKCs are modular units nested within others at multiple size scales as part of an integrated movement system that extends throughout the organism (Levin, “Tensegrity: the new biomechanics.”). Each part is structurally and functionally connected with the other parts. Furthermore, the analysis of the CKC geometries in living tissues shows that they are ubiquitous, mechanically efficient, and evolutionary-conserved structural arrangements.

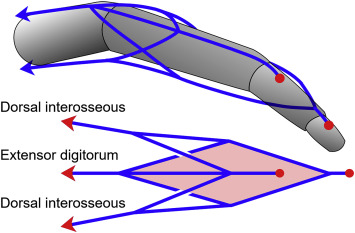
In a closed kinematic chain, forces at one point can result in the manifestation of the source in areas far removed from the point of origin. For instance, in the human anatomy, shoulder muscles take part of the fingertip strength. Moreover, one muscle can lock a chain. This leads to simple stability and efficient energy. Fingers for example can be modeled as an open chain if you look at the joints, but the tendons present make it more of a CKC.

Further, the point of application is a key element as well. As a matter of fact, when playing the piano, shoulders are immobile whereas fingers are moving. On the contrary, when climbing, fingers are balanced to provide stability to the climber while shoulders are in motion. An important property is that the increase of links in chains makes them less stable. For instance, the 3-bar shapes – triangles – are great options because of their inherent stability. Nevertheless, the planar four-bar linkage is the simplest movable closed-chain linkage. It consists of four bodies connected in a loop by four joints. They are generally configured so the links move in parallel planes. Thus, geometric arrangements with 5 or more bars are uncontrollable on their own.  

Looking back at the iron-cross example, although the position is mathematically impossible to perform from a Newtonian perspective, Closed Kinematic Chains offer a new way to explain the exercise. As a matter of fact, no natural laws are transgressed nor broken but the reasons are yet to be stated. Bioengineers believe there are links between muscles in the neck to the shoulders, shoulders to the ribs and going all the way to the spine. This would be represented with triangle series, already presented as three-bar shape chains.

Moreover, according to experts, Closed Kinematic Chains adduction occurs with the position. The hands are fixed on the rings, and the shoulder adductors are used concentrically to raise the body as the arms are pulled down toward the sides from the position. Gymnasts can avoid excessive elevation of the shoulders by contracting muscles that tend to depress the humerus and scapula two bones of the human upper limbs (Clippinger, 2016).

Another factor to consider is that, during the iron cross, muscles in the biceps, brachii and middle deltoid stabilize the glenohumeral joint superiorly, and the muscle triceps brachii prevents upward dislocation of the humeral head and keeps the elbow joint into extension. Thus, the shoulder muscles activity is adaptable and created in relation to the stress induced by each device on the shoulder joint for the same movement (Bernasconi et al., 2006). The exercise is not impossible after all!

Biological Examples

Odontodactylus scyllarus – Peacock Mantis Shrimp

 The peacock mantis shrimp (here abbreviated as P.M. shrimp) or Stomatopoda, Odontodactylus scyllarus is a crustacean that can notably be found on the shallow parts of the Indian and Pacific Oceans (“Peacock Mantis Shrimp” | Oceana, n.d.) (Fig. 12).

For many years, these animals have been studied for their astonishing forelimbs which are also referred to as raptorial appendages (“raps”). As a matter of fact, the latter serve them as both a feeding and a defense mechanism for they use the strength of their ‘punch' to break open shells and dismember other crustaceans, amongst other.

P.M. shrimp can be divided into two categories according to the characteristics of their raptorial appendages. They can either be ‘spearers' or ‘smashers'. The former have “sharp barbs on their raps used to impale fish, shrimp, or other soft-bodied prey” (Fig. 13) whereas the latter have “an inflated, calcified “heel” on their raptorial appendage” (“How smashing!” | UCMP Berkley, n.d.) (Fig. 14). Here, we will primarily focus on examining smashers' raps, however. 

To begin, it is essential to take a close look at specific parts of the morphology of the raptorial appendage of smashers.

In a study carried out by Patek et al., the researchers found concrete proof that demonstrates the theory that a four-bar linkage system is at the core of the proper functioning of smashers' raps (Patek et al., “Linkage mechanics and power amplification of the mantis shrimp's strike”). This system forms a closed kinematic chain (CKC) which is what is thought to control the “click” mechanism that lets energy be stored as the extensor muscle in the rap contracts. Moreover, P.M. shrimp have two sclerites (or ‘latches') that stop the extensor from extending the limb and, when the ‘latches' are released, they allow limb extension. The CKC and the two sclerites thus contribute a great deal to the power amplification system, which will be discussed in greater detail later on (refer to Patek, 2007 in Appendix).

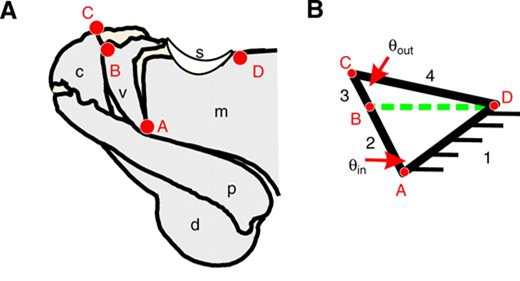
In the figure above, the length of the four links and the input angle were used to calculate the length of the diagonal (L_db):

L_{db}=\sqrt{L_2^2+L_1^2-2L_1 L_2 cos⁡(θ_{input})}

(1)

which, in turn, permitted the calculation of the output angle:

θ_{output}=arccos⁡[{L_3^2+L_4^2-L_{db}^2 \over 2L_3 L_4}]

(2)

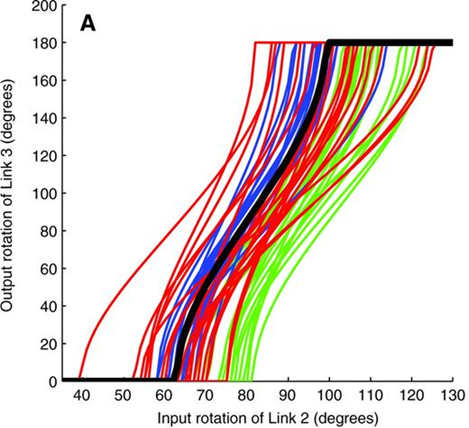
With the help of these measurements, it became then possible to determine the range used by smashers between which the input linkage remains functional. Hence, it was noticed that P.M. shrimp's linkage mechanism is operational between 40° and 120° (Patek et al., “Linkage mechanics and power amplification of the mantis shrimp's strike”) (Fig. 16).

What is more, another key part of the morphology of smashers' raptorial appendages that needs to be examined is the saddle. In mathematics, this kind of structure is known as a hyperbolic-paraboloid or anticlastic surface. It is characterized by being a double-ruled surface that “has a convex form along one axis, and a concave form on along the other” (“Hyperbolic paraboloid in construction” | Designing Buildings Wiki, 2020). These properties respectively allow the surface to be constructed with only straight lines and make it a strong in compression, thus permitting the forces to be spread over the entire surface (Concrete Construction Staff, 1959).

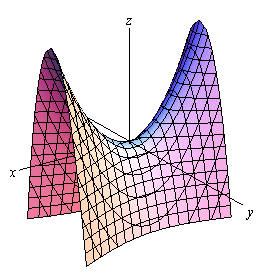
Looking at the saddle of P.M. shrimp from a biological perspective, it becomes evident that this structure is very beneficial for it can be made with few and ‘cheap' components, and it also acts like a spring which makes it offer great stability when tension or compression are exerted upon it (Fig. 18).

The final part of the anatomy of smashers' raps that must be mentioned is the distal portion of the raptorial appendages which is composed of the dactyl ‘heel' and the propodus (Fig. 18). 

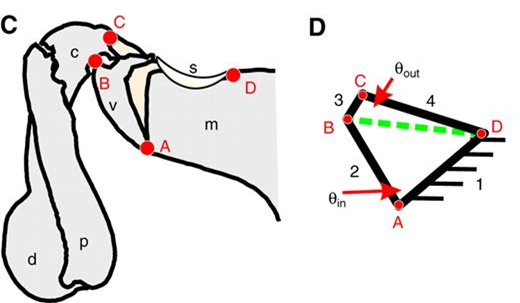
On another note, we will now discuss the details of how P.M. shrimp are capable of breaking mollusk shells. Smashing the latter requires a lot of strength and it is evident that smashers' muscles by themselves cannot provide the required force to break open the shells. Hence, they need to have a way of amplifying the force they can produce to accomplish this action. This is when their power amplification system comes in handy.

When P.M. shrimp need to perform a potent strike, they contract, in a simultaneous manner, their extensor and flexor muscles. Once the limb is contracted, the ‘spring' is in compression and it is therefore storing elastic potential energy. At the moment in which the flexor relaxes, the sclerites release, the saddle converts the potential energy it stored into kinetic energy and the extensor can then make the limb extend. The dactyl ‘heel' and the propodus are thus ‘pushed' and the former hits the shell (Patek, 2015).

What are probably the most captivating remarks about the strike are its duration, speed, and strength. As a matter of fact, the entire hit has been observed to last only a couple of milliseconds and reach speeds under water in the range of 10-24 m/s (Burrows, 1969; Burrows and Hoyle, 1972; Patek et al., “Biomechanics: Deadly strike mechanism of a mantis shrimp”). Hence, smashers detain the Guinness World Record for “strongest self-powered strike by an animal”! (Dimery, 2019). In addition, P.M. shrimp may deliver forces surpassing 1 000 N, which is hundreds of times greater than their body weight (Patek et al., “Linkage mechanics and power amplification of the mantis shrimp's strike”).

Furthermore, a fascinating phenomenon that occurs right when the ‘heel' hits the shell is the formation of what is known as cavitation bubbles. Essentially, the incredibly high speed at which the limb strikes causes a rapid pressure drop which makes the water between the dactyl ‘heel' and the shell vaporize, therefore resulting in cavitation bubbles being formed. When the bubbles collapse, “there is a small implosion in the water, which produces heat, light, and sound” (Patek, 2015) (Fig. 19). 

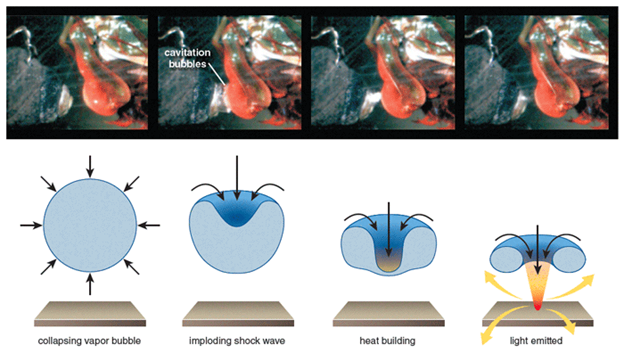
From experiments carried out by Patek et al., two pronounced force peaks distanced by half a millisecond were recorded by a load cell measuring the force of the P.M. shrimp strike. Evidently, the first peak was caused by the limb hitting the cell. However, the second peak was harder to explain. Later, it was concluded that this other peak was due to the pressure waves resulting from the collapse of the cavitation bubble (refer to Patek, 2007 in Appendix). This means that smashers ‘exploit' cavitation to their advantage.   

It is expected that the dactyl ‘heel' gets worn down from its constant use. Nevertheless, this is not an issue for P.M. shrimp because they molt approximately every three months and so they regenerate their limbs every time (refer to Patek, 2007 in Appendix).

Mystrium Camillae – Dracula Ants

Mystrium camillae, more commonly referred to as Dracula ants, get their particular name from the fact that they chew holes on their larvae and feed on their blood. These animals can be found in the tropics of Africa, Asia, and Australia (Katz, 2018) (Fig. 20).

Similarly to P.M. shrimp, Dracula ants have a ‘spring-latch' mechanism that is ‘managed' by a CKC and that permits them to amplify the power produced by their jaw muscles. Nonetheless, unlike smashers who do not have this structure on the dactyl ‘heel', these ants have it comprised on the accelerating mandibles themselves (Larabee et al., 2018). In the case of Mystrium camillae, this is called a ‘snap-jaw' mechanism.

Moreover, an interesting peculiarity of the ‘snap-jaw' mechanism of Dracula ants is that they do not close their flattened jaws from an open position, but rather press the tips of their mandibles against each other and bow the base of their jaws inwards (Larabee et al., 2018). Doing this induces stresses that increase the elastic potential energy of the spring that is present within the jaws. When the ‘latch' releases, the stored energy is converted into kinetic energy and then the faster, ‘striking' mandible can slide over the slower, ‘loading' mandible (Larabee et al., 2018).

In a research conducted by Larabee et al., the jaw of the Dracula ant was modelled as a linear rod capable of rotation exclusively around one of its ends. Thus, its moment of inertia (I) was calculated using I=(mr²)/3, where m represents the mass of the mandible and r represents its length. Having this value, it became possible to determine the amount of kinetic energy (E_k) stored by the jaw using E_k=(Iω²)/2, where ω is the maximum angular velocity that the jaw can reach during a strike. This allowed to calculate an estimate of how much power is needed by the mandible to snap:

P={(E_k)_{max}\over t_{(E)_{max}}\sdot M_{add}}

(3)

where t_(E)max corresponds to the time at which (E_k)_max is reached, and M_add corresponds to the mass of the adductor muscle that is present in the jaw (Larabee et al., 2018).

From various analyses of “high-speed strike videos”, Larabee et al. determined that “a complete strike occurred in as little 22.9 µs and had an average duration of 50.2 µsec (s.d. ± 22.0 µs)” (Fig. 21).

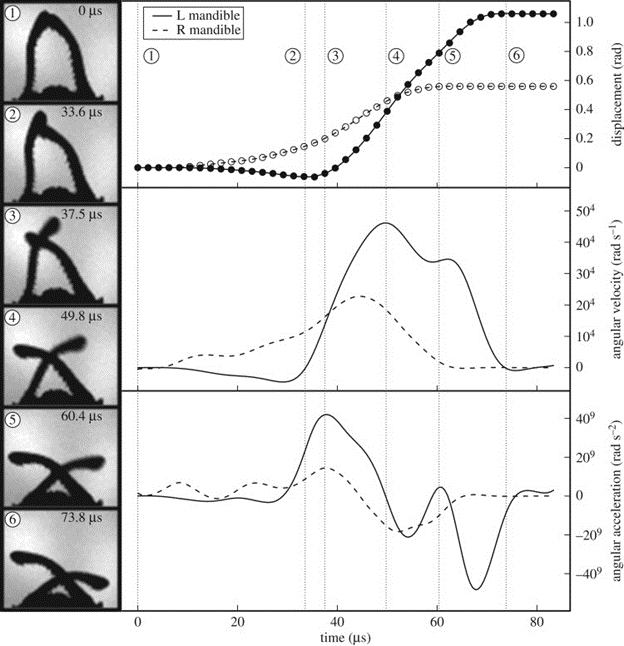
Additionally, Dracula ants' mandibles were seen to attain peak linear velocities around 90 m/s and accelerations surpassing 10⁶ × g. To try to make sense of how fast the snap is, the movement of Mystrium camillae's jaws is approximately 5 000 times faster than the blink of an eye! (Katz, 2018).

The research on Dracula ants is far from being finished as there remain quite a lot of unknown details regarding this ‘snap-jaw' movement. For instance, the force produced by the mandible has yet to be measured and a more in-depth analysis of the morphology of the jaws is required to have a better understanding of the power amplification system used by Mystrium camillae.

Engineering Examples

CKC Machines

As presented earlier, closed kinematic chains are a useful when observing biological motion that we have yet to mathematically comprehend. In engineering, there are many more applications of CKC mechanics. Robots with CKCs are bodies created with members and joints, like regular Newtonian machines. They have a certain topology that describes the interconnections of all the links and actuators that somewhat control their joints. The degree of freedom of these systems, which differ with complexity, is the ability for the system to change its configuration in a set number of directions. With fixed topology, the number of actuators does not exceed the degree of freedom (Nahon and Angeles, 1989).

As an example, look at the Gough-Stewart platform, a robot with CKCs, six degrees of freedom, and six legs, each actuated by prismatic spherical and universal joints, seen in Fig. 22. One application of this system is aircraft simulations; the degrees of freedom allow for movement that can simulate air travel (“Modern Robotics, Chapter 7: Kinematics of Closed Chains” | Northwestern Robotics | YouTube, 2017; Wang et al., 2002).

This platform is a parallel robot, meaning the robot's actuated legs connect a rigid, constricted base to a moving platform. Parallel robots are distinct from open-chain robots because they are generally stronger, since their forces are distributed over multiple legs, and the calculations of inverse kinematic equations is easier for parallel robots, whereas forward kinematic equations are simpler for open-chain robots (“Modern Robotics, Chapter 7: Kinematics of Closed Chains” | Northwestern Robotics | YouTube, 2017).

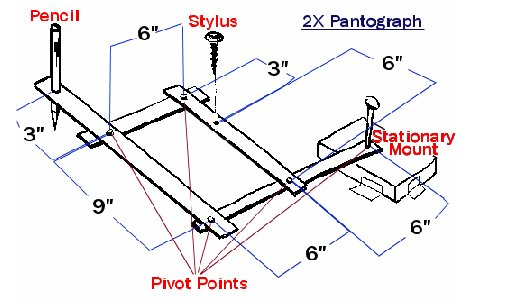
Another example of CKC systems is the Strandbeest. Since 1990, Theo Jansen has been working and developing his various models of his Strandbeest: a “beach animal” made entirely of PVC pipes that can stroll along the beaches of the Netherlands (Jansen, 2020; “Strandbeest Multi Tripodes” | Theo Jansen | YouTube, 2020).

This “animal” is wind powered and walks because of CKC principles. As described in one of Jansen's videos explaining his creations, the Strandbeest consists of multiple legs connected to a backbone, in the shape of CKCs, with sails to allow for movement (Jansen, 2020). The backbone links directly affect the motion of the feet. They move in circular patterns similar to a pantograph, which is the simplest CKC system that stays fixed at one point and draws at another point because of circular patterns in its links (Editors of Encyclopedia Britannica, “Pantograph”). The length of the links of the Strandbeest backbone is particular, as the length determines the curves produced by the circular movements. Jansen created a computer program to help him with the trial-and-error process of determining proper lengths for his Strandbeest (Jansen, 2020). The computer program generated curves corresponding to particular length proportions. In the 1990s, Jansen finished his first models of the Strandbeest, complete with shoes designed for walking on the sandy beaches of the Netherlands (Jansen, 2020).

Contrasting Principles of Newtonian Physics and CKCs

Newtonian Physics has greatly impacted our understanding and applications of physics, but modern researchers are continuing to learn that these principles break down for biological systems. With linear physics, lifting a 100 kg weight should crush a weightlifter's spinal vertebrae. As well, the pressure buildup of blood vessels in the brain from a single heartbeat should cause the skull to explode (Levin, “Closed kinematic chain mechanisms”). In the example of the iron-cross exercise, Newton's Second Law does not hold true for the system, as the gymnast may hold their weight with horizontal arms. This is because the muscular system of biological organisms is much more complicated than tension in single ropes.

Newtonian physics principles are the basis of most physics principles, and have many advantages for engineering systems, such as statics. In statics, Newton's Laws are the solution technique used for problems like trusses and other geometric structures. Newton's Second Law, F = ma, is applied in vector and scalar notations, as well as extended to rotations, where the force at static equilibrium of a system is 0:

ΣF_x = 0       ΣF_y = 0       ΣF_z = 0              ΣM_x = 0       ΣM_y = 0       ΣM_z = 0

In these equations, F is the force in the 3-dimensional directions of x, y, and z, and M is the torque, or moment, in 3D space as well (Roylance, 2000). Geometric structures and static structures are popular applications of these principles because the forces and moments are linear in fashion.

For biological systems, the principles emerging behind CKCs are different and more effective in describing the non-linear forces in organisms. Biological systems are simply built on different principles than engineered structures. For a given building, the foundation of that building must be the strongest part, as is built up with rigid materials to attenuate the effects of external forces on its stability (Levin, “Closed kinematic chain mechanisms”). Closed kinematic chains have been seen in engineering for quite a while but are only beginning to be applied for biological analysis. Previously, lever mechanics were used and the discrepancies were ignored (Levin et al., 2017). CKC models and kinematics focus around mechanical loops and not linear systems. They can be applied to muscular links, coupled tissues, and tendons, as seen in the biological examples of the P.M. shrimp and the Dracula ant (Levin et al., 2017). Two important characteristics of CKC models are the axial stiffness of the links connecting each joint and the closed-chain configuration that creates the dynamic stability in the system. The CKC system of coupled tissues in organisms, like fish, enable certain structures to move at great speeds even without the presence of muscle tissue. This allows the organisms to capture their prey efficiently. In tetrapods, the stiff ligamentous links in the knee allow for support during the motion of limbs (Levin et al., 2017). This is why, for the iron-cross example, a position that is “physically impossible” can be achieved; shifting perspectives from linear mechanics to CKC mechanics, such a state of an organism can be properly analyzed and understood as the cause of closed-chains in the musculoskeletal system. As we continue to approach biological systems with the lens of CKC mechanics, we will develop the analysis of our own bodies and the organisms around us like we developed the analysis of static structures with Newtonian mechanics.

Conclusion

In conclusion, the kinematics of biological systems seems to be better analyzed using closed-chain models of kinematics than classical physics. The iron-cross exercise is an example of a classically impossible, yet biologically possible, pose that, when properly analyzed by considering biological systems as closed-chain systems, mathematically makes sense as well.

The first examples were biological organisms – the peacock mantis shrimp and the Dracula ants – that use CKCs to accomplish otherwise impossible tasks. The organisms both have CKCs that control ‘spring-latch' mechanisms that may greatly amplify the power in their appendages or mandibles, respectively. Through the scope of Newtonian physics, the muscles present in these systems would never be able to produce the power amplification seen in these organisms, but when CKC principles are applied to the mechanism, we may analyze the system more accurately and the results match the phenomena.

The principles behind CKC mechanisms are already established in engineering applications, for example, the Gough-Stewart platform and the Strandbeest. The Gough-Stewart platform is a six degree of freedom, closed-chain robot that distributes its weight over 6 actuated legs, whereas the Strandbeest is a giant plastic machine that uses closed-chain mechanisms to walk itself along sandy surfaces. Both designs were initially based off CKC mechanisms to be able to accomplish their tasks, in contrast to biological systems, which have hardly been analyzed with the lens of CKC mechanisms.

The advantages of Newtonian physics are definitely ample when looking at static systems, for example, but we are slowly seeing that modelling biological systems with Newtonian physics makes us ignore too much. CKC models are much more suitable for the analysis of biological systems, as Newtonian physics are unable to support the phenomena we see. It all comes down to perspective because we, as engineers and researchers, must be able to fit a phenomenon to an appropriate model and recognize when our methods are unfit. As we continue to learn about biological systems, it is fascinating to recall how biology holds answers that our mathematics and physics understandings are not able to find. At least, not yet.

Appendix

“Modern Robotics, Chapter 7: Kinematics of Closed Chains.”, 27 August 2017, Northwestern Robotics, YouTube, https://www.youtube.com/watch?v=5wCK6XGC3ig.

Patek, Sheila. “Measuring the fastest animal on earth.”, 17 May 2007, TED, YouTube, https://www.youtube.com/watch?v=RHTTIg7HY80.

“Strandbeest Multi Tripodes”, 25 October 2020, theo jansen, YouTube, https://www.youtube.com/watch?v=nPqNVTj1o3sandfeature=emb_logo.

References

Academy, K. (n.d.). What is tension?. Retrieved from https://www.khanacademy.org/science/physics/forces-newtons-laws/tension-tutorial/a/what-is-tension

Altman, K. (2018). Mantis Shrimp—Pint-Sized Prizefighters. Retrieved from https://answersingenesis.org/aquatic-animals/mantis-shrimppint-sized-prizefighters/

Berkley, U. (n.d.). How smashing! Retrieved from https://ucmp.berkeley.edu/aquarius/raps.html

Bernasconi, S., Tordi, N., Parratte, B., Rouillon, J.-D., & Monnier, G. (2006). Effects of Two Devices on the Surface Electromyography Responses of Eleven Shoulder Muscles During Azarian in Gymnastics. Journal of strength and conditioning research / National Strength & Conditioning Association, 20, 53-57. doi:10.1519/R-16174.1

Britannica, E. o. E. (2015). Pantograph. In Encyclopedia Britannica. Retrieved from https://www.britannica.com/art/pantograph

Burrows, M. (1969). The mechanics and neural control of the prey capture strike in the mantid shrimps Squilla and Hemisquilla. Zeitschrift für Vergleichende Physiologie, 62(4), 361-381. doi:10.1007/BF00299261

Burrows, M., & Hoyle, G. (1972). Neuromuscular physiology of the strike mechanism of the mantis shrimp, Hemisquilla. Journal of Experimental Zoology, 179(3), 379-393. doi:10.1002/jez.1401790309

Carrara, P., Amadio, A. C., SerrÃO, J. C., Irwin, G., & Mochizuki, L. (2016). The cross on rings performed by an Olympic champion. Revista Brasileira de Educação Física e Esporte, 30(1), 71-77. doi:10.1590/1807-55092016000100071

Clippinger, K. S. (2016). Dance anatomy and kinesiology : [principles and exercises for improving technique and avoiding common injuries].

Dawkins, P. (2018). Quadric Surfaces. In. Paul's Online Notes. Retrieved from https://tutorial.math.lamar.edu/classes/calciii/quadricsurfaces.aspx

Dimery, R. (2019). The mantis shrimp packs the most powerful punch in the animal kingdom. Retrieved from https://www.guinnessworldrecords.com/news/2019/4/the-mantis-shrimp-packs-the-most-powerful-punch-in-the-animal-kingdom-567501

Foumberg, J. (2015). Anatomy of Theo Jansen's Strandbeest. Retrieved from https://www.chicagomag.com/Chicago-Magazine/December-2015/Anatomy-of-Theo-Jansens-Strandbeest/

Jansen, T. (2020). Strandbeest. In. https://www.strandbeest.com/explains

Katz, B. (2018). A Dracula Ant's Snapping Jaw Is the Fastest Known Appendage in the Animal Kingdom. Retrieved from https://www.smithsonianmag.com/smart-news/dracula-ants-snapping-jaws-are-fastest-known-appendage-any-animal-180971061/

Kumar, N. (2020). Prevalence of Osteoarthrosis.

Larabee, F. J., Smith, A. A., & Suarez, A. V. (2018). Snap-jaw morphology is specialized for high-speed power amplification in the Dracula ant, Mystrium camillae. Royal Society Open Science, 5(12), 181447-181447. doi:10.1098/rsos.181447

Levin, S. (2006). Tensegrity- The New Biomechanics. In (pp. 69-80). ISBN 978-0-19-967410-7

Levin, S. (2013). Closed kinematic chain mechanisms comprise the fundamental mechanics of biologic movement and stability.

Levin, S., de Solórzano, S. L., & Scarr, G. (2017). The significance of closed kinematic chains to biological movement and dynamic stability. Journal of Bodywork and Movement Therapies, 21(3), 664-672. doi:10.1016/j.jbmt.2017.03.012

Nahon, M. A., & Angeles, J. (1989, 1989/05/14/19). Force optimization in redundantly-actuated closed kinematic chains. Paper presented at the Proceedings, 1989 International Conference on Robotics and Automation.

NASA. (n.d.). Equilibrium of Forces. Retrieved from https://www.grc.nasa.gov/www/k-12/airplane/equilib.html

Oceana. (n.d.). Peacock Mantis Shrimp. Retrieved from https://oceana.org/marine-life/cephalopods-crustaceans-other-shellfish/peacock-mantis-shrimp

Patek, s. (2015). The Most Powerful Movements in Biology. American Scientist, 103, 330-337. doi:10.1511/2015.116.330

Patek, S. N., Korff, W. L., & Caldwell, R. L. (2004). Deadly strike mechanism of a mantis shrimp. Nature, 428(6985), 819-820. doi:10.1038/428819a

Patek, S. N., Nowroozi, B. N., Baio, J. E., Caldwell, R. L., & Summers, A. P. (2007). Linkage mechanics and power amplification of the mantis shrimp's strike. Journal of Experimental Biology, 210(20), 3677-3688. doi:10.1242/jeb.006486

Physiopedia. (n.d.). Kinetic Chain. In. https://www.physio-pedia.com/Kinetic_Chain

Pucheta, M. A., & Cardona, A. (2008). Synthesis of Planar Multiloop Linkages Starting from Existing Parts or Mechanisms: Enumeration and Initial Sizing. Mechanics Based Design of Structures and Machines, 36(4), 364-391. doi:10.1080/15397730802405929

Rhett, A. (2008). Why is the iron cross so difficult? In. https://www.wired.com/2008/08/the-iron-cross-or-why-is-gymnastics-so-darn-difficult/

Rivera-Brown, A., & Frontera, W. (2012). Principles of Exercise Physiology: Responses to Acute Exercise and Long-term Adaptations to Training. PM & R : the journal of injury, function, and rehabilitation, 4, 797-804. doi:10.1016/j.pmrj.2012.10.007

Roylance, D. (2000). Trusses In: Massachusetts Institute of Technology (MIT). Retrieved from http://web.mit.edu/course/3/3.11/www/modules/truss.pdf

Staff, C. C. (1959). The Hyperbolic Paraboloid. Retrieved from https://www.concreteconstruction.net/business/the-hyperbolic-paraboloid_o

Valero-Cuevas, F. J., Yi, J., Brown, D., McNamara, R. V., Paul, C., & Lipson, H. (2007). The Tendon Network of the Fingers Performs Anatomical Computation at a Macroscopic Scale. IEEE Transactions on Biomedical Engineering, 54(6), 1161-1166. doi:10.1109/TBME.2006.889200

van den Bogert, A. J. (2003). Exotendons for assistance of human locomotion. Biomedical Engineering Online, 2(1), 17. doi:10.1186/1475-925X-2-17

Wang, J., Gosselin, C. M., & Cheng, L. (2002). Modeling and Simulation of Robotic Systems with Closed Kinematic Chains Using the Virtual Spring Approach. Multibody System Dynamics, 7(2), 145-170. doi:10.1023/A:1014491204982

WebAssign. (2010). Equilibrium applications of Newton's laws of motion. Retrieved from http://demo.webassign.net/ebooks/cj8demo/cutnell3550/cutnell3550c04/cutnell3550c04-sec1-0011_ref.htm?__cf_chl_jschl_tk__=pmd_af231a1963dd738d9984485324ef864f01dee69c-1628632958-0-gqNtZGzNAnijcnBszQO6 Wiki, D. B. (2020, 9 Sept 2020). Hyperbolic paraboloid in construction. Retrieved from https://www.designingbuildings.co.uk/wiki/Hyperbolic_paraboloid_in_construction