Animal Communication: A Mathematical Review

Adam Khan, Janique Mayrand, Olivia Ouellet, Angela Wang

Abstract

Nature is composed of a variety of colours and rhythms.  Within these displays of color and rhythm exist patterns and relations, which have been studied and modelled to better understand existing relations and recurrences. In the animal kingdom, communication has evolved through both spontaneous and instantaneous patterns and relations, which can be mathematically represented. This paper will examine how the designs of these patterns respond to the principles of functionality and efficiency of animal communication. First, the visual use of bioluminescence will be explored, specifically the synchronous interactions between the male's signals and the female's response in fireflies. Next, pheromone-driven responses by male moths for interspecies communication is inspected using the male random flight model.  Subsequently, the vocalization of rock hyrax will be analyzed through syntactic analysis of hyrax songs. Finally, vocal signals will be evaluated through composite systems, focusing on the non-combinatorial response of putty-nosed monkeys. With the stunning variety of existing on Earth, there is unique forms of communication and thus these examples are simply a flavouring of the mathematics behind communication in the animal kingdom. 

Introduction

Communication may be one of the biggest factors contributing to the evolution of all species known to mankind.  Defending one's territory, acquiring resources, attracting mates, maintaining relationships, and more are achieved through communication. It may be strenuous for one to unravel the meaning of conspecific animal communication. For example, what is meant when dogs bark, bees dance, chameleons change color, or jellyfish light up. To further understand how and why animals communicate, mathematical models have been developed and reworked for a few decades. The objective is to find mathematical equations that model components of communication such as the frequency of chirps, the rhythm of calls, the frequency of light emission, and more. Successful modeling allows for better comprehension of the evolution of a species communication as well as its behavior. Although many mathematical models for animal communication have been created, new and improved models continue to be worked on.

This paper will present mathematical models pertaining to four distinct animal species, namely, fireflies, moths, the rock hyrax, and the putty-nosed monkey.

Bioluminescence

Certain animal species can produce light energy through chemical reactions occurring within the organism, a phenomenon known as bioluminescence (Branham, 2005). An excellent and fascinating example is fireflies (Fig. 1). They flicker their light which is produced through a chemical reaction involving the bioluminescent enzyme luciferase. A firefly's flashing sequence is controlled internally by the production of oxygen which plays a role in determining the rate at which the bioluminescent enzyme is synthesized.

The light signals produced by fireflies allow for efficient communication between conspecifics, especially when it comes to mating. Identifying members of the same species is also accomplished through light flickering signals as each species produces its unique sequence of light patterns. This section of the paper will focus on communication between male and female fireflies during the mating season. More precisely, the synchronization of male flickering patterns will be discussed using mathematical models and the females' response will be studied. Before continuing, however, the firefly life cycle will be discussed briefly. 

Firefly Life Cycle

The life cycle consists of four stages, namely, egg, larva, pupa, and imago. Females lay their eggs during the middle of the summer, and they hatch approximately four weeks later (Hadley, 2019). At this point, the larvae stage begins, which typically lasts all winter until pupation occurs in the spring. During the pupal stage, the firefly will undergo physical changes allowing for transformation into an adult.  In the adult stage, the former larvae are now considered fireflies. The adult stage is very short in duration, lasting for approximately two weeks long, and therefore, the sole purpose is to mate. The adult stage also corresponds to the short period in the summer during which one can observe many fireflies. Thus, efficient male to female communication is crucial to the survival and evolution of the firefly species as their mating opportunities occur in a short time span. 

Synchronization of Male Firefly Signals

Male fireflies can synchronize their light signals to aid females in the recognition of potential mates. Males will hover above females and flicker their lights, while females remain on the ground and respond if they feel compelled. Efforts to create mathematical models of the synchronous behavior of male fireflies have been made over the past few years and may be of interest when studying conspecific communication.

In order to model the synchronous behavior of male fireflies, it is necessary to consider each organism as an oscillator, which follows the equation below (Ermentrout, 1991):

\frac{d \theta}{dx} = \omega + P(\frac{t}{\tau}) \Delta \theta

where ω is the intrinsic frequency, P(t/τ) is the periodic forcing stimulus, and Δθ is the phase response curve.

The phase responsive curve (PRC) demonstrates the oscillator's change in phase shift induced by a signal as a function of the time of signalization. The curve assumes that T₀ is the natural period, in units of time, of the oscillator and we let t = t₀ ∈[0, T₀). The signals occur periodically; that is, they occur at t = T(t₀), T(t₀) + T₀, T(t₀) + 2T₀, … The change in the natural period of the oscillator from T₀ to T(t₀) only affects the following cycle. Each cycle is its own independent event. Thus, the phase response curve is defined as follows (Ramírez-Ávila et al., 2019):

\Delta \theta = \frac{T_{0}-T(T_{0}\theta)}{T_{0}}

where θ is the phase of the signal.

This implies that a change induced to the oscillator will result in a phase change, that is either a delayed signal or an early signal. This leads to Buck's phase resetting model.

The phase resetting model designed by Buck aims to explain how male fireflies are capable of spontaneously synchronizing their signals. It relies on the fact that a firefly's light emission frequency is affected by surrounding light energy, i.e., the light flashes from surrounding fireflies. Fireflies can thus adjust the frequency of their light signals by either increasing or decreasing the time between flash periods (Fig. 2) with the objective of attaining a flash rhythm similar to surrounding males.

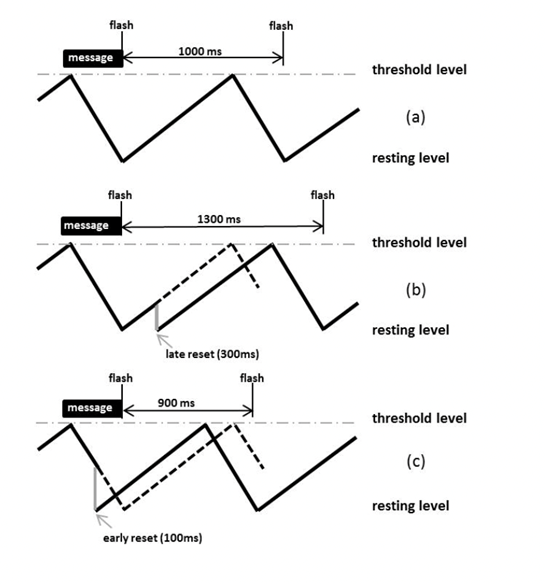
Female Response

Females will also produce light frequency patterns to inform males of their interest in courtship. These can be modeled by assuming that the signals are oscillators; however, the parameters of the female oscillators differ significantly from those of males. The model graphs the voltage as a function of time for the silent stage, discharging stage, charging stage and the flash stage (Fig. 3). An electronic firefly circuit (Chuang et al., 2004) is created using resistors, capacitors, a battery, a switch, a phototransistor, and lights, which models the flash signal sequences of fireflies. The design allows for increase or decrease in discharging time induced by lights in the electrical circuit. Thus, the circuit models the synchronous behavior of fireflies. The oscillators are set-up to automatically reset to the same state after reaching the threshold voltage (V_upper), that is, they reset to the lowest voltage (V_lower).

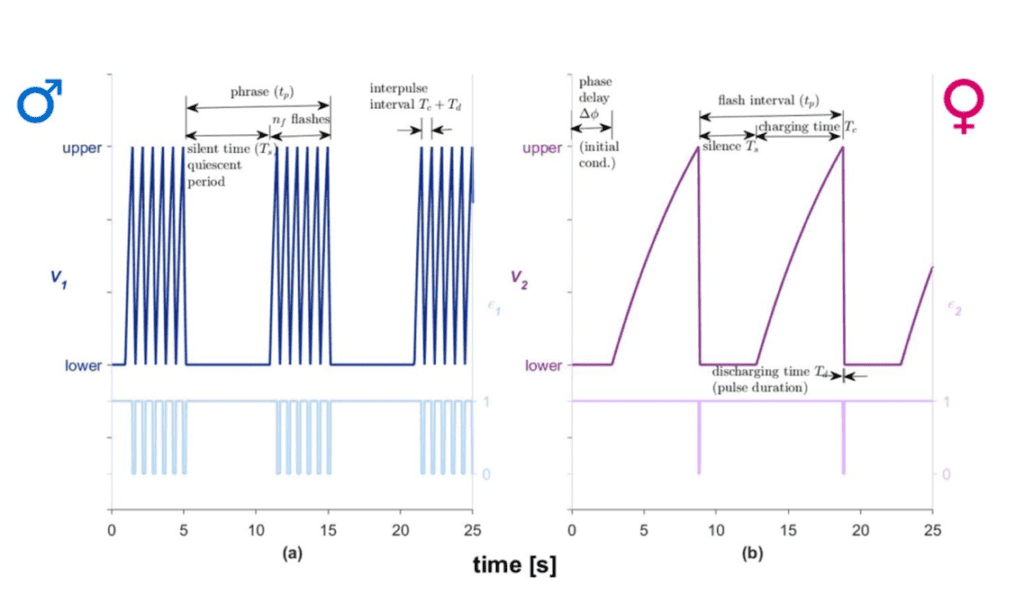
As demonstrated in Figure 3, the female's response differs from the male response in terms of the number of emitted flashes and the required charging and discharging times. Silent time is modeled to take into account the time during which the firefly is not flashing.

Moth Pheromones

Moths (Fig. 4) utilize semiochemicals called pheromones for interspecies communication. Each pheromone emitted by a conspecific triggers a physiological effect to it's surrounding conspecifics (Fleischer & Krieger, 2018). Female moths will emit their sex-specific pheromone through the release of a plume, a blend of chemicals. The plume of pheromones is spread in the air and male moths will then detect it using their antennae which will lead to a physiological response, where they begin flying towards the female in order to mate (Stepien et al., 2020).

Communication involves both the sending of the information, i.e., the production of the pheromones by the female, as well as the reception of the information, i.e., the detection of the pheromones by the male antennae. Communication does not occur without both. Stepien et al. (2020) developed a mathematical model, called the Male Random Flight Model, that models male moths random search for female moth pheromones. Therefore, this is a model of the reception aspect of communication.

First, all the variables will be explained.

c(x,t) = concentration of the female emitted pheromone plume in two dimensions

This model is in two dimensions, meaning the female and male moth are on the same plane at a fixed altitude. This is the case because in some experimental studies there was little vertical motion in male moths. c(x,t) is a concentration that varies in space and in time, as it varies with wind currents and the rate at which the pheromones are emitted by females (Stepien et al., 2020).

C_tol = the threshold pheromone concentration that male moths can detect

Male moths can detect the pheromone plume c(x,t) once it surpasses a certain threshold C_tol. C_tol represents how sensitive a male moth is to the pheromones released by the female and can thus vary from male to male and from species to species. A lower C_tol value indicates that a male moth is more sensitive to pheromones and thus requires a lower concentration to detect it. This models real life as male moths come with antennae of varying lengths and complexities and a moth with a longer/more complex antennae will be able to better detect pheromones and thus have a lower C_tol value (Stepien et al., 2020).

Ω(t) = the trapping region

The trapping region is the area in which c(x,t) is greater than or equal to C_tol; in other words, this is the region where the concentration of pheromones is larger or equal to the value needed for it to be detected by a particular male moth. For a male moth with a lower C_tol value, the trapping region is larger, and a larger trapping region means the moth is more likely to sense the pheromone and mate with the female (Stepien et al., 2020).

D = diffusion constant of male flight

When moths are outside of the trapping region, they are in two-dimensional random flight unaffected by the plume. This random flight is with diffusion constant D. A larger D means a more motile moth and is thus likely to find the pheromone plume faster than a moth with smaller D. C_tol and D in nature have an inverse relationship, as a larger C_tol generally indicates that a moth has a larger antenna, and a larger antenna reduces the moths mobility and thus reduces its D value (Stepien et al., 2020).

g(x,t) = probability density function

g(x,t) is the probability density function that a moth is at point x=(x,y) outside the trapping region Ω(t) at time t. In this model, the male moth is assumed to originally be outside of the trapping region (R²\Ω(t)). Note that the function g(x,t) is dependent on the trapping region (which is itself dependent on C_tol and c(x,t)) and the diffusion constant.

Once the moth reaches the trapping region boundary (i.e., once the moth detects the pheromone plume), random flight stops and the moth surges towards the female.

This formula represents the probability that a male moth has not sensed a pheromone plume released by a female moth at time t (Stepien et al., 2020). Note that the integral is defined over a two-dimensional region and therefore, does not have an upper bound. The lower bound represents the domain of integration.

P(t) = \int_{\mathbb{R}^2/\Omega(t)}g(x,t)dxdy

And this formula represents the probability that a male moth has sensed a female moth pheromone plume at time t:

C(t)=1-P(t)

One can graph P(t) and C(t) to show how they vary with time with constant D and Ω(t) (Fig. 5)

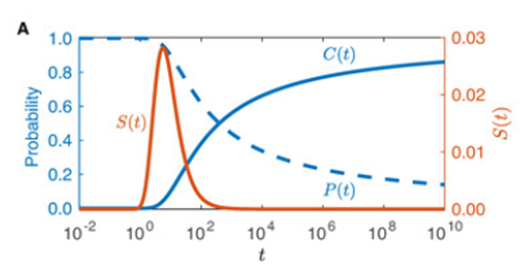
Stepien et al. (2020) developed this model further, including more and more factors to develop a precise mathematical model, but even this first relatively simple model allows us a greater understanding of female to male moth pheromone communication.

Syntactic Analysis of Rock Hyrax (Provocavia Capensis) Vocalizations

Rock hyraxes (Fig. 6) are the closest terrestrial relatives of the elephant (Deraniyagla, 2020).They are highly social animals that live in colonies of around 50 individuals, and they inhabit rocky outcrops across East Africa, the Arabian Peninsula, Israel, and Lebanon (The Editors of Encyclopaedia Britannica, 2021). This species is capable of generating only five discrete vocal elements or ‘syllables' (tweet, squeak, wail, chuck, and snort), but they combine them in syntactically complex ways (Kershenbaum et al., 2012).

Hyrax males, in particular, are known to produce elaborate vocalizations called ‘songs' lasting several minutes in duration. Each song consists of continuous syllabic stretches or ‘bouts', each of which is separated by a brief pause. The first bouts of a hyrax song are typically short and simple (i.e., approximately 6 syllables in length), while subsequent bouts are increasingly more complex and prolonged, with the last few bouts of the song surpassing 30 syllables in length (Kershenbaum et al., 2012). Although the role of hyrax songs is not precisely understood, a striking parallel exists between the structure of these songs and the musical concept of a crescendo. As such, hyrax songs likely advertise the fitness of high-ranking males within the colony (Demartsev et al., 2014).

In this section, the ordering, or syntax, of vocal syllables in rock hyrax songs will be discussed from the perspective of information theory. Such a treatment will reveal the presence of regional ‘dialects' of hyrax vocalizations which in turn suggests that this species is one of the few mammals outside of primates, cetaceans, pinnipeds, and bats that are capable of vocal production learning (Kershenbaum et al., 2012).

Metrics for Syntactic Analysis

In a 2012 study by Kershenbaum et al., the songs of rock hyraxes were sampled and analyzed in nine regions around Israel, each of which contained several sites. To compare the syntactic profile of hyrax songs between different sites and regions, three metrics were computed: Needleman-Wunsch (NW) distance, Mutual Information (MI), and scaled Euclidean Genetic Distance (D_R).

NW-distance measures the degree of dissimilarity between two strings. Here, a string is the syllabic representations of a hyrax song. An elevated NW-distance signifies great divergence of hyrax song syntax. The NW algorithm incrementally shifts the alignment of the two strings to achieve the minimum number of pointwise differences; that is, it shifts the alignment of the strings until they are as similar as possible. The NW-distance is this minimum number of differences (Kershenbaum et al., 2012; Kellis et al., 2020).

MI, on the other hand, measures both string similarity and complexity. The MI of two hyrax songs A and B is determined by the formula

MI(A,B)=H(A)+H(B)-J(A,B)

where H is the Shannon entropy function of a stream, and J is the joint entropy function of the two streams. These functions are defined as

H = -\sum p(x)log(p(x))

J(A,B)=- \sum p(x,y)log(p(x,y))

where p(x) is the probability of syllable x occurring in the stream, and p(x,y) is the probability of two syllables x and y occurring at the same point in the two streams (Kershenbaum et al., 2012; Markowsky, 2017). X and y can be the same syllable, or different. As per this formulation, two hyrax songs A and B that are nearly identical and syntactically complex would yield a high MI score.

Finally, D_R measures the song dissimilarity between two hyrax populations at sites a and b (Kershenbaum et al., 2012). This last metric is defined as

D_{R}(a,b)= \frac{1}{M} \sum_{j=1}^{M} \sqrt{ \frac{1}{2} \sum_{i=1}^{M} (p_{ij}-q_{ij})^2 \frac{n_{j}}{\sum n_{j}} }

To calculate D_R, the hyrax songs at both sites were divided into M loci where locus j consists of n_j consecutive syllables (see the equation above). The variables p_ij and q_ij simply denote the frequencies of syllable i in locus j where p_ij is specifically associated with the population at site a while q_ij is associated with the hyrax population at site b (Kershenbaum et al., 2012).

Syntactic Analysis and Significance

After syntactic analysis was performed, it was found that NW correlates positively with geographic distance over short distances, while MI correlates negatively (Fig. 7, Fig. 8). However, there was no correlation over large distances. In addition, the average D_R between populations belonging to different regions surpassed the average D_R between hyrax populations within the same region (0.021+/-0.0005 as opposed to 0.019+/-0.001). These findings indicate that hyrax songs from different regions of Israel are syntactically unrelated, thus forming separate ‘dialects,' whilst a ‘dialect continuum' exists between the closely-situated sites of any particular region (Kershenbaum et al., 2012).

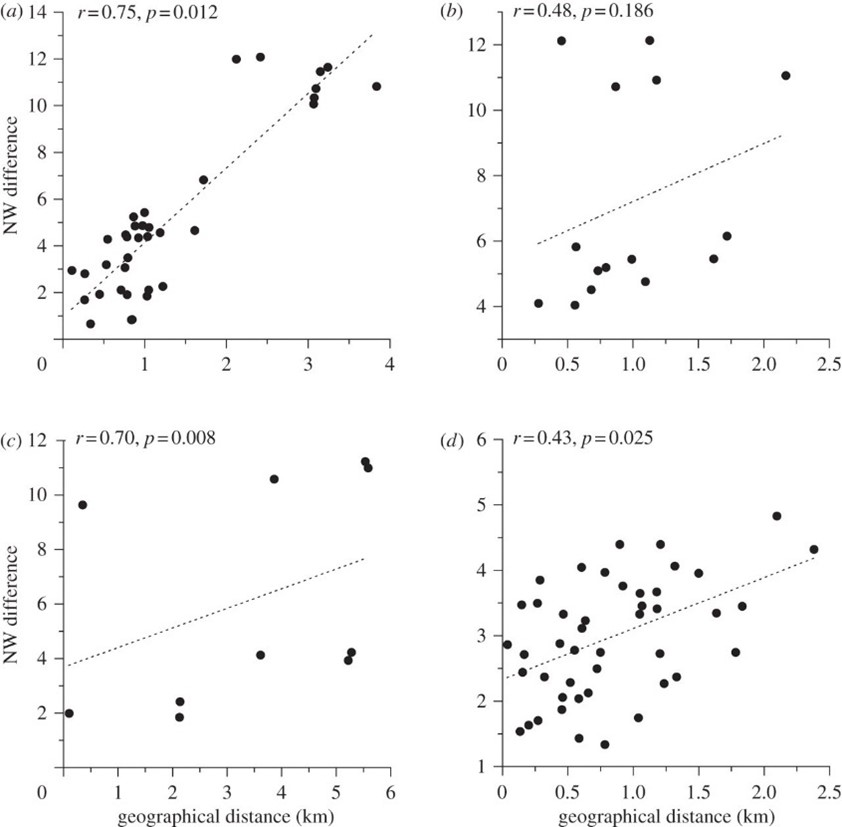
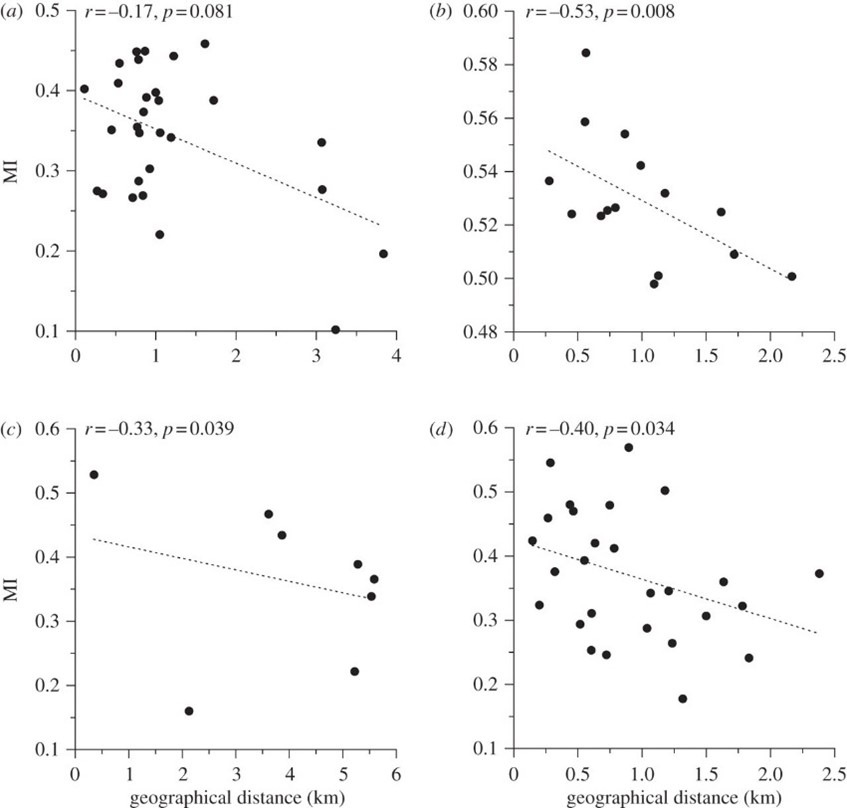
These findings are significant because they suggest the existence of vocal production learning (VPL) in rock hyraxes (Kershenbaum et al., 2012). VPL refers to the ability of a species to modify their vocalizations after hearing those of conspecifics or of other species, and it is considered a key feature of complex, human-like communication (Janik & Knörnschild, 2021; Kershenbaum et al., 2014). In the case of rock hyraxes, dominant males have the greatest propensity to sing, and these males are also known to immigrate to nearby colonies. It is therefore plausible that immigrant males transmit aspects of their native dialect to resident males of the colony to which they have immigrated. This phenomenon, in combination with the fact that hyraxes do not disperse over distances greater than 5 km, would explain the existence of unrelated regional dialects and local, continuous syntactic variations (Kershenbaum et al., 2012). However, syntactic analysis alone does not provide incontrovertible evidence of the existence of VPL in this species as genetic factors could potentially influence the syntax of rock hyrax songs. Thus, to definitively establish VPL, observations would need to be made of syntactic changes following the introduction of a ‘foreign' male to an otherwise isolated colony (Kershenbaum et al., 2012; Janik & Knörnschild, 2021).

Composite Auditory System

Communication is known to be built upon the interpretation of signals, oftentimes more than one, affecting the expression of ideas and emotions. In environments, such as in dense rainforests where there is limited long-range visibility, auditory communication predominates amongst species. To maximize the vocal range, animals reutilize existing singular repressions to form composite language through concatenation and repetitions of sounds. These composite language formations can be divided into different systems of interpretation through non-combinatorial and combinatorial communication.

Defining Non-Combinatorial Communication

Vocal language is provoked by the surrounding environments. To communicate, animals use sounds, referred to as a signal. Signals can be individually analysed and each signal triggers an effect/ response (Scott-Phillips & Blythe, 2013). In a non-combinatorial communication system, two (or more) holistic signals are combined to form a third, composite signal (Fig. 9).

This non-combinatorial system of communication, straightforward as it might seem, is repetitive and losses efficiency due to the need to create new vocal terms to express new distinct messages. The rare system of combinatorial communication is a solution to reduce repetitions.

Combinatorial Calls in Putty-Nosed Monkeys

The putty-nosed monkey, Cercopithecus nictitans (Fig. 10), occupy the dense rainforests of Central and Western Africa. This species heavily relies on tribe protection from vicious predators, such as leopards and eagles (Covert, 2019), and collaboration for scavenging through effective vocal-signal based communication.  

A vocal signal can be either a singular “call”, emission of sound which correlates to a certain known message, or concatenation of singular calls. Putty-nosed monkeys can concatenate singular calls into a vast variety of sequences with different interpretations, in a non-restrictive manner of combinatorial communication.

The putty-nosed monkey combinatorial call system can be modelled most prominently by its “pyow-hack” call. The A: “pyow” and B: “hack” calls, onomatopoeias for actual sounds, can both be considered individually. In an environment where leopards are present (Fig. 11, state of world a), a putty-nosed monkey will signal through a “pyow” call (A). In response, the other monkeys will climb up in the trees (X effect) to protect themselves from the leopards. Similarly, the “hack” (B) occurs when eagles are present, b. Upon reaction of the “hack”, the monkey with climb down the trees (Y) to hide in the bushes, away from the eagles. When the concatenation of these calls occurs, “pyow-hack”, C=A+B, by combinatorial communication implementation, this does not allude to a state where any eagles and leopards are present, c ≠ a + b. It is not observed that the reaction will be X+Y, Z ≠ X + Y. Instead, in a state where food is in shortage during scavenging or the current habitation is no longer adequate (state c), the putty-nosed monkey will signal the sound “pyow-hack.” This alerts the others to Z: move to a new location (Scott-Phillips & Blythe, 2013).

By the putty-nosed “pyow-hack” modelling, it is revealed that language usage does not need to hold symmetrically properties. This allows for fewer calls to express a set number of possible messages, allowing for expansive communication.

Although a combinatorial system of communication is more advantageous for wider possibility of expression, it is rare in nature due to its lack of interdependence of signals and response. For new combinatorial composites to emerge, prolonged external triggers must exist to allow for adaptations of the new mutual understanding of the composite form of communication (Scott-Phillips & Blythe, 2013). When expanding expression using vocal language, animals are more likely to implement the non-combinatorial system of a symmetrical existing signal and effect composite, as it builds upon existing understandings of individual pairing of signal and effect.  

Conclusion

Mathematics and biology are disciplines that have traditionally been considered disparate despite the fact that mathematics is an essential tool in other areas of science. Throughout this review, the power of mathematical modelling as it pertains to animal communication has been illustrated through a variety of examples. To begin, the bioluminescent communication between male and female fireflies during mating season was discussed from the perspective of mathematical oscillators. This led to the formulation of Buck's phase resetting model and the electronic firefly circuit. Subsequently, mathematics was applied to explain the pheromonal communication of moths. Thereafter, techniques from information theory were applied to the syntax of rock hyrax songs to reveal regional ‘dialects' and the possibility of vocal production learning in this species. Finally, combinatorial communication was examined with particular emphasis on the vocalizations of the putty-nosed monkey. In each of these examples, mathematical models help to describe the underlying communication method whilst also suggesting avenues of further study. In the future, these models will surely be refined and reworked to provide even deeper insight into the intricacies of animal communication.

References

Branham, M. (2005, September 5). How and why do fireflies light up? Scientific American. https://www.scientificamerican.com/article/how-and-why-do-fireflies/

Chuang, T.-H., Chang, C.-Y., Byerly, J., & Slattery, C. (2004, June 7). Distributed Synchronization of Electronic Fireflies. Dept. Electrical and Computer Engineering, Ohio State University. https://www2.ece.ohio-state.edu/~passino/fireflyfolder/EE683report.pdf

Covert, T. (2019, August). Putty-Nosed Monkey. New England Primate Conservancy. Retrieved November 25, 2021, from https://neprimateconservancy.org/putty-nosed-monkey/

Demartsev, V., Kershenbaum, A., Ilany, A., Barocas, A., Bar Ziv, E., Koren, L., & Geffen, E. (2014). Male hyraxes increase song complexity and duration in the presence of alert individuals. Behavioral Ecology, 25(6), 1451-1458. https://doi.org/10.1093/beheco/aru155

Deraniyagala, P. E. Pieris. (2020, April 5). proboscidean. Encyclopaedia Britannica. Retrieved November 26, 2021, from https://www.britannica.com/animal/proboscidean

Dizikes, P. (2019, September 3). Old World Monkeys Vocalizations May Be More Sophisticated Than Previously Realized. SciTechDaily. https://scitechdaily.com/old-world-monkeys-vocalizations-may-be-more-sophisticated-than-previously-realized/amp/

Ermentrout, B. (1991). An adaptive model for synchrony in the firefly Pteroptyx malaccae. Journal of Mathematical Biology, 29(6), 571-585. https://doi.org/10.1007/bf00164052

Hadley, D. (2019, October 6). The 4 Stages of the Firefly Life Cycle. ThoughtCo. Retrieved November 26, 2021, from https://www.thoughtco.com/life-cycle-fireflies-lightning-bugs-1968137

Janik, V. M., & Knörnschild, M. (2021). Vocal production learning in mammals revisited. Philosophical Transactions of the Royal Society B: Biological Sciences, 376(1836), 20200244. https://doi.org/10.1098/rstb.2020.0244

Kellis, M. et al. (2021, March 17). 2.5: The Needleman-Wunsch Algorithm. LibreTexts. Retrieved November 26, 2021, from https://bio.libretexts.org/Bookshelves/Computational_Biology/Book%3A_Computational_Biology_-_Genomes_Networks_and_Evolution_(Kellis_et_al.)/02%3A_Sequence_Alignment_and_Dynamic_Programming/2.05%3A_The_Needleman-Wunsch_Algorithm

Kershenbaum, A., Bowles, A. E., Freeberg, T. M., Jin, D. Z., Lameira, A. R., & Bohn, K. (2014). Animal vocal sequences: not the Markov chains we thought they were. Proceedings of the Royal Society B: Biological Sciences, 281(1792), 20141370. https://doi.org/10.1098/rspb.2014.1370

Kershenbaum, A., Ilany, A., Blaustein, L., & Geffen, E. (2012). Syntactic structure and geographical dialects in the songs of male rock hyraxes. Proceedings of the Royal Society B: Biological Sciences, 279(1740), 2974-2981. https://doi.org/10.1098/rspb.2012.0322

Kim, S. E. (2021, July 19). These Moths Are So Gorgeous They ‘Put Butterflies to Shame'. Smithsonian Magazine. https://www.smithsonianmag.com/science-nature/celebrate-national-moth-week-observing-these-diverse-and-beautiful-insects-180978218/

Markowsky, G. (2017, June 16). information theory. Encyclopaedia Britannica. Retrieved November 26, 2021, from https://www.britannica.com/science/information-theory/Classical-information-theory

Ramírez-Ávila, G. M., Kurths, J., Depickère, S., & Deneubourg, J.-L. (2019). Modeling Fireflies Synchronization. In (pp. 131-156). Springer International Publishing. https://doi.org/10.1007/978-3-319-78512-7_8

Scott-Phillips, T. C., & Blythe, R. A. (2013). Why is combinatorial communication rare in the natural world, and why is language an exception to this trend? Journal of The Royal Society Interface, 10(88), 20130520. https://doi.org/10.1098/rsif.2013.0520

Stepien, T. L., Zmurchok, C., Hengenius, J. B., Caja Rivera, R. M., D'Orsogna, M. R., & Lindsay, A. E. (2020). Moth Mating: Modeling Female Pheromone Calling and Male Navigational Strategies to Optimize Reproductive Success. Applied Sciences, 10(18), 6543. https://doi.org/10.3390/app10186543

The Editors of Encyclopaedia Britannica. (2021, October 19). hyrax. Encyclopaedia Britannica. Retrieved November 26, 2021, from https://www.britannica.com/animal/hyrax