Courtship and Mating Within Evolutionary Game

Liam Fetherstonhaugh, Joseph Grotsky, Chloe Jacquet, Samuel Nidelli

Abstract

In this essay, we investigated methods of mathematical modeling which can be utilized to describe evolutionary game theory. An organism’s evolutionary fitness is defined by their ability to pass their genes on to their offspring. Without effective courting and mating practices, it is impossible to find quality mates and therefore pass on genetic material. Therefore, their fitness is directly contingent on every choice they make in courtship and mating. Their decisions can be modeled through game theory each with different outcomes. We will discuss how these models can explain the genetic advantages of monogamy, why it is worthwhile for certain animals to be selective with mates, and why an organism would handicap themselves to increase long-term benefit. Additionally, we will discuss how game theory can be applied to decrease vector-borne diseases without contaminating natural resources and harming biodiversity.

Introduction

Animal courtship behaviour can be extremely complex, convoluted, and, at first glance, inexplicable. These behaviours often defy traditional assumptions of Darwinian evolution about what would be best for the animal’s survival and reproductive success. The solution to understanding these behaviours, to explain the inexplicable, was proposed by mathematical biologist John Maynard Smith in 1984, who applied game theory to model the benefits of certain behaviours in the context of evolution. Game theory is a way to mathematically model interactions and decisions of multiple ‘players,’ and what outcome results from these choices under different conditions, the ‘game,’ in order to understand why certain decisions are made. Through applying these types of models to animals, the value of these courtship behaviours and characteristics can be exposed, allowing them to be further studied and applied for other uses.

G function framework within Darwinian Dynamics and Evolutionary Game Theory

Evolutionary game theory’s direct link with courtship and mating is how it models which specific genes, behaviours, adaptations, and related factors will best suit the environment of a certain organism. This will inherently monopolize this specific trait throughout the population, all with the goal of aiding the species in its survival. Many different types of functions have been theorized to describe population dynamics in evolutionary game theory. One major example is the replicator equation, which was first theorized by Taylor and Jonker in 1978, or replicator dynamics, where a ‘replicator’ is an evolutionary entity, for example, a gene, a technique, a behaviour, etc., that gets copied through evolution because it generates payoffs (“Replicator dynamics,” n.d.). Replicator equations and G functions are sets of differential equations used to model Darwinian dynamics, which are population and strategy dynamics coupled together (Bukkuri et al., 2021).

To properly demonstrate that G-functions can apply to advanced models, the three ‘tenets’ of Darwin’s theory of evolution (natural selection) must be discussed (Bukkuri et al., 2021). The three “tenets” are shown by the following: there must be a heritable variation, which is the genetic variance of individuals (Bijma, 2011), there must be a struggle to stay alive, and the heritable variation influences the struggle (Bukkuri et al., 2021). The goal of the G function is to “describe the per capita growth rate of individuals of an evolutionarily identical group, removing the need to define different functions for evolutionarily identical individuals that use different strategies” (Bukkuri et al., 2021). The fundamental principles of the G-function are the heritable variation, which represents the heritable strategy, u_i, which is a part of the set U and the ‘tenet,’ struggle for existence, is denoted by the fitness generating function, G(v, u, x)|_v=ui, where strategies influence the per capita growth rate (Bukkuri et al., 2021). The parameters v, u, and x are interpreted by the following: v, “strategy of focal member;” u, “vector of strategies of all members;” and x, “vector population size of all Members” (Bukkuri et al., 2021).

Equations (1) and (2) form the G function framework which is used to describe population and strategy dynamics. Knowledge of the fitness generating function is multiplied by the current population (x_i), which gives the formula for population dynamics (1).

\frac{dx_{i}}{dt} = x_{i}G|_{v = u_{i}} \space \space \space \space \space \space (1)

In Equation (2), the strategy dynamics is formulated, which describes how the populations traits will change over time (Bukkuri et al., 2021). The variable σ_i² is defined as the additive genetic variance and heritability (Bukkuri et al., 2021). This parameter demonstrates the rate at which traits within the species will change (mutation, behaviours, population structure, etc.) (Bukkuri et al., 2021).  

\frac{du_{i}}{dt} = \sigma_{i}^{2} \frac{dG}{dv}|_{v = u_{i}} \space \space \space \space \space \space (2)

All in all, population and strategy dynamics make up Darwinian dynamics and demonstrate the payoffs of specifics adaptations and/or behaviours within a certain population. Note that equations (1) and (2) depict the simplest of Darwinian dynamics, since they contain only one G function (Bukkuri et al., 2021). More complex models can be theorized when more than one G function is needed.

Using Coyness Game to Optimize Mating Opportunities

As discussed before, evolutionary game theory’s link with courtship and mating is to find traits, whether they be behaviours, adaptations, genes, or something else, that will augment a population’s chance of survival. A specific trait that is sought after within female species when choosing a mate is the likelihood that the male species will help raising the young (McNamara et al., 2008). To properly evaluate a male’s likelihood to help raise the young, the female will be coy, to delay the courtship process. In this game, there are 4 possible combinations since the male and female only have 2 options for potential strategies regarding raising the young (McNamara et al., 2008). The females can either be fast or a coy and the males can either be faithful or philanderers (McNamara et al., 2008). A model was developed by Wachtmeister et al. (1999) to find the amount of time that is the most strategically advantageous for the females to wait before mating. Equations (3) and (4) summarize the model, where W_s,t is the “expected fitness of a female postponing reproduction in state (s,t)” and R_s,t represents the “expected fitness of a female starting reproduction in the same state” (Wachtmeister et al., 1999).

W_{s,t} = (G_s(s) + (1-q)(1-G_C(s))) F(s+1, t+1, T) + q(1-G_C(s))F(0, t+1, T), s>0 \space \space \space \space \space (3)

R_{s,t} = G_C(s)e^{-rt} + (1-G_C(2)) \delta e^{-rt}, s>0 \space \space \space \space \space (4)

The variable s is the pairing time, t is the time of season, T is the time of breeding season, G_c(s) is the probability of being paired with a faithful male, q is the probability a female does not court with a philanderer, δ is a deception factor if the male is a philanderer, F is the maximum reproductive success, and e^-rt rate at which reproductive success declines (Wachtmeister et al., 1999). Results show that coyness is at its highest rate when the most unfaithful males are present. For example, 2/3 of Ficedula hypoleuca (Fig. 1) try and mate with a second female, but only 10-15% succeed (Wachtmeister et al., 1999).

Explaining Mate Choice with Game Theory

Mate choice is a driving force in the evolution of many species through the sexual selection of different desirable traits (Edward, 2014). Different species exhibit different mate choice systems that may not seem to be evolutionarily favourable, but through modelling these systems using game theory the advantages become clear.

Using standard sexual selection theory, it makes the most sense for a male individual to be promiscuous and mate with many females to increase reproductive success (Fromhage et al., 2008). However, certain species are known to exhibit monogyny, where the male will only have one mate in its lifetime, while the female may have many. The value of this mating tactic can be modelled using game theory. One model developed by Fromhage et al. (2008) seeks to explain in spider species where biological constraints lead to only monogyny and bigyny (where males mate with two females) being viable why one may be favoured over the other (Fig. 2). Their complex mathematical model considers many different parameters, including the probability of a female to experience a mating attempt, the success rate of a male to mate with any given female, the probability of fertilization, and many more, to compare the reproductive success of monogynists and bigynists. They developed equations (5) and (6) to model the reproductive success of monogynists, w_m, and bigynists, w_b, respectively, as a function of these variables and found under which parameters one is greater than the other.

w_m = \frac{ (1-poi(c_m,0)) \sum_{i=1}^\infty \sum_{j=0}^\infty F_{ij}(xi/(xi+j)) }{pTSR} \space\space\space\space\space (5)

w_b = \frac{ poi(c_m,0)(1-poi(c_b,0)) +  (1-poi(c_m,0)) \sum_{i=1}^\infty \sum_{j=0}^\infty F_{ij}(j/(xi+j)) }{(1-p)TSR} \space\space\space\space\space (6)

Through this model, Fromhage et al. (2008) found that there are different conditions under which monogyny or bigyny will be favoured. Under the condition that monogynist and bigynist males have the same amount of ejaculate, and thus monogynist males transfer double the amount a bigynist does to an individual female, monogyny will be favoured if there are more males than females in the population, i.e., the tertiary sex ratio is male leaning, otherwise, bigyny will be favoured. This is because an increased male to female ratio results in increased paternity share competition, which is where if multiple males mate with a single female, only a fraction of her eggs will be fertilized by any one of the males. This makes it a valuable investment for a male to repeatedly mate with a single female to increase their paternity share, even at the cost of losing a potential chance to mate with another female, resulting in increased success of monogynist males. If the tertiary sex ratio is more balanced, there is less chance that a male’s paternity share will be challenged, making it a poor investment to stay with a single mate, increasing the success of bigynist males. The more that the tertiary sex ratio leans towards males, the more successful the monogynist male spiders will be over the bigynists, and vice versa. The success of monogynist or bigynist males determines which of the two are more likely to pass on their genes, directing the evolution of the species in one direction or the other.

Another prediction of sexual selection theory is that in most species, it is females who are able to choose which male to mate with because males are able to reproduce at a greater rate and thus do not need to be as selective. This prediction holds in most cases, but cases of reversed male mate choice and mutual mate choice have also been exhibited by certain species under specific conditions (Venner et al., 2010). To understand why this occurs in nature, researchers have used game theory to develop theoretical models of mate choice. A model developed by Venner et al. (2010) has been used to show what conditions lead to a switch between a female mate choice system and a male mate choice system. They analyzed how a male’s choosiness of a mate is dependent on variables like the amount of competition from other males, their own strength to compete with other males, the fertility of the females, and the difference in quality between the ‘best’ and ‘worst ‘quality females (based on fertility). The game considers that the male will, for a set time, guard a potential mate against competitors before mating, and then will leave after mating. At any point while the male is guarding the female, a competitor can challenge the guarding male. If successful, the new male will take over guarding the female and the same cycle will repeat until one male is successful in defending the female long enough to mate with her. Being removed from guarding a potential mate before being able to mate with her will result in a lost investment of time and effort with no returns. A higher quality female will have more competition from males to mate with her. This means that a male will have to invest more into defending a high-quality female over a lower quality one and will have a higher risk of losing out on the reward of mating with her.

The game theory model by Venner et al. (2020) was used to determine in what cases that investment/cost plays a role in male mate choice and if it is worth it for the reward of mating with a high-quality female. Through this model, they created a rejection index that is used to ascribe a numerical value to the value a male gets from rejecting a potential mate based on several different parameters (Fig. 3). If males are predicted to have a positive rejection index for a given set of parameters (i.e., it is valuable for the male to reject the female), that is an indication of a male mate choice system. If the rejection index is negative, it would be disadvantageous for the male to be selective and reject the potential mate. The results of this model were that under the fixed condition that there is a very low chance of a female encounter due to a male biased tertiary sex ratio, the rejection index was negative for all other conditions, meaning even the most competitive males will mate unselectively with any female they come across. If the opposite is true, that there is a high probability of a male coming across a female, a male mate choice system can occur. The strongest males will only mate with the highest quality females regardless of other parameters. Under the same fixed condition of a high probability of coming across a female, the model predicted weaker males to selectively mate with high quality females if the investment of time required for mating was small. If the investment of time required was large, the opposite happened, and lower quality males were predicted to selectively mate with lower quality females due to the risk of a challenge from a stronger male when attempting to mate with a higher quality female. The model predicts this male mate choice system to become more pronounced if a risk of death from mating is considered.

The Handicap Principle in Evolutionary Game Theory

Evolutionary game theory is the extensive study of mathematical modelling to analyze individual behaviour in competitive scenarios. In the animal kingdom, this is used to describe tendencies, evolutionary traits, and actions specific to a species’ needs. One such notion is the handicap principle. Initially proposed by Amotz Zahavi, the handicap principle suggests characters will adopt inhibiting traits, or handicaps, in exchange for a more beneficial outcome (Zahavi, 1975). In courtship, these handicaps are analyzed by the selecting sex to determine the quality of a mate (Zahavi, 1975). For all cases, the organism intends to showcase its overall fitness, with inordinate displays acting as a cue for mating potential.

The handicap principle is supported by two quantitative models referencing phenotypic traits: the additive and multiplicative models. The additive model describes a situation in which animals perform a costly display in effort to deter opponents or predators from a more costly forthcoming (Nur & Hasson, 1984). Stotting in gazelles exemplifies such version and is discussed in detail in a succeeding section. The multiplicative model is applied to scenarios where an individual with more developed ornate traits trades survival potential for mating success (Nur & Hasson, 1984). One such example is antler size in dear. In both cases, the models illustrate a positive correlation between a handicap and the ability of an individual (Nur & Hasson, 1984). This proves useful in mating practices through which the sexual selector is able to discern prospects based on the breadth of their handicap. Nonetheless, the extent of an individual’s handicap is broad, and issues arise when equating its benefits. Overall, the success of a handicap is based on the relationship between the signalling cost, the benefits, and the manner in which the handicap is awarded (e.g., mating) (Bullock, 1999). Hence, we examine the principle at play below.

Stotting in Gazelles

Gazelles, Gazella sp., employ a unique defensive tactic in an effort to deter predators and demonstrate mating potential. Stotting is a behaviour that involves a gazelle jogging and jumping in a vertical direction when approached by predators (Fig. 4) (Nur & Hasson, 1984). Instead of immediately fleeing the scene, the gazelle engages in an ostentatious display in the face of danger. This expels valuable time and energy without distancing itself from the nearby predators (Nur & Hasson, 1984). However, this behaviour alerts predators of the gazelle’s overall fitness. Rather than running immediately, this intends to prevent a predator-prey chase from ever occurring (Bullock, 1999). In the face of the gazelle’s flaunting behaviour, a predator may decide that it is unable to catch its prey and abandon a pursuit. This proves beneficial to the gazelle and illustrates the handicap principle at play.

It is important to discern the benefit is multilayered. In one aspect, by investing a small amount of energy upfront, the gazelle may prevent an exhaustive chase. In another, the efforts of the gazelle, if successful, demonstrate its fitness to potential mates (Caro, 1986). The process is entirely based on the perception of health in nature. Predators are quite selective with their prey, generally going after the weakest animal, as it is the easiest catch. A feeble gazelle will thereby engage in a diminished stot in comparison to a strong counterpart. The likelihood of the feeble gazelle showing prey weakness is much higher than the strong gazelle. Coincidently, the feeble gazelle may be forced to deal with its predators, while the strong gazelle avoids them altogether.

The Benefits and Pitfalls of Deer Antlers

In an effort to achieve mating practice, deer, Cerviae sp., invest deeply into a handicapping trait that decreases survival. On a yearly basis, male deer initiate a considerable investment by drawing on calcium reserves to grow ornate antlers (Nur & Hasson, 1984). These antlers are used in fighting bouts amongst males to prove strength to potential mating partners (Fig. 5). Evidence suggests that fighting ability directly correlates with antler size, be it the larger the antlers, the stronger the fighter (Nur & Hasson, 1984). As mating success is dependent on competition between males, the deer with the largest antlers is the most sought-after mate. Now in contrast, antler size is observed to hinder a deer’s ability to function in the wild; often times, large antlers prevent the animal from escaping predators. Such dilemma can be related by the multiplicative model of the handicap principle (Fig. 6). In this case, the male deer adopt largely handicapping traits to prosper in mating practice. While this proves beneficial in passing on traits, it does serve as a detriment to survival probabilities. Hence, for the case of the deer it is assumed that mating is the ultimate goal in nature, more so than longevity in survival.

Revisiting Game Theory Based on the Handicap Principle

From a game theory perspective, the handicap principle can be related by a variety of mathematical formulas, some quite simple in nature, others expansive and complicated. In Jumping to Bold Conclusions (1999), Seth Bullock suggests that “signaling will be evolutionarily stable when the net cost of signaling varies inversely with the magnitude of the trait being advertised.” This means that individual animals with a more prominent handicap (i.e., deer with larger horns or gazelle who can stot higher) are better suited to showcase said trait. That is, less effort is required to display their handicap than an inferior counterpart, who must exert more energy to make up for its deficiencies. Coincidently, game theory suggests that superior animals shall benefit from signalling more, as their intended response will be more frequent (Bullock, 1999). In contrast, bluffing from an inferior counterpart will be detrimental; by amplifying a handicap, the animal will find itself, at best, in a Pyrrhic victory (Bullock, 1999). This goes hand in hand with the principle of survival of the fittest. The animals most readily able to showcase their handicap are perceived to be the fittest, and best suited to pass on their traits by mating.

Engineering Applications/Pest Control Model

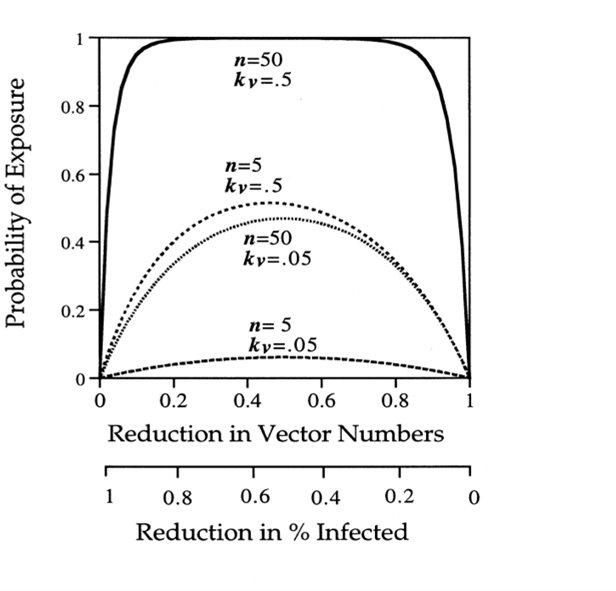
The control of pest populations is important not only from the perspective of maximizing crop yield, but also from the perspective of protecting human health. The USGS Patuxent Wildlife Research Center suggests the most effective strategy for vector-borne disease control is contingent on the limitation of human-pest interactions (Ginsberg, 2001). Equation 7, developed by Ginsberg (2001), is the simple model used to outline the probability that a person encounters the disease (P₁). It is easily seen that there are two methods of decreasing exposure probability: by decreasing k_v (the proportion of vectors carrying the disease), or by decreasing n (the number of interactions with pests). As seen in Figure 7, decreasing the n-value, i.e., using some method of pest control, is an effective method of reducing P₁ (Ginsberg, 2001).  

P_1 = 1-(1-k_v)^n \space\space\space\space\space (7)

However, the applications of pest-control can be equally harmful when we turn to synthetic chemicals, especially in the developing world where vector-borne diseases are most prevalent. These chemicals are so dangerous, in some places their adverse effects are disastrous, leading to more deaths than from infectious diseases themselves. When hazardous pesticides exist in an environment, people and other wildlife can be exposed to them through oral contact, ocular contact, dermal contact, or inhalation. Therefore, escaping their toxic effects is virtually impossible. Over time, the toxins aggregate in animal tissues, causing harm to not only that organism but all others that depend on them for sustenance (Kumar et al., 2012). Therefore, the implications of other sustainable pest-control methods are of the utmost importance.

Mathematical modeling and game theory can be applied to maximize mating-disruption efficiency through the release of sterile males into populations. While mating disruption is a powerful and effective substitute for pesticides, there have been cases of failure (Fitri et al., 2021). For example, in Brazil, mating disruption was introduced to control Leucoptera coffeella, commonly known as the coffee leaf miner. Their efforts, however, were ineffective and had no significant effect on the insects present or their harmful environmental effect (Ambrogi et al., 2006). Therefore, strategized targeting using a calculated model is of the utmost importance (Fitri et al., 2021). This is where game theory becomes useful. If the equilibrium point of the model is unstable, after the influx of sterile individuals, the population will return to its original state. To precipitate change in the population dynamics, there must be a shift away from homeostasis, and therefore a new stable equilibrium. In game theory, a stable equilibrium is defined as the point in which neither party would change their choices given the chance. If this equilibrium is not stable, the players will likely change their choice and the new population will not be permanent (Denoeux, 2012). By modeling the stability of the equilibrium points before the experiment begins, you can determine its efficacy.

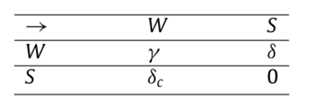
Using game theory for this situation, the game involves two “choices” for each female. She can either mate with the fertile male or the infertile male. Because this choice has a direct effect on her evolutionary fitness, she is in competition with the other females in the population. Figure 8 shows a matrix detailing the potential game theory outcomes of two females in competition for the fertile males (Flores, 2020). The W denotes a wild or fertile male, and the S denotes a sterile male. When both females chose W, there is a competition represented by γ. When the first player choses W, and the second player choses S, the offspring gained by player one is represented by δ. When the first player choses S and the second player choses W, the theoretical offspring entering the system are represented by δ_c. When both players chose S, the offspring entering the system is 0. For the equilibrium to be stable, the rate of competition must be less than the offspring entering the system (Eq. 8) (Flores, 2020). Otherwise, there would be no more mating with the sterile males and the population would return to its original rate.

\gamma < \delta_c + \delta \space\space\space\space\space (8)

The system of reaching this equilibrium can be outlined using the replicator equation, developed by Roca (2009) (Eq. 9). This gives us a model for the movement of the populations composure (x) for strategy (s). By taking the expected payoff for a specific strategy (given by the first term) and subtracting the average payoff (given by the second term), we get this model for state x. The application of this equation to our situation is given by equation 10 (Flores, 2020). This gives us a model for the population of sterile males over time. Figure 9 maps the population of fertile male medflies over time assuming that W + S = 1. It is seen that regardless of the initial population of fertile males, when δ_c is 0.4 offspring per day, the equilibrium point of around 0.22 is reached. This indicates the equilibrium point is stable, and with any disruptions the proportion of fertile males will return to around 22%. With the assumption that around 99% of an initial population would be fertile, this corresponds to a 77% decrease in the pest population (Flores, 2020).

\dot x_i = x_i [(Wx)_i - x^T Wx] \space\space\space\space\space (9)

\frac{dW}{dt} = W (1-W) (\delta - (\delta + \delta_c - \gamma)W) \space\space\space\space\space (10)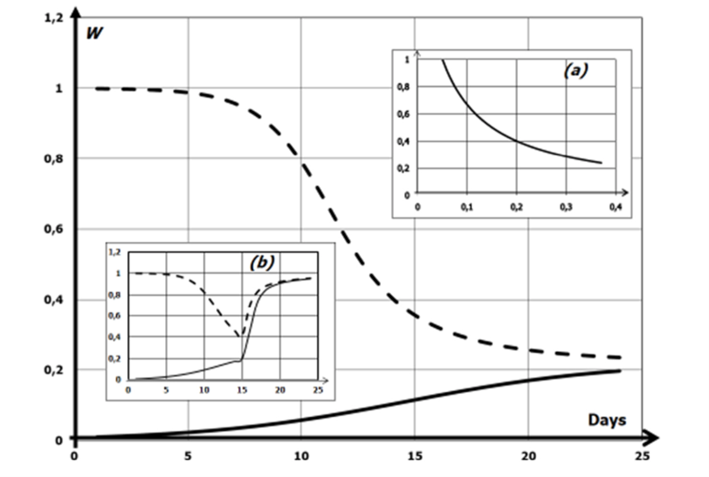

To become even more precise in our calculations, we must consider the diffusion of populations. This gives us a new equation, equation 11, where the area of land the population covers (a), the population density (w), and the rate of diffusion using a diffusion constant (D) are considered (Flores, 2020). When all these factors are considered, we can effectively determine the rate of influx of sterile males needed for to reach a stable equilibrium, and therefore effectively control pest populations. This saves time and money in applying a sustainable alternative to pesticides while still effectively addressing the global issue of vector-diseases and pest infestation.

\frac{\partial w}{\partial t} = w(1-wa)(\delta - (\delta + \delta_c - \gamma)wa) + D\nabla^2w(\overrightarrow{x},t) \space\space\space\space\space (11)

Conclusion

In this paper, we discussed the mathematics behind evolutionary game theory. Evolutionary game theory is a study where mathematical models are used to describe scenarios within biology. Evolutionary game theory will show which traits will best suit the individual in relation to its environment, all with the goal of promoting survival. These traits will eventually monopolize. An example of a mathematical model within evolutionary game theory is the G function framework. It is a set of differential equations that is used to model Darwinian dynamics. The goal of the G function framework is to describe population and strategy dynamics. Species use different strategies to evaluate the chance of mating. Females sometimes use coyness to evaluate a male’s probability of helping to raise the young. Mate choice can be explained through game theory with the standard sexual selection theory, where modelling will explain why a choice is favourable, even if at first it does not seem to be. The handicap principle is two models of phenotypic traits through additive and multiplicative models. An example of an additive model are deer antlers. A major application of evolutionary game theory within biology is pest control, where the proportion of vectors that carry disease and the number of interactions with pests are decreased to optimize yield. Although, pest control can be harmful if pushed too far, like with the use of chemicals. Evolutionary game theory offers a way for humans to model and predict outcomes in nature, which give us a deeper understanding of the world around us.

References

Ambrogi, B., Lima, E., & Sousa-Souto, L. (2006). Efficacy of mating disruption for control of the coffee leaf miner. BioAssay, 1.

Bijma, P. (2011). A general definition of the heritable variation that determines the potential of a population to respond to selection. Genetics, 189(4), 1347-1359. https://doi.org/10.1534/genetics.111.130617

Bukkuri, A., & Brown, J. S. (2021). Evolutionary Game Theory: Darwinian Dynamics and the G Function Approach. Games, 12(4), 72. https://www.mdpi.com/2073-4336/12/4/72

Bullock, S. (1999). Jumping to Bold Conclusions. Adaptive Behavior, 7(1), 129-134. https://doi.org/10.1177/105971239900700106

Caro, T. M. (1986). The functions of stotting in Thomson’s gazelles: some tests of the predictions. Animal Behaviour, 34(3), 663-684. https://doi.org/https://doi.org/10.1016/S0003-3472(86)80052-5

Denoeux, G. (2012). Stability in Mathematical Game Theory.

Discover Wildlife. (n.d.). Understanding the deer rut, plus the best places to see rutting red deer. BBC Wildlife Magazine. Retrieved November 25, 2021, from https://www.discoverwildlife.com/animal-facts/mammals/understand-the-british-deer-rut

Edward, D. (2014). The description of mate choice. Behavioral Ecology, 26, 301-310. https://doi.org/10.1093/beheco/aru142

Fitri, I. R., Bakhtiar, T., Hanum, F., & Kusnanto, A. (2021). The Characteristics and Optimal Implementation of Mating Disruption in Managing Pest Insect Population. Journal of Physics: Conference Series, 1863(1), 012001. https://doi.org/10.1088/1742-6596/1863/1/012001

Flores, J. C. (2020). Game theory approach to sterile release populations and replicator dynamics: Niche fragmentation and resilience. Physica A: Statistical Mechanics and its Applications, 551, 124212. https://doi.org/https://doi.org/10.1016/j.physa.2020.124212

Fromhage, L., McNamara, J. M., & Houston, A. I. (2008). A model for the evolutionary maintenance of monogyny in spiders. J Theor Biol, 250(3), 524-531. https://doi.org/10.1016/j.jtbi.2007.10.008

Ginsberg, H. S. (2001). Integrated pest management and allocation of control efforts for vector-borne diseases. J Vector Ecol, 26(1), 32-38.

Grinkov, V., Bauer, A., Gashkov, S., Sternberg, H., & Wink, M. (2018). Diversity of social-genetic relationships in the socially monogamous pied flycatcher (Ficedula hypoleuca) breeding in Western Siberia. PeerJ, 6. https://doi.org/10.7717/peerj.6059

Kaldari, R. (2009, May 16). File:Oxyopes salticus Kaldari 05 crop.jpg. Wikipedia. Retrieved November 25, 2021, from https://en.wikipedia.org/wiki/File:Oxyopes_salticus_Kaldari_05_crop.jpg

Kumar, N., Pathera, A., Saini, P., & Kumar, M. (2012). Harmful effects of pesticides on human health. Annals of Agri Bio Research, 17, 165-168.

Martin, Z. (2020, June 28). Advertising is a waste. And that’s kinda the point. Pigs Don’t Fly. https://pigsdontfly.com/2020/06/advertising-is-as-much-a-signal-as-a-message.html

Maynard Smith, J. (1984). Game theory and the evolution of behaviour. Behavioral and Brain Sciences, 7(1), 95-101. https://doi.org/10.1017/S0140525X00026327

McNamara, J. M., Fromhage, L., Barta, Z., & Houston, A. I. (2009). The optimal coyness game. Proceedings of the Royal Society B: Biological Sciences, 276(1658), 953-960. https://doi.org/doi:10.1098/rspb.2008.1273

Nur, N., & Hasson, O. (1984). Phenotypic plasticity and the handicap principle. Journal of Theoretical Biology, 110(2), 275-297. https://doi.org/https://doi.org/10.1016/S0022-5193(84)80059-4

Replicator dynamics. (n.d.). Systems Sciences, Innovation and Sustainability Research. Retrieved November 25, 2021, from http://systems-sciences.uni-graz.at/etextbook/gametheory/replicator.html

Roca, C. P., Cuesta, J. A., & Sánchez, A. (2009). Evolutionary game theory: Temporal and spatial effects beyond replicator dynamics. Physics of Life Reviews, 6(4), 208-249. https://doi.org/https://doi.org/10.1016/j.plrev.2009.08.001

Samuel Venner, Carlos Bernstein, Stéphane Dray, & Marie‐Claude Bel‐Venner. (2010). Make Love Not War: When Should Less Competitive Males Choose Low‐Quality but Defendable Females? The American Naturalist, 175(6), 650-661. https://doi.org/10.1086/652432

Wachtmeister, C.-A., & Enquist, M. (1999). The Evolution of Female Coyness – Trading Time for Information. Ethology, 105(11), 983-992. https://doi.org/https://doi.org/10.1046/j.1439-0310.1999.00487.x

Zahavi, A. (1975). Mate Selection-A Selection for a Handicap. Journal of Theoretical Biology, 53, 205-214. https://doi.org/10.1016/0022-5193(75)90111-3