Physical Analysis of Amoeba
Hailey Jukes, Adele Omichinski, Nicholas Da-Costa-Bastidas, Gil Qin
Abstract
Out of all the types of cell migration, amoeboid movement is studied very extensively due to its use by important biological components such as white blood cells. Despite the attention it has received, this type of cell movement has yet to be fully understood. Examining it from different perspectives helps researchers form a more comprehensive explanation of the physical processes driving the phenomenon. For instance, close analysis of the role of individual actin and myosin molecules based on our understanding of actomyosin networks in other eukaryotes reveals how subunit recycling and restructuring are integral to amoeboid locomotion. Study of the force-generating processes used by amoeba on a cell-wide scale, as well as of how these forces are transmitted to the substrate, helps explain how amoeba crawl on substrates to move. It is known that amoeba can move even without the presence of a substrate, a phenomenon known as amoeba “swimming.” This can only be understood by examination of fluid mechanics at a microscopic scale. Finally, pseudopods play a major role in all the types of movement just mentioned, so how these pseudopods form is also an area of interest discussed in this paper.
Introduction
Amoebas or amoeboid, constitute a diverse group of unicellular organisms, which have the unique ability to dynamically reshape their body through the extension and retraction of pseudopods, also commonly referred to as “false feet.” Despite their wide variety in size, morphology, and habitat, any organism that exhibits amoeboid movement is considered to be an amoeba. This mode of migration allows cells to move through various mediums without the need for external structures of motility such as flagella or cilia (Lämmermann & Sixt, 2009). This paper proposes a physical analysis of the current understanding of amoeboid movement, which is divided into four sections. In the first section, we explain the intracellular molecular forces that induce amoeboid movement. In particular, we discuss how polymerization and depolymerization of actin-myosin filaments are key forces driving amoeboid movement. We provide an overview of how the actin-myosin filaments create forces against the cell membrane to generate protrusions known as pseudopods. In the second section, we discuss the role that the hydrodynamics of the cytosol plays in amoeboid movement. We describe how contraction and relaxation of the actin-myosin filaments lead to cytosolic flow that consists of alternating regions of forward and backward flow. Importantly, despite the average speeds of forward and backward flow being equal, the time interval for the forward displacement is slightly longer and this difference is crucial for amoeboid movement. In the third section, we discuss the role that galvanotaxis plays in amoeboid movement. Galvanotaxis describes the reorientation of cells in locomotion upon exposure to a direct current electric field (dcEF). It is an important consideration since amoeboid cells respond in a highly sensitive fashion to electric stimuli. More specifically, amoebas exposed to a dcEF move unidirectionally towards the negatively charged cathode and this has been shown experimentally using an optical flow measurement technique known as micro-particle image velocimetry. In the fourth section, we will describe the different mechanisms by which amoeboids are able to generate movement. We explain why amoebas suspended in a fluid medium must propel forward using a different mechanism than when they are crawling on a solid substrate. When they are in a liquid medium, amoebas are unable to use attachment to gain traction and their ability to move is largely dominated by forces of viscosity. To move in a liquid medium, amoebas exert a constant force against their medium in order to propel forward and overcome the absence of inertia. We describe how amoebas are able to use dynamic shape changes and modified pseudopods to swim through fluid mediums.
The role of molecularly generated forces in amoeboid movements
As an amoeba is a single-celled eukaryote, the fundamental mechanics of its motility can be visualized theoretically at a molecular level. Amoeboid cytoskeletal components are theorized to generate and transmit various forces to direct movements of the amoeba, including the creation of pseudopodia along the leading edge of the cell, translocation of the back end of the cell, and even membrane invagination for endocytosis. Figure 1 illustrates the cycle of forces for amoeboid movement. The amoeba is able to use special design solutions built into its cytoskeleton to create the forces to carry out these processes. These design solutions also allow the amoeba to use a minimal amount of energy to generate force, as they harness energy from Brownian motion (random thermal fluctuations).
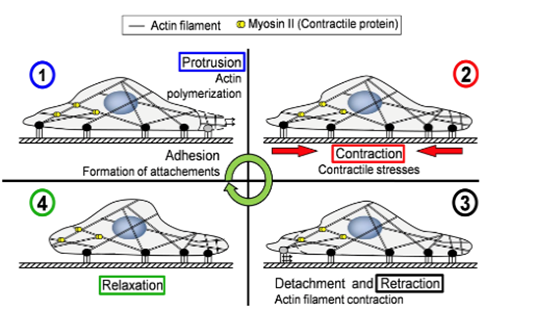
Figure 1: the motility stages of an amoeba (Alonso-Latorre et al., 2009).
The mechanism of actin treadmilling in amoeba membrane manipulation
The first stage of the amoeba's cellular motility cycle uses forces generated by the treadmilling of actin subunits to push out the cellular membrane along the leading edge of the cell. These primary membrane protrusions are called filopodia, and they are what the amoeba uses as its initial focal adhesions to its surface, driving forward locomotion (Álvarez-González et al., 2014).
Actin filaments perpendicular to the leading edge of the amoeba are in a constant state of polymerization at their free end; this means that they are in constant motion in the direction of the organism's movement. In addition to this, the back ends of the actin filaments are in a constant state of depolymerization occurring at the same rate, so the lengths of the actin filaments remain the same as they are translocating forwards. This allows the filaments to “grow” forward at a constant velocity; the continuous recycling of actin subunits means that the amoeba does not run out of subunits (Dembo 1989).
The cell membrane is constantly undergoing random thermal fluctuations; therefore, its position in space is always changing. These thermal fluctuations create a gap between the free end of the actin filaments and the cell membrane; the gaps allow actin monomers to slip in and polymerize onto the free end of the filament. The addition of a new actin monomer holds the membrane, which in this situation can be modeled as the load being pushed by the actin filament, at a position further outward than before.
The actin filaments can thus be modeled as a spring, as when the membrane (load) fluctuates “backward” into the actin filament, it is subjected to the restoring force of the filament and remains in its new position. The stiffness of the actin “springs” can vary depending on the amount of cross-linkage to other filaments. Cross-linkage between filaments occurs in the section of actin that exists before the free ends. This cross-linked section acts like a gel, and due to its structure, exhibits a nonlinear elasticity in the form of strain stiffening at medium strain levels. This means the elastic modulus of the actin network increases as the strain on it increases (Wen and Jamey, 2008). In addition, the actin polymer network shows strain-softening behavior at high levels of stress, causing the dissolution of the network under high strain.
More cross-linkage effectively functions as a set of springs in parallel, meaning that the “spring constant” of the actin filaments increases, making their restoring force stronger. The filaments are also stiffer if the length of their free end (the end that protrudes out from the crosslinked network and towards the cell membrane) is shorter; this also relates to their spring-like behavior as shorter springs tend to be less flexible (and vulnerable to deformation) than longer ones.
The frequency of the membrane's thermal fluctuations and the local concentration of actin subunits (for polymerization) determine the speed at which the membrane protrusions can grow (the polymerization velocity). This actin/cell membrane force mechanism can be visualized in Figure 2 (Yoshida and Soldati, 2006).
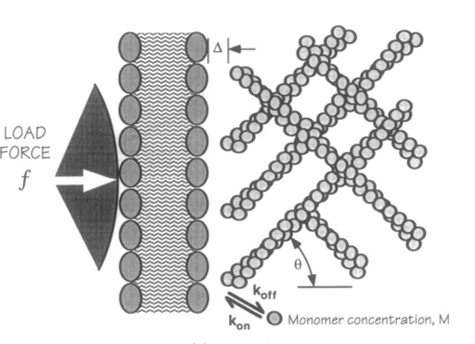
Figure 2: force mechanism between actin network and cell membrane for the creation of amoeboid membrane protrusions (pseudopod formation) (Yoshida and Soldati, 2006).
A filament exactly parallel to the amoeboid membrane cannot exert thrust on the membrane as the force it generates will be entirely perpendicular to the movement of the cell, thus performing no work. This then means that there is a particular optimal angle between filament and membrane that generates a maximal thrust force. The optimal angle depends on two factors: the load force, and the flexibility of the free end. Studies suggest that the optimal angle is an increasing function of load force and stiffness, also meaning a decreasing function of the free end length. Additionally, there is an inverse relationship between the load force and the polymerization velocity (Figure 3). Filaments growing at the optimal angle to the load predominate, as they will have the fastest polymerization velocity. A summary of cases for different optimal angles is shown in Figure 4 below.
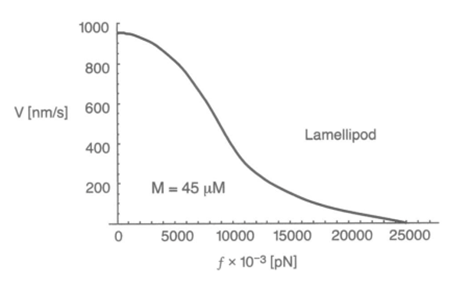
Figure 3: the inverse relationship between the velocity of Lamellipodia (membrane protrusion) formation from the actin network and the load force from the amoeba cell membrane (Mogilner and Oster, 1996).

Figure 4: optimal angle ranges for different load forces and actin filament flexibility in amoebae (Mogilner and Oster, 1996).
Cell membrane invagination for endocytotic events is governed by the same intracellular mechanical process. Actin filaments organize along the cell cortex at the site of phagocytosis, where they polymerize through the same mechanism as for pseudopod formation, but their specific angle and direction causes the polymerization force to invaginate the cell membrane and push a portion (which is to become the vesicle) inwards (see Figure 5).
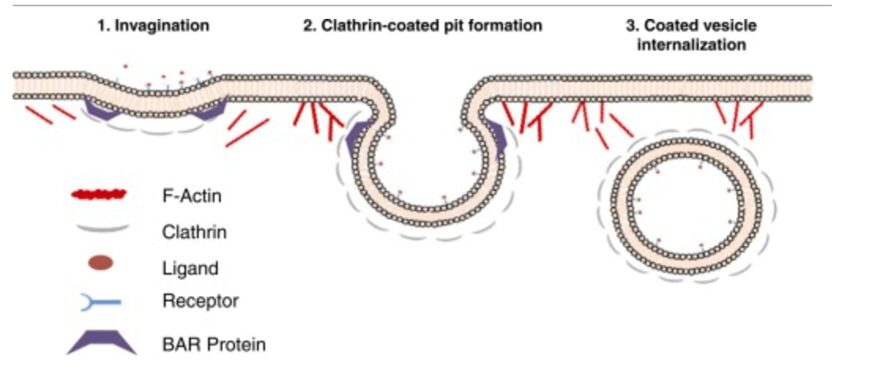
Figure 5: the role of actin in force generation for the internalization of endocytosing vesicles (Armstrong and Olsen, 2022).
Actomyosin contractility for back-end translocation of amoebae cells
In order to translocate the rest of its cell body in response to the protrusion of the leading edge, it is theorized that the amoeba uses contractive forces generated by an actomyosin network to complete its forward motion cycle. The exact process is not widely understood however it is hypothesized to work through myosin II contracting the actin cortex to generate force to retract the tail of the cell. Electron-microscopy reports show localization of thick filaments (myosin) restricted to areas of the amoeba that undergo retraction (Taylor et al., 1973). This process is visualized in Figure 6. Filamentous actin polymers act as a scaffold for myosin II motor proteins at the tail of the migrating amoeba. The myosin II fibers are interdigitated with long actin fibers and their multiple opposing motor domains use ATP hydrolysis to generate force to translocate along the actin filaments. This translocation causes a net contraction, which causes the actin filaments to be pulled towards each other (see Figure 7).
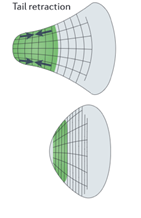
Figure 6: map of contractile forces at the back end (tail) of a migrating amoeba (Murrell et al., 2015).

Figure 7: direction of contractile forces within an actomyosin network (Murrell et al., 2015).
The contractile force transmission through actin is determined by the architecture of the filaments. The transmission success depends on filament length, density, and how well the filaments are crosslinked. Cross-linking is especially important as crosslinks proximal to the pointed end of the actin filament (the end that the myosin is translocating away from) cause the filament to experience tensile stress as opposed to compressive stress. Data shows that while actin fibers can buckle in response to as low as 1 pN of compressive force, they can withstand up to 300 pN of tensile stress. The design of the crosslinking is thus very important for the success of the compressive network. Recent studies also show that there is a necessity for some actin fiber deformation in order for the success of the contraction.
Myosin II uses chemical potential energy, which is stored in the bonds of ATP and released upon hydrolysis, to generate the force required to translocate itself along actin fibres. When ATP is bound to the myosin heads, it creates strain in the motor domains of the protein, which is stored energy. The hydrolysis of ATP releases the strain, allowing the myosin heads to perform a “power stroke” to return to their unstrained position, thus resulting in the movement of the protein along the filament.
Observing the activity of amoebae shows that the presence of myosin II is required to generate forces that spread along large sections of the cell membrane; in the absence of myosin, actin can only provoke localized forces, which are not enough to translocate the bulk of the cell body (Hsu et al., 2019). This supports the theory that an actomyosin network is required for the retraction of the amoeboid tail. Additionally, in mutated amoebae that lack myosin II the contraction part of the motility cycle is impaired. Therefore, it is hypothesized that amoebae may use an adapted variation of the sliding filament mechanism seen in sarcomeres of muscle cells in more complex eukaryotes for the translocation of their back ends (Fukui and Yumura 1986).
Hydrodynamics of amoeba cytosol
One explanation for how amoebas generate forces to create movement focuses on the hydrodynamics of the cytosol. It has been observed in various experiments that the flow of the liquid-like cell interior contributes to the forward movement of the amoeba (Matsumoto et al., 2008) (Lewis et al., 2015). In the studies discussed in the following two sections, the studied organisms were plasmodia of the species Physarum Polycephalum. These are organisms created by the combination of multiple cells into a large singular body containing many nuclei. These cells' large size facilitates the measurement of their displacement and physical properties and thus makes them ideal test subjects to study amoeboid movement.
Once the Physarum amoebae reach a critical size (measured to be approximately 100 µm lengthwise in one study and approximately 200-300 µm lengthwise in another), a rhythmic flow of cytosol from the posterior to the anterior end of the organism emerges. This pattern of flow is accompanied by a drastic increase in cell movement (Lewis et al., 2015). This flow of cytosol is driven by mechanical and osmotic pressures created by contraction and relaxation of the actomyosin network. These contractions serve to create a pressure gradient in the cell which drives the cytoplasmic flow. Just like the intracellular flow, the contractions also occur in a periodic manner and travel in the direction of cell migration. The contractile wave has the same period as the wave describing the flow of cytoplasm, with a phase shift of about a third of a period.
The flow of cytosol within the cell is characterized by alternating regions of forward flow and backwards flow which originate at the posterior end of the amoeba and travel in the direction of movement. The figure below illustrates measurements of the intracellular flow at different times. It is possible to note a progression from a region of forward flow spread throughout the entire amoeba, to a region of backward flow equally as spread out, to a moment of transition when the region of backward flow ends at the anterior end of the amoeba, and a new region of forward flow is just beginning to appear at the posterior end.

Figure 8: Instantaneous measures of intracellular flow measured in Physarum specimens at different times (Matsumoto et al., 2008).
The kymographs below (Figure 9) depict the flow within the amoeba over time and space. The alternating periods of forward and backward flow are easily visible, as represented by the orange and blue areas respectively.
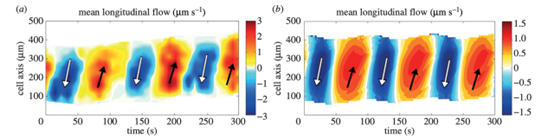
Figure 9: Kymographs of mean longitudinal flow (Lewis et al., 2015).
Matsumoto et al. (2008) also identify regions of contraction perpendicular to the cell axis, or the axis joining the anterior and posterior ends of the cell. These contractions are oriented either away from or toward the cell body, and they also propagate forward from the posterior end of the cell. These widthwise contractions correspond to contractions and relaxations of the actomyosin network described previously.
Hydrodynamic explanation of amoeba movement
The rhythmic flow of cytoplasm described above translates to an oscillating motion of fluid particles within the cell. These particles will undergo successive periods of forward and backward displacement. The term lf refers to the distance travelled forward by a fluid particle in the first half of a period, and lb refers to the distance travelled backward by that same single fluid particle in the second half of the period. The center of gravity of the cell also oscillates in this fashion as a consequence of the shifting flows, and the cell's forward and backward displacements are labelled Cf and Cb respectively.
For the amoeba to exhibit a net forward displacement, the ratio Cf/Cb must be greater than 1. This is made possible by a measured asymmetry in the cytoplasmic flow wave. In fact, although the average speeds of forward and backward flow are equal, the time interval during which the cytoplasm undergoes forward displacement is slightly longer than that during which it undergoes backward displacement, corresponding to a bit more than half the period. This contributes to the forward translation of fluid particles over several flow periods. The kymographs above make this apparent, as the width of the orange bands representing forward flow is slightly larger than the blue ones.
This asymmetry is well recognized in the literature. However, the relative importance of this asymmetry in explaining amoeboid movement is debated. To quantify this relationship, researchers examined estimated displacements lf and lb of a virtual cytoplasm fluid particle and the consequent ratio of forward displacement lf/lb. This ratio was then compared to the experimentally measured ratio Cf/Cb describing the displacement of the center of gravity of Physarum cells (Matsumoto et al., 2008). If the ratios were identical or very similar, this would justify flow shift asymmetry being the main determinant of cell displacement.
Using the average flow velocity, the length of a period of forward and backward flow, and the speed with which the region of forward or backward flow travelled along the cell axis, researchers were able to estimate the ratio lf/lb corresponding to several Physarum cells under study, for which they also measured the ratio Cf/Cb. By plotting one of these ratios as a function of the other in the graph below, the researchers concluded the center of all the data points was close enough to the diagonal representing perfect equality between both ratios to claim that the shifting cytoplasmic flow was the main driver of the amoebae's movement.
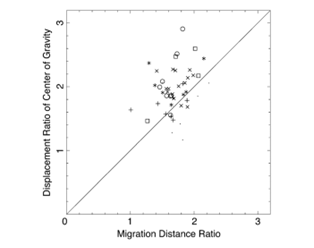
Figure 10: Ratio of displacement of the center of gravity Cf/Cb plotted against the ratio of migration distances of forward and backward flow lf/lb) (Matsumoto et al., 2008).
Considering cell-substrate adhesion as an important factor for movement
In a more recent study, other researchers reproduced the experiment described above, measuring the ratios lf/lb and Cf/Cb for a new batch of Physarum plasmodia with a similar methodology to that presented above (Lewis et al., 2015). Their results are presented in the following graph.
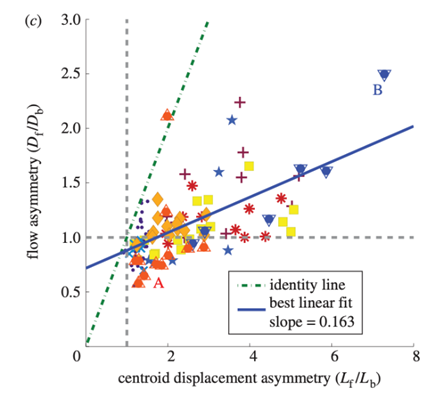
Figure 11: Ratio of migration distances of forward and backward flow lf/lb plotted against the ratio of displacement of the center of gravity Cf/Cb (Lewis et al., 2015).
Their results tell quite a different story. Instead of measuring the center of their data points, they plotted a line of best fit, represented in blue above. The slope of this line is markedly different from that of what they call the “identity line” in their graph, the line representing equality between the ratios. Furthermore, the researchers remark that some data points have an lf/lb ratio of less than one, which would suggest the amoeba should actually move backward, yet experimental data shows a forward displacement of their center of mass.
An aspect of amoeboid movement that is disregarded by the hydrodynamic explanation of amoeboid movement is the adhesion between the cell and the substrate. This is relevant when considering amoeba crawling as opposed to other means of locomotion such as swimming. The exact mechanism by which amoeba stick to the substrate is still unknown. In building a mathematical model to represent amoeba movement, Lewis et al. represent the adhesion mechanism by a viscous drag law, of the form:
![]()
in which the coefficient in front of the velocity U is represented by the following wave equation
![]()
In simpler terms, this describes how coordinated cell-substrate adhesion is modulated through space and time. A represents the strength of coordinated adhesion, and ɛ represents non-coordinated cell-substrate adhesive interactions.
This equation is only a part of the mathematical model used by the researchers. The model also incorporates a variety of other forces exerted upon different parts of the cell, as well as another wave equation describing the contractile wave discussed earlier. After running some simulations, the researchers established that overall, the model represented amoeba movement accurately.
They were then able to use this model to try and predict the effect on amoeba movement of the coordination between cell adhesion and actomyosin contraction, or lack thereof. Their first conclusion was that coordinated adhesion is indeed critical to cell movement, as amoebae modelled with A = 0 failed to migrate, despite having a significant ɛ. This means passive, uncoordinated adhesion is not enough to produce movement. Moreover, comparing different phase shifts between the contraction wave and the adhesion modulation wave revealed that a phase shift of about 3π/2 was ideal for maximizing migration speed. Simulations taken with other phase shifts resulted in slower speeds or even amoeba moving backward instead of forwards.
Knowing these results are based on model simulations may make them seem a bit farfetched, but the near equivalence of the predictions made by the model and the behavior of real-life amoeba serves to support the credibility of the model. At the end of the day, all models have fallacies, and indeed the objective of a model is usually not to represent reality perfectly. It is rather to simplify certain aspects of reality so that we may better study them and deepen our understanding of the real world. In this case, the simulations reveal that cell-substrate adhesion plays a non-negligible role in amoeboid movement and that the coordination of adhesion and contraction-driven cytoplasmic flow is a key factor in shaping the displacement of the cell.
Galvanotaxis and the interpretation of amoeboid locomotion mechanism using micro particle image velocimetry
Galvanotaxis describes the reorientation of cells in locomotion upon exposure to direct current electric fields (dcEF). The galvanotactic phenomenon has been repeatedly observed in research studies and applied to the analysis of cytoplasmic streaming and the interpretation of movement mechanisms of amoeboid cells. The history of researching the galvanotactic behaviors of protozoan cells dates back to 1889 when German physiologist Max Verworn recorded his observation of the redirection of the movement of amoeboid cells toward the cathode when exposed to dcEF. In the absence of an electric field, the natural movement of amoeba is characterized by low vigor and randomness in orientation, as well as the simultaneous protrusion of multiple pseudopodia in multiple directions (Alt et al., 2012). However, by exposing amoeba to dcEF, amoeba is stimulated to move unidirectionally towards the negatively charged cathode in an organized fashion. Therefore, through exposing the amoeba to dcEF, the movement mechanism of the organism can be further studied (Figure 12).

Figure 12: Comparing the cell shape, pseudopodia protrusion, and direction of movement of an amoeba exposed to dcEF (a) and of a free-moving amoeba without exposure to dcEF (b) (Alt et al., 2012).
Furthermore, the higher rate of movement of amoeba at 1-2 µm/s, compared to other tissue cells, offers the possibility of quantitative measurement of the directed locomotion of amoeboid cells with more simplicity (Korohoda et al., 2000). Amoeboid cells are also capable of long-term migration towards the cathode for up to several hours. Experiments performed by Korohoda et al. demonstrate that amoeboid cells, in a highly sensitive manner, respond to electric stimuli by immediate restriction of anode-directed pseudopodia extension followed by the induced protrusion of cathode-directed pseudopodia.
The field strength (E) of an experimental amoeba chamber can be estimated by the formula E = I / σA, where I is the current in Amperes (A), σ represents the medium conductivity in Siemens per centimeter (Scm-1), and A denotes the cross-sectional area of the chamber in cm2. As a result, through manipulating the intensity of the current, the corresponding electric field strength can be determined by the above principle.
As the strength of dcEF increases, amoeboid movement is characterized by less frequent formation of lateral pseudopodia and more frequent initiation of pseudopodia in the cathode-facing anterior. This is evident in Table 1 as the high percent of new pseudopodia formation in segment I of the cell when subject to a stronger dcEF (Figure 13). In contrast, in the absence of dcEF, the amoeba exhibits a higher frequency of pseudopodia formation in sections II, III, and IV than when it is exposed to an electric field. This is because, without an imposed electric stimulus orienting the amoeba towards the direction of motion, the probability of any particular direction of migration for an amoeba is equal. Consequently, at a field strength of 0, pseudopodia protrusion initiates in the lateral and rear region of the amoeboid cell at a higher frequency compared to when it is subject to dcEF (Table 1). The same phenomenon is observed in the microscopic image of migrating amoeba in Figure 14. In the absence of electric stimuli, the shape of amoeboid cells is more irregularly configured, with randomly scattered events of pseudopodia protrusions. In comparison, when exposed to an electric field, the shape of amoeboid cells becomes more organized and uniform, and a strong tendency of pseudopodia formation along the direction of the electric field can be observed.
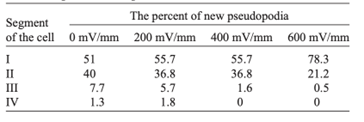
Table 1: Percent of new pseudopodia formation in different segments of the amoeba as a response to different electric field strengths, ranging from 0 to 600 mV/mm (Korohoda et al., 2000).
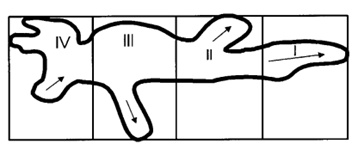
Figure 13: To measure the percentage of new pseudopodia development in different regions of the cell, the amoeba is divided into four segments where section I is the anterior region of the cell and IV represents the uroid or the posterior region of the cell. The direction of pseudopodium extension or retraction is indicated by arrows (Korohoda et al., 2000).
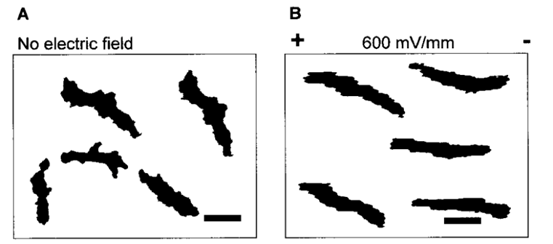
Figure 14: Comparing the shape of amoeba in the absence of electric field (A) and subject to an imposed dcEF of a field strength of 600 mV/mm (B) with the negatively charged cathode positioned on the right of the diagram (Korohoda et al., 2000).
Given the galvanotactic behavior of amoeba, to analyze cytoplasmic streaming and amoeba movement, Alt et al. applied an optical flow measurement technique – micro-particle image velocimetry – to measure the intracellular fluid velocity of a cathode-oriented amoeba in motion, using amoeba organelles as tracer particles. The objective of the investigation was to examine the hydrodynamic explanation of amoeba locomotion – how intracellular flow in amoeba is responsible for cell motility. Using particle image velocimetry, a 2D plot of fluid velocity vectors of a complete amoeboid cell in motion under dcEF is constructed, along with a number of velocity profiles for different cross-sections of the amoeba (Figures 15 and 16).
By comparing the cross-sectional velocity profiles of the front section of the amoeba (Figure 16 a and b) with the cross-sectional velocity profiles of the rear section (Figure 16 e and f), it is observed that the velocity of cytoplasmic flow of the rear part of an amoeba is only half as high as the velocity in the front region. The significantly higher fluid velocity detected in the front part of the amoeba corresponds to the higher frequency of pseudopodia development associated with the anterior of the cell and is a strong reflection of the pumping mechanism of the amoeba cytoplasm based on spontaneous gel-sol conversion. According to the sol-gel theory of amoeba locomotion, to initiate the development of pseudopodia, the anterior end of the amoeba undergoes a local and partial liquefaction of the plasmagel, driving the central plasmasol forward to enter the newly developed pseudopodia (Masaki et al., 2005). Concurrently, the outer viscoelastic plasmagel along the lateral and rearward boundaries contracts to force the streaming of plasmasol from the rear to the front. Therefore, the localized contractions that occur at the rear of the cell – caused by a system of contractile proteins, namely, actin and myosin – result in a localized increase in hydrostatic pressure in the posterior of the cytoplasm, ultimately contributing to a lower velocity at the rear.
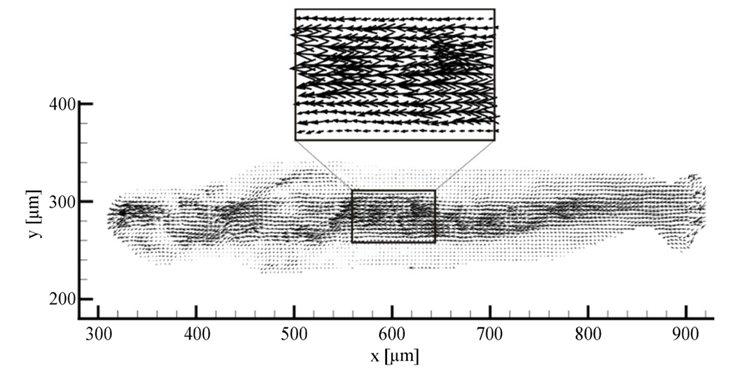
Figure 15. 2D plot of vectors of the fluid velocity field of a crawling amoeba (Alt et al., 2012).
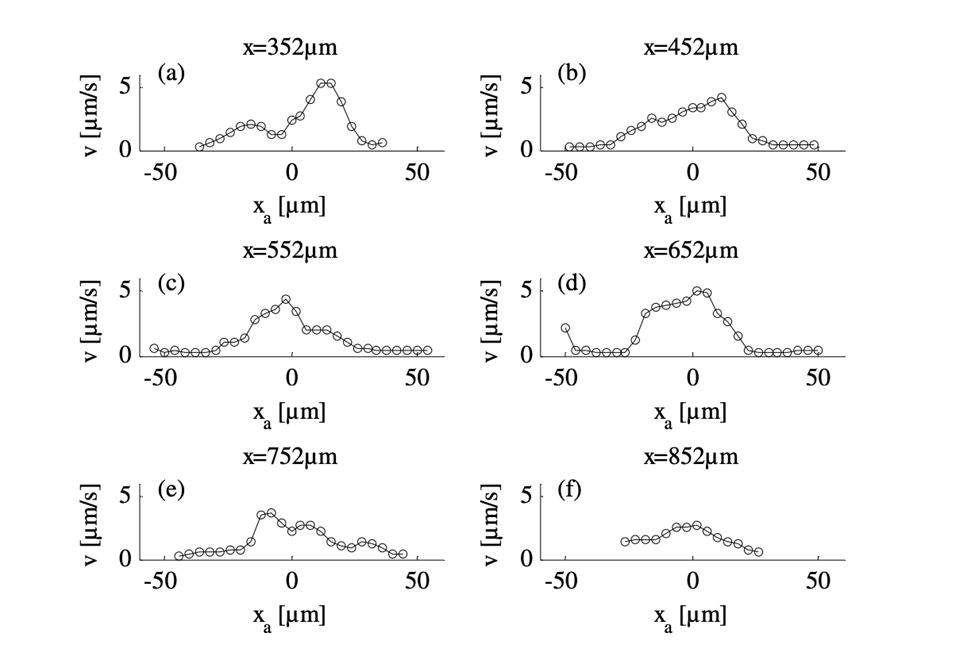
Figure 16: Velocity profiles demonstrating the differences in velocities for six cross-sections of the amoeba from an x-position of 352 µm (a) to 852 µm (f) with 352 µm at the front section of the cathode-directed amoeba in motion and 852 µm at the rear section of the amoeba. The x-positions of the cross-sections are calibrated and interpreted with reference to the x-axis of Figure 15 (Alt et al., 2012).
In another particle image velocimetry study of amoeba locomotion conducted by Matsumoto et al., by producing a series of velocity fields of cytoplasm streaming, the researchers studied the differences in width changes and local contractile activity that occur in different regions of the amoeba (Figure 17). In this study, an important spatiotemporal trend of protoplasmic streaming was observed.
In Figure 17, from 290 s to 306 s, thinning in the width of the tail end begins while the anterior of the amoeba still displays thickening in shape, depicted by a pair of opposite and equal solid arrows oriented away from the amoeba. However, from 306 s to 322 s, as the decrease of tail width progresses, the thinning of the cell shape commences its propagation to the anterior. This is demonstrated by the emergence of opposite pairs of solid arrows directed toward the amoeba in the central and anterior regions of the cell, denoting a decrease in cell width in the corresponding regions. At 338 s, the anterior and central regions of the cell still exhibit a decreasing trend in cell width, whereas a thickening tendency of cell width originates at the tail. From 354 s to 370 s, the propagation of thickening progresses to the anterior. Variations in the direction of cytoplasmic streaming follow a similar pattern as changes in cell width. At 290 s, forward flow, denoted by open arrows, is only evident in the rear region. The forward flow of plasmasol then propagates to the middle region at 306 s and to the anterior region at 322 s. Similarly, at 338 s, a backward direction of flow emerges in the tail and propagates to the middle and anterior from 354 s to 370 s. Therefore, the experiment demonstrates that the contraction of actomyosin, the resulting streaming of plasmasol, and the relaxation of actomyosin unanimously originated from the posterior and emanated to the anterior. Contraction and relaxation in the actomyosin system are represented as the reduction and expansion of cell width, respectively. This finding coincides with the sol-gel theory of amoeboid movement mechanism, where local contractile activity is hypothesized to commence in the posterior to facilitate cytoplasmic streaming in the direction of motion.
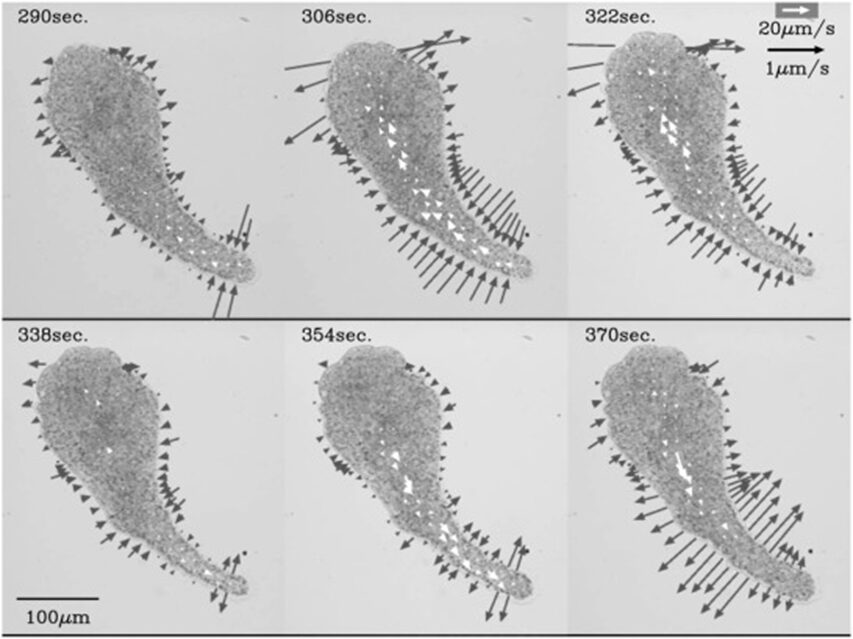
Figure 17: A series of velocity vector fields (open arrows) and rate of width changes (solid arrows). A pair of opposite solid arrows of equal length are drawn perpendicular to the longitudinal axis to depict width changes in the amoeba (Matsumoto et al., 2008).
Amoeboid swimming: amoebas in fluid suspension
In conventional experimental investigations of amoeboid movement, cells are studied when crawling over a solid substrate. However, researchers have more recently become interested in exploring the mechanism through which amoebas suspended in a fluid medium use pseudopods and dynamic shape changes to achieve forward propulsion (Barry and Bretscher, 2010).
The hypothesis regarding amoeboid swimming arose from the study of a mutant strain of Dictyostelium discoideum, lacking the gene for the SadA protein. SadA is an adhesion receptor that was shown to play an important role in cell-substrate adhesion. In fact, sadA-null cells grown in a Petri dish were unable to attach to the substrate and only settled on the surface of the dish due to gravity. An experiment also showed that 70 % of wild-type cells could maintain attachment under shaking conditions (50 revolutions per minute/rpm), whereas sadA-null cells were incapable of initiating attachment, even without shaking (0 rpm) (Figure 18).
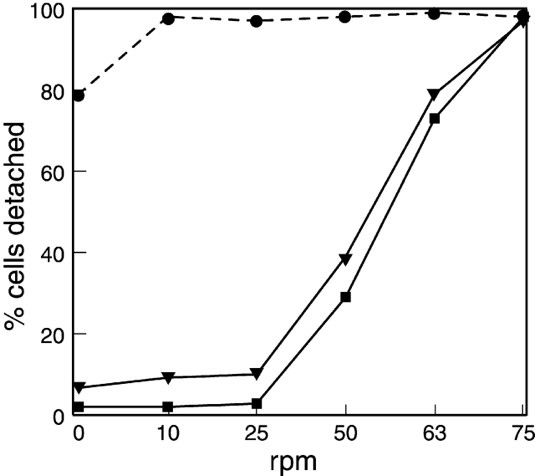
Figure 18: Graph comparing the percentage of cells detached from the surface of the Petri dish at different rates of shaking (revolutions per minute) for sadA-null cells (closed circles), the wild-type cells (closed square), and sadA-GFP rescued cells (inverted triangles; not discussed in this paper) (Fey et al., 2002).
This suggested that the absence of the SadA protein results in a complete inability of cells to attach to a substrate. However, when observing the motility of sadA null cells, they appeared to migrate normally and even covered larger distances than wild-type cells. The vegetative wild-type cells exhibited an average instantaneous velocity of 3.2 µm/min, whereas the mutant cells displayed nearly double the velocity, reaching 6.3 µm/min (Figure 19). This observation suggested that sadA-mediated adhesions in wild-type cells actually hinder or restrain cell movement (Fey et al., 2002).
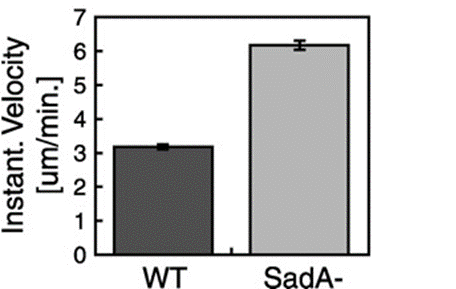
Figure 19: Bar graph comparing the instantaneous velocities (in m/min) of wild-type (WT) and sadA null cells (SadA-) grown in the vegetative state (Fey et al., 2002)
Comparable findings were also observed in a study examining the motility of mutant Dictyostelium discoideum cells deficient for the GTP-binding protein Rap 1. Similarly, to SadA, Rap 1 significantly contributes to adhesion between Dictyostelium cells and the surrounding substrate. In gbpD-null cells, which lack the cofactor GBP required for Rap 1 activity, pseudopods were observed to form at a rate and speed almost identical to wild-type cells. However, the pseudopods in gbpD-null cells grew longer and larger, resulting in enhanced migration speed. This implies that cells with adhesion defects can still utilize pseudopods for migration, and once again strong adhesion slows down movement. Rather than crawling on the substrate by forming attachments, adhesion-defective mutant cells will glide over the substrate (Van Haastert, 2001).
The gliding behavior observed in amoeboid cells with adhesion defects prompted researchers Barry and Bretscher at the MRC Laboratory of Molecular Biology to explore whether Dictyostelium discoideum amoeba rely on a substrate for movement or if they have the ability to swim. They concluded that amoebas could swim and do so by a mechanism that appears to be very similar to amoeboid crawling. This is because, in both swimming and crawling, amoeboid movement follows a common pattern. Cells start by extending a lamella or lobe and occasionally they even form microspikes. When the leading-edge splits, one of the lobes retracts and moves backward towards the rear of the cell along with other surface projections. These changes in cell shape produce forward momentum of the cell body (Figure 20). Additionally, when comparing swimming and crawling, cells displayed very similar migration speeds and, in both situations, cells responded to chemotactic agents in their environment (Barry and Bretscher, 2010).
Figure 20: A series of images taken in 10-second intervals showing the different shapes of a swimming amoeba in fluid suspension. (Barry and Bretscher, 2010).
Despite the observed similarities between swimming and crawling in amoebas, it is still unclear how these cells can move when suspended in a fluid medium if they are unable to gain traction with their environment. In the context of cell movement on a surface-attached substrate, the accumulation of F-actin at the front of the cell helps push the cell forward. This is because when cells are crawling, they temporarily anchor these F-actin filaments to the substrate in order to gain traction and propel forward. However, this mechanism cannot work for cells swimming in a fluid medium since they cannot attach to the medium. The front of the cell would move forward while the rear simultaneously moves backward, and the overall position of the cell would not change.
Purcell's scallop theorem
“The Scallop theorem” is a fundamental physics concept that is essential when describing the locomotive mechanism of various microorganisms in fluid environments. The theorem was formulated by Edward Purcell in his 1977 paper “Life at Low Reynolds Number”. In his paper, Purcell explored the physics of tiny organisms, such as bacteria and sperm cells, and how they are able to move in fluids. He noted that microorganisms swimming in low Reynolds number environments are predominantly subjected to viscous forces and are not affected by the forces of inertia (Purcell, 1976). This theorem is relevant when studying ameboid swimming since it can partly explain their behavior and motility in fluid suspension. Although different species of amoeba can vary greatly in size, from as small as 2.3 to 3 µm (as seen in the marine amoeba Massisteria voersi in Figure 21) (Mylnikov et al., 2015), to as large as 20 cm (as seen in deep-sea Xenophyophores (Figure 22)) (Gooday et al., 2017), most free-living freshwater and marine amoeba are of the microscopic scale. Therefore, like the bacteria and other microorganisms studied by Purcell, amoebas swim in low Reynolds number environments.
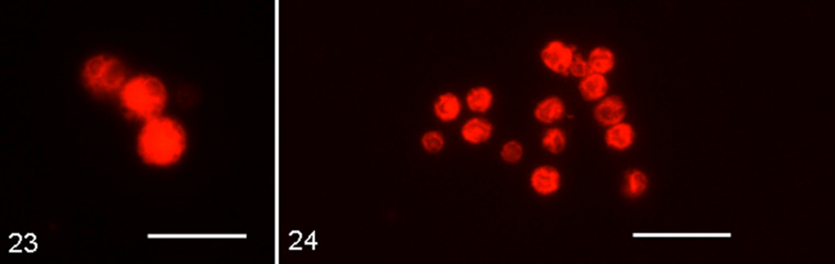
Figure 21: Epifluorescence Micrographs of Massisteria voersi (Scale bar: 10 mm) ( (Mylnikov et al., 2015) .

Figure 22: Image of a large 20 cm wide Xenophyophore (NOOA, 2010).
The Reynolds number (Re) is a dimensionless parameter used in fluid mechanics to describe the flow structure of a fluid around an object. The Reynolds number for a fluid medium is determined by the ratio of inertial forces (Fi) over viscous forces (Fv) (Rapp, 2017).
![]()
When the Reynolds number is high, the inertial forces prevail and bodies in motion tend to stay in motion. In contrast, when the Reynolds number is low, viscous forces prevail and objects tend to resist momentum. In other words, at a low Reynolds number, how an object is moving at a given moment is entirely determined by the forces that are exerted on the object at that moment, and by no other prior forces.
The Reynolds number can also be described as the product of fluid density (ρ), the velocity (V), and the length of the body (L) divided by the dynamic viscosity of the fluid (µ):
![]()
This formula shows why humans and most other animals with relatively large dimensions (large value of L), operate at a high Reynolds number, whereas microorganisms (small value of L), including amoebas, operate at a low Reynolds number (Lauga, 2007). Even relatively small animals like fish are classified as macroscopic swimmers and they swim at high Reynolds number (Re » 100) where inertia dominates. In comparison, bacteria are classified as microscale swimmers, and they swim at low Reynolds number (Re » 10-4) where viscosity dominates (Figure 23) (Bastos-Arrieta et al., 2018).
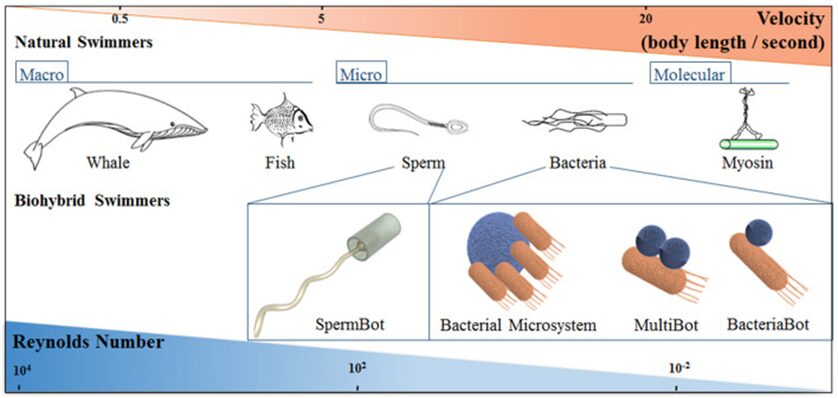
Figure 23: Schematic correlation between length scale and Reynolds number in swimmers of various sizes (Bastos-Arrieta et al., 2018).
When a body undergoes periodic changes in a setting without inertia (low Reynolds number), if the sequence of shapes it exhibits while moving forward is the same as when it moves in reverse (a condition known as reciprocal motion), then the body's resulting position will remain constant over one complete period of motion. In the case of amoebas, this explains why the reciprocal protrusion and retraction of pseudopods are insufficient for creating forward momentum. To further prove his theorem, Purcell used scallops as an example. Normally, these organisms operate in a high Reynolds number environment and are able to propel themselves forward by a reciprocal movement. They open their shell very slowly and close them very fast, which causes water to squirt out and their body to move forward due to inertia. However, if this same mechanism were applied at a low Reynolds number environment, in the absence of inertia, the scallop would not be able to swim because it only has one hinge. No matter how fast or how slow the scallop would open or close its shell, it will always have only one degree of freedom, and therefore the motion would always be reciprocal. This means that micro swimmers need to change their shape in a non-reciprocal fashion to enable a distinct temporal direction to their motion, which naturally results in the creation of wave-like deformations (Lauga, 2011).
Mechanisms of swimming for microorganisms (as proposed by Purcell)
To achieve forward movement at a low Reynolds number, cells need to displace the surrounding medium in the opposite direction in order to shift their own center of gravity. In his study, Purcell examined three methods by which micro swimmers can achieve this form of locomotion (Figure 24).
Rotation screw
Certain microorganisms employ a rotary, screw-like motion to push the surrounding medium in one direction, propelling themselves forward. For example, some types of bacteria have multiple flagella that cluster together and move synchronously, generating helical waves in screw-like motions. Since amoebas do not have flagella, this first mechanism cannot serve to explain the mechanism of amoeboid swimming (Berg and Anderson, 1973).
Asymmetrical shape changes
Other microorganisms achieve locomotion through asymmetrical shape changes, moving structures like cilia in a breaststroke-like motion to move the medium in the opposite direction. For example, when cilia form a “carpet” on a cell's surface, they move together with a constant phase difference, creating a metachronal wave-like pattern at their tips (Rode et al., 2021). This movement pattern enables directed motion in low Reynolds number environments, since the beats of the cilia, when combined together, are non-reciprocal. Since pseudopodal extensions move in a backward direction instead of bending around a fixed point, this second mechanism could not entirely describe amoeboid swimming (Gueron et al., 1997).
Toroidal cell with rotating surface
Lastly, some microorganisms may adopt a toroidal or doughnut-shaped structure with a surface that is capable of rotating. As the surface rotates, it interacts with the surrounding medium which effectively drags it backwards in the opposite direction of the movement. This action creates a propulsive force that drives the cell forward. With slight modifications, this third mechanism is the closest to the one used by amoebas to move in fluid suspension (Barry and Bretscher, 2010).
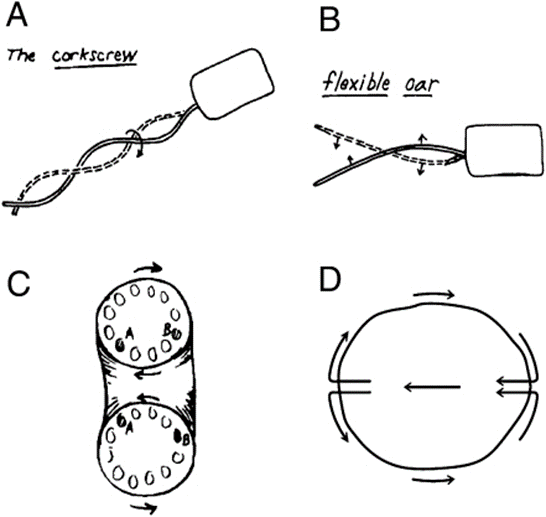
Figure 24: Schematic drawing of the three different swimming mechanisms for microorganisms as proposed by Purcell. They include the rotation screw (A-The corkscrew), the asymmetrical shape changes (B–Flexible oar), and the toroidal cell with rotating surface (C–D) (Barry and Bretscher, 2010).
Amoeboid swimming model: modified third mechanism.
A group of researchers from Joseph Fourier University succeeded in developing a simplified model to represent the swimming mechanism of amoebas in fluid suspension. This model describes amoeboid swimming as being primarily determined by the sequence of shapes the amoebas adopt. These deformations generate forces against the surrounding liquid, effectively propelling the amoeba forward in the fluid. The speed of movement does not play a significant role in amoeboid swimming, it is rather the dynamic alteration of shape that drives propulsion (Farutin et al., 2013). Furthermore, a study by Peter J.M. Van Haastrert at Groningen University showed that when amoebas swim, they extend smaller pseudopods compared to when they walk on a solid substrate. After they extend forward, these small pseudopods transform into rearward-moving lateral bumps, which remain stationary relative to the substrate around them, thereby serving as paddles that help assist the cell in its forward propulsion (Figure 25) (Van Haastert, 2001).
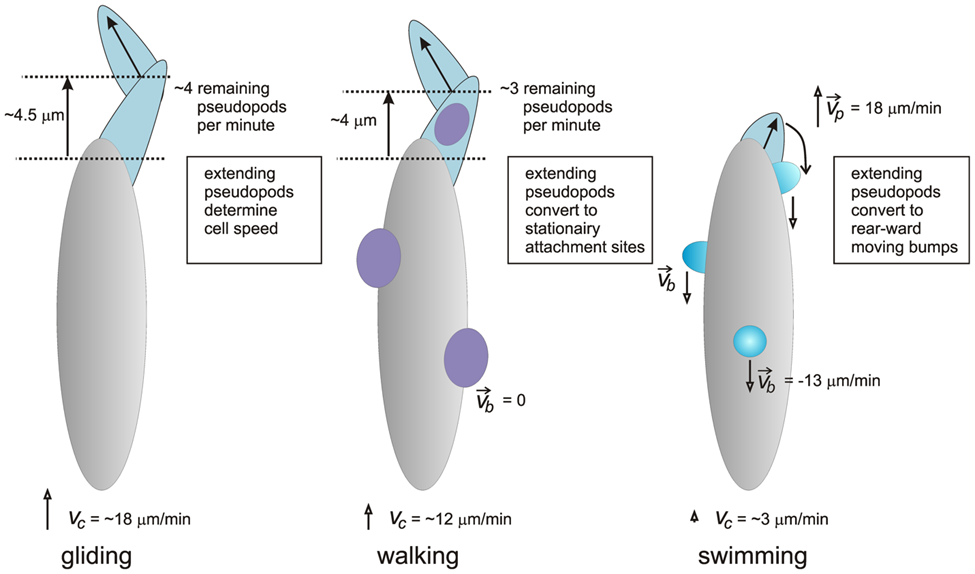
Figure 25: Schematic model depicting the different mechanisms of pseudopod extension in gliding (left), walking (center), and swimming (right) amoeba (Van Haastert, 2001).
Conclusion
The amoeba is a single-celled eukaryote, that employs both microscopic and macroscopic physical design solutions via interactions with its environment. These design solutions allow the amoeba to make its life processes more efficient. For example, we have looked at the applications of these design solutions for amoeboid locomotion, which is a form of movement specialized to amoeboid organisms. Amoeboid movement allows amoeba cells to translate forces from a molecular origin, into ones that power the movement of the entire cell, Additionally, the amoeba is able to generate movement using random thermal fluctuations- an energy source that is often unusable for metabolic processes. Physical theory is very present in the ways that amoebae move, both within how the movement is generated, and in the characteristics and analysis of the movement. This can be seen in the ways the amoeboid movement changes based on the environment the organism is in to be most efficient- the changes can be based on the physical characteristics of the environment, or due to other forms of stimuli. Through this exploration, it is clear that amoebae have incorporated physics into the ways they exist and persist in spaces allowing them to optimize their methods for survival.
References
Armstrong, G., & Olson, M. F. (2022). Bending over backwards: BAR proteins and the actin cytoskeleton in mammalian receptor-mediated endocytosis. European Journal of Cell Biology, 101(3), 151257. https://doi.org/https://doi.org/10.1016/j.ejcb.2022.151257
Alonso-Latorre, B., Meili, R., Bastounis, E., Del Alamo, J. C., Firtel, R., & Lasheras, J. C.. (2009). Distribution of traction forces associated with shape changes during amoeboid cell migration. https://doi.org/10.1109/iembs.2009.5333191
Alt, W., Böhm, V., Kaufhold, T., Lobutova, E., Resagk, C., Voges, D., & Zimmermann, K. (2012). Theoretical and Experimental Investigations of Amoeboid Movement and First Steps of Technical Realisation. In C. Tropea & H. Bleckmann (Eds.), Nature-Inspired Fluid Mechanics: Results of the DFG Priority Programme 1207 ”Nature-inspired Fluid Mechanics” 2006-2012 (pp. 3-23). Springer Berlin Heidelberg. https://doi.org/10.1007/978-3-642-28302-4_1
Álvarez-González, B., Bastounis, E., Meili, R., Del Álamo, J. C., Firtel, R., & Lasheras, J. C.. (2014). Cytoskeletal Mechanics Regulating Amoeboid Cell Locomotion. Applied Mechanics Reviews, 66(5), 050804. https://doi.org/10.1115/1.4026249
Barry, N. P., & Bretscher, M. S. (2010). Dictyostelium amoebae and neutrophils can swim. Proceedings of the National Academy of Sciences of the United States of America, 107(25), 11376–11380. https://doi.org/10.1073/pnas.1006327107
Bastos-Arrieta, J., Revilla-Guarinos, A., Uspal, W. E., & Simmchen, J. (2018). Bacterial Biohybrid Microswimmers. Front Robot AI, 5, 97. https://doi.org/10.3389/frobt.2018.00097
Berg, H. C., & Anderson, R. A. (1973). Bacteria Swim by Rotating their Flagellar Filaments. Nature, 245(5425), 380-382. https://doi.org/10.1038/245380a0
Dembo M. (1989). Mechanics and control of the cytoskeleton in Amoeba proteus. Biophysical journal, 55(6), 1053–1080. https://doi.org/10.1016/S0006-3495(89)82904-2
Fey, P., Stephens, S., Titus, M. A., & Chisholm, R. L. (2002). SadA, a novel adhesion receptor in Dictyostelium. The Journal of cell biology, 159(6), 1109–1119. https://doi.org/10.1083/jcb.200206067
Fukui, Y. and Yumura, S. (1986), Actomyosin dynamics in chemotactic amoeboid movement of Dictyostelium. Cell Motil. Cytoskeleton, 6: 662-673. https://doi.org/10.1002/cm.970060614
Farutin, A., Rafaï, S., Dysthe, D. K., Duperray, A., Peyla, P., & Misbah, C. (2013). Amoeboid swimming: a generic self-propulsion of cells in fluids by means of membrane deformations. Physical review letters, 111(22), 228102. https://doi.org/10.1103/PhysRevLett.111.228102
Gooday, A. J., Aranda da Silva, A., & Pawlowski, J. (2011). Xenophyophores (Rhizaria, Foraminifera) from the Nazaré Canyon (Portuguese margin, NE Atlantic). Deep Sea Research Part II: Topical Studies in Oceanography, 58(23), 2401-2419. https://doi.org/https://doi.org/10.1016/j.dsr2.2011.04.005
Hsu, H. F., Krekhov, A., Tarantola, M., Beta, C., & Bodenschatz, E.. (2019). Interplay between myosin II and actin dynamics in chemotactic amoeba. New Journal of Physics, 21(11), 113055. https://doi.org/10.1088/1367-2630/ab5822
Gueron, S., Levit-Gurevich, K., Liron, N., & Blum, J. J. (1997). Cilia internal mechanism and metachronal coordination as the result of hydrodynamical coupling. Proceedings of the National Academy of Sciences of the United States of America, 94(12), 6001–6006. https://doi.org/10.1073/pnas.94.12.6001
Korohoda, W., Mycielska, M., Janda, E., & Madeja, Z. (2000). Immediate and long-term galvanotactic responses of Amoeba proteus to dc electric fields. Cell motility and the cytoskeleton, 45(1), 10–26. https://doi.org/10.1002/(SICI)1097-0169(200001)45:1<10::AID-CM2>3.0.CO;2-T
Lämmermann, T., & Sixt, M. (2009). Mechanical modes of ‘amoeboid' cell migration. Current Opinion in Cell Biology, 21(5), 636-644. https://doi.org/https://doi.org/10.1016/j.ceb.2009.05.003
Lauga, E. (2007). Continuous breakdown of Purcell's scallop theorem with inertia. Physics of Fluids, 19. https://doi.org/10.1063/1.2738609
Lauga, E. (2011). Life around the scallop theorem [10.1039/C0SM00953A]. Soft Matter, 7(7), 3060-3065. https://doi.org/10.1039/C0SM00953A
Lewis, Owen L., et al. “Coordination of contractility, adhesion and flow in migratingphysarumamoebae.” Journal of The Royal Society Interface, vol. 12, no. 106, 2015, p. 20141359, https://doi.org/10.1098/rsif.2014.1359.
Masaki, N., Miyoshi, H., & Tsuchiya, Y. (2007). Characteristics of motive force derived from trajectory analysis of Amoeba proteus. Protoplasma, 230(1), 69-74. https://doi.org/10.1007/s00709-006-0187-x
Matsumoto, K., Takagi, S., & Nakagaki, T. (2008). Locomotive Mechanism of Physarum Plasmodia Based on Spatiotemporal Analysis of Protoplasmic Streaming. Biophysical Journal, 94(7), 2492-2504. https://doi.org/https://doi.org/10.1529/biophysj.107.113050
Mogilner, A., & Oster, G. (1996). Cell motility driven by actin polymerization. Biophysical Journal, 71(6), 3030-3045. https://doi.org/https://doi.org/10.1016/S0006-3495(96)79496-1
Murrell, M., Oakes, P. W., Lenz, M., & Gardel, M. L.. (2015). Forcing cells into shape: the mechanics of actomyosin contractility. Nature Reviews Molecular Cell Biology, 16(8), 486–498. https://doi.org/10.1038/nrm4012
Mylnikov, A. P., Weber, F., Jürgens, K., & Wylezich, C. (2015). Massisteria marina has a sister: Massisteria voersi sp. nov., a rare species isolated from coastal waters of the Baltic Sea. European Journal of Protistology, 51(4), 299-310. https://doi.org/https://doi.org/10.1016/j.ejop.2015.05.002
NOOA, O. E. (August 26, 2010). Xenophores are singled cell animals called Protists. https://oceanexplorer.noaa.gov/explorations/05lostcity/logs/july27/media/xeno2.html
Purcell, E. M. (2012). Life at Low Reynolds Number. In Physics and Our World (pp. 47-67). WORLD SCIENTIFIC. https://doi.org/doi:10.1142/9789814434973_0004 10.1142/9789814434973_0004
Rapp, B. E. (2017). Chapter 9 – Fluids. In B. E. Rapp (Ed.), Microfluidics: Modelling, Mechanics and Mathematics (pp. 243-263). Elsevier. https://doi.org/https://doi.org/10.1016/B978-1-4557-3141-1.50009-5
Rivero, F. (2008). Endocytosis and the Actin Cytoskeleton in Dictyostelium discoideum. In International Review of Cell and Molecular Biology (Vol. 267, pp. 343-397). Academic Press. https://doi.org/https://doi.org/10.1016/S1937-6448(08)00633-3
Rode, S., Elgeti, J., & Gompper, G. (2021). Multi-ciliated microswimmers–metachronal coordination and helical swimming. The European Physical Journal E, 44(6), 76. https://doi.org/10.1140/epje/s10189-021-00078-x
Schaks, M., Giannone, G., & Rottner, K. (2019). Actin dynamics in cell migration. Essays in biochemistry, 63(5), 483–495. https://doi.org/10.1042/EBC20190015
Taylor, D. L., Condeelis, J. S., Moore, P. L., & Allen, R. D.. (1973). THE CONTRACTILE BASIS OF AMOEBOID MOVEMENT. The Journal of Cell Biology, 59(2), 378–394. https://doi.org/10.1083/jcb.59.2.378
Van Haastert P. J. (2011). Amoeboid cells use protrusions for walking, gliding and swimming. PloS one, 6(11), e27532. https://doi.org/10.1371/journal.pone.0027532
Wen, Q., & Janmey, P. A.. (2011). Polymer physics of the cytoskeleton. Current Opinion in Solid State and Materials Science, 15(5), 177–182. https://doi.org/10.1016/j.cossms.2011.05.002
Yoshida, K., & Soldati, T.. (2006). Dissection of amoeboid movement into two mechanically distinct modes. Journal of Cell Science, 119(18), 3833–3844. https://doi.org/10.1242/jcs.03152