Physical Principles Governing the Movement of Dinoflagellates and The Implications for Their Interactions in Aquatic Ecosystems
Thalia Azadian, Arda Barlas, Sophia Chen, Simon Girard
Abstract
Dinoflagellates are unicellular eukaryotic cells. There are around 2400 known species of dinoflagellates. This phylum is very diverse; among different species, we observe several unique characteristics of behavior and morphology. All dinoflagellates, however, have two flagella. These flagella allow them to swim in a unique and interesting manner. A dinoflagellate follows a helical motion produced by the motion of both its flagella. A change in the angular velocity ω2 of the transverse flagellum causes the cell to rotate on its longitudinal axis. In contrast, a change in the angular velocity ω1 and tangential velocity 𝜈 of the longitudinal flagellum is responsible for the orientation of the cell. By changing angular velocity ω, this microorganism can bend its swimming path to orient itself towards preferential chemical gradients. Helical movement is seen in most microorganisms living in low Reynolds number conditions which can be explained by the reduction of the Navier-Stokes equations into the Stokes equations. The combination of linearity and pseudosteadiness in the Stokes equation leads to reversibility, which explains why dinoflagellates have one of the most successful biological propulsion systems that bypass the constraints of the Scallop Theorem. Dinoflagellates also change their swimming direction to optimize nutrient uptake and avoid stressful waters, which has implications for dinoflagellate blooms.
Introduction
Aquatic ecosystems are teeming with life, from the smallest microorganisms to the largest marine creatures. Among the myriad of organisms that inhabit these environments, dinoflagellates stand out as both fascinating and ecologically significant. These remarkable organisms possess unique physical characteristics and exhibit intriguing behaviors that have implications for their functions in aquatic environments.
Dinoflagellates are a diverse group of single-celled, aquatic microorganisms that belong to the phylum Dinoflagellata. They are primarily found in marine environments, although some species can thrive in freshwater habitats. They are a unique group of protists that exhibit a wide range of shapes and characteristics, but they are typically characterized by their two flagella. The study of the motion of dinoflagellates begins with an exploration of their general morphology. These microscopic creatures, numbering in the hundreds of species, exhibit shared morphological characteristics while also boasting unique features that set each species apart. The field of fluid mechanics governing the locomotion of swimming microorganisms is an intricate field of study. Unlike larger organisms such as fish, these dinoflagellates navigate their aquatic environments within the framework of vastly different physical rules. Dinoflagellates have swimming mechanisms similar to that of fish, propelling themselves by generating waves of lateral displacement along a thin flagellum. However, the dynamics governing their movements are distinct. One important concept in understanding the motion of dinoflagellates is the Reynolds number, a dimensionless parameter recognized in fluid mechanics. This parameter quantifies the relative influence of inertial forces and viscous forces in a fluid's behavior when an object moves through it. Notably, while larger organisms like fish operate within Reynolds numbers on the order of thousands, swimming microorganisms, like dinoflagellates, operate at astonishingly low Reynolds numbers, often around 0.001 or even less. This disparity highlights the overwhelming significance of viscous forces in the dinoflagellates' motion, underscoring the complex interplay between their morphology and the surrounding fluid. Thus, by exploring the properties of flow at low Reynolds numbers and understanding their implications, we can further understand the locomotion strategies of dinoflagellates.
A Dinoflagellate's name represents its movement in water: dinos comes from the Greek word ‘whirling' and flagellum comes from the Latin word ‘a whip' (Carty & Parrow, 2015). Indeed, like most microorganisms with a low Reynolds number, dinoflagellates swim by helical movement through the motion of their two flagella: the transverse and the trailing flagella (Fenchel, 2001). Despite being faced with strong viscous forces, the helical path of the creature allows it to swim and orient itself in water (Fenchel, 2001).
Dinoflagellates also show changes in rheotaxic behavior changes in the face of unfavorable water conditions by performing cross-flow swimming or zig zagging. Furthermore, dinoflagellates prefer to swim against the current to expose themselves to an incredibly high volume of water. Furthermore, the rheotaxic behaviour of dinoflagellates has implications for dinoflagellate blooms, as it is shown that group swimming allows them to swim faster on average, and a congregation is more likely to form a dinoflagellate bloom under low turbulence ocean currents.
General morphology of dinoflagellates
To better understand the physical principles that affect mature dinoflagellates, we must first describe their general morphology. Of course, hundreds of species of dinoflagellates exist; each species shares morphological characteristics with other species, but also has its own unique characteristics. Therefore, the general morphology shared by most species of dinoflagellates will be described.
Dinoflagellates are eukaryotic single-celled organisms (Carty & Parrow, 2015). They have a large nucleus that can be up to 25-30% of the size of the entire cell (Carty & Parrow, 2015). It is often possible to see through the dinoflagellate to the nucleus (Carty & Parrow, 2015). Inside the nucleus, the chromosomes are permanently condensed (Carty & Parrow, 2015). In addition, dinoflagellates have mitochondria with cristae that are in tubular form (Carty & Parrow, 2015). Some photosynthetic dinoflagellates also notably have a red eyespot or stigma in the sulcal region (Carty & Parrow, 2015). Eyespots can have many functions. Among them, eyespot can function as light receptors, which is important for many photosynthetic dinoflagellates (Colley & Nilsson, 2016). Eyespots can also be used by some dinoflagellates for phototaxis (Colley & Nilsson, 2016). The red eye spot of a dinoflagellate is shown in Figure 1.

Figure 1: The eyespot of this dinoflagellate appears in red (Carty & Parrow, 2015).
Dinoflagellates also have unique organelles named trichocysts and pusules (Carty & Parrow, 2015). Trichocysts are spindle-shaped or rhomboid paracrystalline protein bodies (Levandowsky, 2012). When they undergo certain chemical or mechanical stresses, this structure expands to 8 times its former length, but it keeps the same diameter (Levandowsky, 2012). It is hypothesized that this mechanism has evolved to repel potential invaders (Levandowsky, 2012). Pusules are vesicular or tubular organelles located near the base of the transverse flagellum in the sulcus that has the following functions: macromolecule uptake, secretion, and osmoregulation (Carty & Parrow, 2015). Photosynthetic dinoflagellates contain chloroplasts usually found on the outskirts of the cell (Carty & Parrow, 2015). The chloroplasts have three membranes, thylakoids in stacks of three, and use chlorophyll A and C2 (Carty & Parrow, 2015). These cells usually appear golden in color due to the carotenoid peridinin (Carty & Parrow, 2015). Peridinin is one of the most abundant carotenoids in the world (Ishikawa et al., 2016). Phagotrophic dinoflagellates – dinoflagellates that obtain energy through the ingestion of food – have food vacuoles, accumulation bodies of material that can appear bright red, orange, or yellow, and may not have any chloroplasts (Carty & Parrow, 2015). Overall, they may appear pink (Carty & Parrow, 2015). Dinoflagellates use starch as an energy storage molecule and may sometimes also use oil (Carty & Parrow, 2015). Dinoflagellates come in very different sizes. Some only have a width and length of a few micrometers; other species can reach a few hundred micrometers long (Carty & Parrow, 2015). For example, Ceratium dinoflagellates measures around 400 in length (Carty & Parrow, 2015). Overall, dinoflagellates come in a wide variety of shapes and sizes, as illustrated in Figure 2.
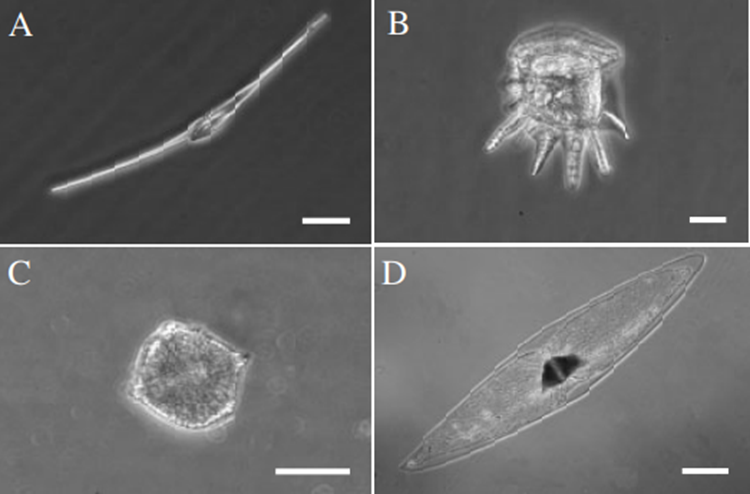
Figure 2: Example of the diversity of shapes found in dinoflagellates. In each of the four images is shown a different live cell of a bioluminescent dinoflagellate. In A, we have Ceratium fusus (the scale bar is 25μm); in B, we have Ceratocorys horrida (the scale bar is 25 mm), in C, we have Lingulodinium polyedrum (the scale bar is 25 mm); in D, we have Pyrocystis fusiformis (the scale bar is 100 mm) (Latz et al., 2004).
A typical dinoflagellate is divided into two portions: the anterior part is called the epitheca and the posterior part is called the hypotheca (in taxa without plates, these regions are called the epicone and hypocone, respectively) (Carty & Parrow, 2015). Dividing these two regions and usually encircling the middle of the dinoflagellate cell is a groove called the cingulum (Carty & Parrow, 2015). The cingulum may be found higher or lower on the cell, making the epitheca larger than the hypotheca, or vice versa (Carty & Parrow, 2015). Figure 3 depicts different parts and compartments found in dinoflagellates.

Figure 3: The different parts of a dinoflagellate (Carty & Parrow, 2015).
On the ventral side of the cell, a longitudinal groove named the sulcus extends along the hypotheca (Carty & Parrow, 2015). Two flagella that are used for swimming are found in a dinoflagellate cell (Carty & Parrow, 2015). First, a transverse flagellum is in the cingulum (Carty & Parrow, 2015). This flagellum allows the cell to move in a helical fashion when it swims (Carty & Parrow, 2015). Second, a longitudinal flagellum – sometimes referred to as the whiplash flagellum – is embedded in the sulcus (Carty & Parrow, 2015). It allows the cell to swim forward (Carty & Parrow, 2015). The longitudinal flagellum can extend out as much as 1.5 times the cell length (Carty & Parrow, 2015). Dinoflagellate cells are covered by a region called the amphiesma, which consists of multiple layers of material (Carty & Parrow, 2015). One of these layers is the plasma membrane (Carty & Parrow, 2015). Underneath the plasma membrane can be found the thecal plate armour (Carty & Parrow, 2015). This is a layer that acts as an armor, a sort of layer of protection for dinoflagellates (Carty & Parrow, 2015). It consists of vesicles that contain cellulose plates (Introduction to the Dinoflagellata). These plates vary in thickness between species (Introduction to the Dinoflagellata). Thecal plates often overlap (Introduction to the Dinoflagellata). If the cell expands, the plates may slide apart (Introduction to the Dinoflagellata). The plates can vary significantly in shape between species (see Figure 6) another marker for the impressive diversity found in dinoflagellates (Introduction to the Dinoflagellata). For example, Peridinium dinoflagellates have spherical plates, whereas Ceratium dinoflagellates have elongated horn-like plates (Introduction to the Dinoflagellata). However, not all dinoflagellates have thecal plates. Athecate cells do not have cellulose plates to protect them and so are more easily damaged. Some dinoflagellates have ridges and crests (Introduction to the Dinoflagellata). In nitrogen poor waters, the crests may even be hollow with nitrogen-fixing cyanobacteria symbiotically living inside (Introduction to the Dinoflagellata). The cyanobacteria provide the dinoflagellates with a source of fixed nitrogen (Introduction to the Dinoflagellata). Other dinoflagellate species, such as Ceratium fusus, may have apical (on the other side of the base) or antapical (on the same side as the base) horns or lobes (Figure 4). An example of a dinoflagellates crest and ridges can be seen in Figure 5.

Figure 4: Ceratium fusus, with its apical and antapical horn. Source: Ceratium fusus.

Figure 5: Example of crest and ridges in dinoflagellates (Introduction to the Dinoflagellata).

Figure 6: Line drawings of armored dinoflagellates. Where there is no line scale, refer to the text for cell size. (A) Exuviella compressa. (B) Gonyaulax spinifera. a, ventral; b, epitheca (s is a sulcal plate); c, hypotheca. (C) Thompsodinium intermedium. a, ventral (note trichocyst pores on plates); b, dorsal; c, epitheca; d, hypotheca. (D) Peridinium willei. a, ventral; b, dorsal; c, epitheca. (E) Peridiniopsis quadridens ventral. (F) Durinskia baltica. a, ventral; b, dorsal; c, epitheca. (G) Ceratium hirundinella, ventral H. Lophodinium polylophum. ventral. (I) Woloszynskia reticulata. a, dorsal; b, ventral; c, cyst. A, I are from Thompson (1950) with permission. C, E are from Carty (1989) with permission (Carty, 2003).
Flagella structure in dinoflagellates
Most dinoflagellates have a characteristic flagellar arrangement: a transversal flagellum that encircles the cell and, perpendicular to it, a trailing flagellum. Both flagella are inserted on what has been defined as the ventral side of the cell. The transversal flagellum is usually situated within an equatorial or slightly descending groove (the girdle or cingulum) and runs to the left, usually encircling the cell completely. The proximal part of the longitudinal flagellum lies freely in another groove referred to as the sulcus. The transverse flagellum is around twice as long as the longitudinal flagellum (Leadbeater & Dodge, 1967). Flagella are structures made of protein. Each flagellum is composed of 3 regions: the basal region that anchors the flagellum to the organism, the transition region where the flagellum exits the organism, and the external portion (Leadbeater & Dodge, 1967). The flagella itself, located on the outside of the cell, consists of part of a structure called an axoneme. An axoneme is made up of nine outer pairs of microtubules and two inner microtubules. The microtubules are made of tubulin protein dimers (Orbach & Howard, 2019). Between the inner and outer microtubules, there can be found secondary fibres (Leadbeater & Dodge, 1967). These secondary fibers are connected to the outer microtubules via fine fibrils (Leadbeater & Dodge, 1967). Packing material surrounds the axoneme; this material is itself surrounded by a flagellar sheath (Leadbeater & Dodge, 1967). The flagellum is thicker at the proximal part, thinner at the distal part, and ends in a round smooth tip (Leadbeater & Dodge, 1967). Fine hair around 0.5 long can be all over the flagellum, especially the distal part (Leadbeater & Dodge, 1967). The two inner microtubules stop at the basal plate, but the 9 outer pairs of microtubules continue down into the transition region (figure 7) (Vaughan & Gull, 2016). The transition zone serves as an attachment site for basal bodies (Dentler, 2009). Finally, dinoflagellates have two basal bodies – one for each flagellum – located inside the cell membrane. Upon reaching the basal bodies, the 9 outer double microtubules become 9 outer triple microtubules (Vaughan & Gull, 2016). Basal bodies are microtubule-based structures that assemble flagella (Vaughan & Gull, 2016). Basal bodies are connected to the cell's cytoskeleton through microtubule roots (Okamoto & Keeling, 2014). The longitudinal basal body is attached to the longitudinal microtubular root and single microtubular root; the transverse basal body is attached to the transverse microtubular root and transverse striated root (Okamoto & Keeling, 2014). Fibrous structures may connect the two basal bodies (Okamoto & Keeling, 2014)

Figure 7: microtubule distribution in axoneme, transition zone, and basal body (Vaughan & Gull, 2016).
Fluid mechanics of swimming microorganisms
Fish swims by causing a wave of lateral displacement to travel down its body from head to tail and this movement gives rise to circulations around the body which, in a fluid of low viscosity like water, are necessary to produce a forward force by dynamic reaction. In other words, the creature owes its ability to propel itself entirely to the inertial forces set up in the surrounding fluid by its muscular movements. Viscosity is important only insofar as it plays a part in the mechanics of the boundary layer, which in turn plays a part in determining the magnitude of the circulations with which the inertia reaction of the water is associated. The propelling organs of some very small living bodies bear a superficial resemblance to those of fish, in that propulsion is achieved by sending waves of lateral displacement down a thin tail or flagellum. The direction of movement of the organism is, like that of the fish, opposite to that of propagation of the waves of lateral displacement. However, the dynamics of a body as small as a dinoflagellate swimming in water is completely different from that of a fish (Taylor, 1951).
Most microorganisms live in a world dominated by viscous forces, governed by physical rules that are far different from those of macroorganisms and that are sometimes counterintuitive. To understand the movement of dinoflagellates we must first discuss the general fluid mechanics of viscous flows and their implications for swimming microorganisms (Guasto, 2012). Concepts such as the Reynolds number and the properties of flow at low Reynolds number can be investigated to explain this phenomenon and create an overall outline of the motion of dinoflagellates.
The Reynolds number
The Reynolds number (Re) is a dimensionless number used in fluid mechanics to describe the flow characteristics of a fluid around an object. The Reynolds number helps predict the flow regime of the fluid around the object and determines whether the flow is laminar or turbulent. It is used to assess the relative importance of inertial forces and viscous forces in a particular flow situation. When Re is small (Re<2000), the flow is considered laminar, meaning it is smooth and predictable. When Re is intermediate (Re~3000), the flow is in a transitional regime and can exhibit some characteristics of both laminar and turbulent flow. When Re is large (Re>4000), the flow is considered turbulent, characterized by chaotic, unpredictable motion, and mixing of the fluid (Jain, 2022).
The Reynolds number can also be described as the ratio of inertial forces to viscous forces. Mathematically, the Reynolds number for an object moving through a fluid is defined as:
Re=(interial force)/(viscous force)=pvL/μ
where L is some characteristic length defining the size of a body moving in water with velocity v, in a fluid of density p, and viscosity µ (Taylor, 1951). For most fishes, the Reynolds number is on the order of thousands, whereas very small organisms have very small Reynolds numbers on the order 0.001 or less. Therefore, the viscous forces, which might be considered insignificant when examining the movement of fish in relation to the much larger inertial forces, can be thousands of times more significant when dealing with swimming microorganisms. This is exactly the case when it comes to describing the motion of dinoflagellates.
Properties of flow at low Reynolds number
To discuss the properties of flow at Low Reynolds conditions, we must first define a fundamental concept in fluid mechanics called the Navier-Stokes Equations. The Navier-Stokes Equations is a set of partial differential equations that describe the behavior of fluid flow. The three-dimensional, incompressible form of the Navier-Stokes Equations is typically expressed using the Continuity Equation given by Equation 2 and the Momentum Equation given by Equation 3:
∇v=0 ~~~~~(2)
ρ(∂v/∂t+(v∙∇)v)=-∇p+μ∇^2 v+f ~~~~~ (3)
where v is the velocity vector field of the fluid, p is the scalar pressure field and f represents external forces applied to the fluid. The Continuity Equation represents the conservation of mass and ensures that the divergence (the rate of change of density) of the fluid velocity vector 𝑣 is zero, indicating that the fluid is incompressible. The Momentum Equation describes how the velocity field of a fluid evolves over time in response to various forces, including pressure gradients, viscous effects, and external forces.
The first two terms in Newton's second law on the left-hand side of Equation 3 represent inertial forces. The contribution of these terms is characterized by the Reynolds number and at very low Reynolds numbers of order 10-3– 10-5 the inertial forces are negligible (Khalil, 2021). Therefore, disregarding the inertial forces, Equation 2 and Equation 3 can be reduced to the Stokes Equations:
∇v=0 ~~~~~(2)
μ∇^2 v -∇p=-f ~~~~~ (3)
Unlike the Navier–Stokes equations, the Stokes equations are linear and time-reversible. The instantaneous structure of the flow does not depend on the history of the motion, but rather on the present configuration (Khalil, 2021).
The Stokes equations have several important properties that affect locomotion mechanisms in microorganisms. The first property is the equations' pseudosteady nature. The absence of a time derivative implies that temporal changes enter only by moving boundary conditions, such as flagella, to which the flow responds instantaneously. Consequently, the net motion of a swimming microorganism is independent of the rate at which its body deforms. Dinoflagellates are microorganisms that use flagella for propulsion. The pseudosteady behavior implies that the fluid flow responds instantaneously to the movement of their flagella. This is crucial for understanding how dinoflagellates generate propulsion by manipulating their flagella (Taylor, 1951).
Secondly, the Stokes equation is linear, and hence the solution of the flow fields around complex structures can be assembled by superposition. This linearity is important because dinoflagellates have intricate shapes and flagellar arrangements, and the linearity of the Stokes equation helps simplify the flow patterns around these organisms more easily.
The combination of linearity and pseudosteadiness in the Stokes equation leads to reversibility. Reversibility implies that a change in the boundary conditions, such as the reversal of flagellar movement, results in a change of sign in the velocity and pressure fields. For sustained swimming, a body must deform in a time-periodic fashion, but linearity and reversibility forbid reciprocal motions, those which appear the same when viewed forward and backward in time, from generating any propulsion. This is known as Purcell's Scallop Theorem, so named because it predicts that an organism or object with one degree of freedom (e.g., two rigid flaps connected by a hinge) cannot swim at low Reynolds numbers. In the context of dinoflagellates, this property is relevant because they have one of the successful biological propulsion systems that bypass the constraints of the Scallop Theorem due to their usage of a nonreciprocal flagellar motion for swimming (Taylor, 1951).
Now that we have a deeper understanding of the importance of the properties of flow at low Reynolds numbers for swimming microorganisms, we can investigate how dinoflagellates move under these conditions while also considering their general morphology and how their movement affects their overall behaviors.
Motion of dinoflagellates
Dinoflagellates have two flagella that contribute independently to their movement: a transverse flagellum and a longitudinal flagellum, also known as the trailing flagellum (Fenchel, 2001). These two flagella are perpendicular to each other with the transversal flagellum surrounding the creature's antero-posterior axis and the longitudinal flagellum attached on its posterior end (Miyasaka et al., 2004). A dinoflagellate is characterized by its helical movement which is the result of the motion of the movement of both flagella (Miyasaka et al., 2004).
Basic components of motion
The transverse flagellum allows for the forward thrust of the cell on the longitudinal axis (Miyasaka et al., 2004). Furthermore, the transversal flagellum rotates the cell on its longitudinal axis by modifying its angular velocity ω2 (fig 6(B)) (Fenchel, 2001). The transverse flagellum is said to have a helical beat pattern (Miyasaka et al., 2004). In contrast, the longitudinal flagellum, located on the posterior end of the cell, follows a sinusoidal wave pattern (Miyasaka et al., 2004). A dinoflagellate's flagellum creates waves from the base to the tip to move (Gaines & Taylor, 1985). Each beat is repeated without reversal (Gaines & Taylor, 1985). The longitudinal flagellum allows for the cell's orientation by the change of its angular velocity ω1 and/or tangential velocity 𝜈 as seen in Figure 8(B), following the equation 𝜈= ω1r (Fenchel, 2001). The trailing flagellum has the ability to independently control 𝜈 and ω1 by varying its direction and frequency (Fenchel, 2001).
To better illustrate the role of each unique flagellum, the following situations can be described. If a dinoflagellate has only a transversal flagellum, the creature would be “almost stationary” as it rotates (Fenchel, 2001, p. 330). In contrast, if a dinoflagellate has only a longitudinal flagellum, the dinoflagellate would move in circles (Fenchel, 2001).
The cell's helical movement is characterized by the sum of the angular velocities of the flagella: ω2 = ω12+ ω22, where the angular velocity ω is parallel to the helix axis as 𝜈 circles as shown in Figure 8(A) (Fenchel, 2001).
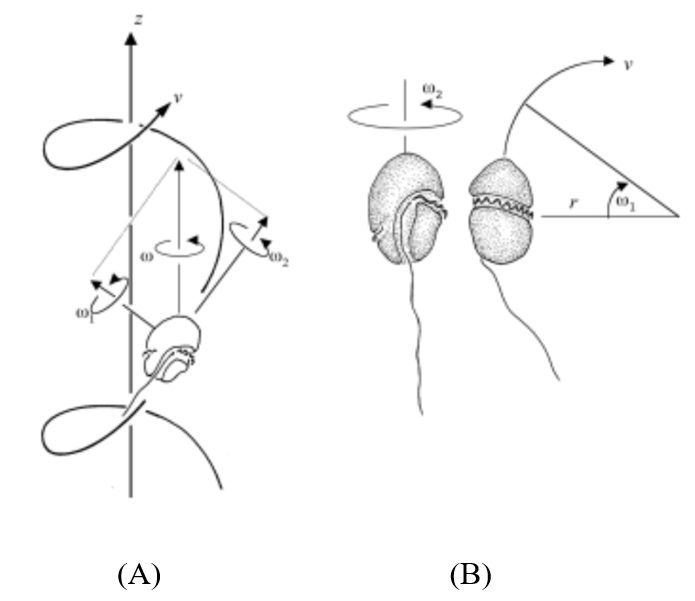
Figure 8: (A) Movement of a dinoflagellate along a helical axis with angular velocity components ω1, ω2, and ω. (B) Independent motion of each flagellum (Fenchel, 2001).
Swimming direction
Dinoflagellates can bend their swimming path by changing the pitch angle ϑ of the helical path (Fenchel, 2001). The pitch angle is the angle between the longitudinal axis – where the dinoflagellate is pointed – and the helix axis. The following equation illustrates the change in the pitch angle of the dinoflagellate: ω1/ ω2 = tan ϑ (Fenchel, 2001). Hence, by modifying the angular velocity of either the transverse or the trailing flagellum, the dinoflagellate can bend its path, allowing it to change directions as illustrated in Figure 9 (Fenchel, 2001). Commonly, dinoflagellates modify their angular velocity components for a length of 1-2 periods (T = 2π/ω) to move in a specific direction (Fenchel, 2001). This change can be executed by the adjustment of the beat frequency of the transversal flagella to alter ω2 (Fenchel, 2001). However, the dinoflagellate can also change its direction by altering ω1 by adjusting 𝜈 or simply by moving the direction of its trailing flagellum by contraction (Fenchel, 2001).
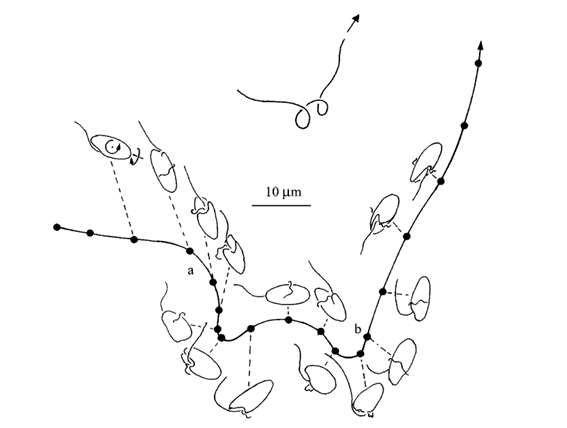
Figure 9: Point A illustrates an increase in the pitch angle of the helical path due to a change in the ω1/ ω2 ratio. Point B illustrates a decrease in the pitch angle to return to the conditions before the change in point A (Fenchel, 2001).
The rotation of a dinoflagellate takes place around its longitudinal axis with its ventral side facing the helix axis (Fenchel, 2001). Research has shown varying opinions on the direction of its rotation: left helix, right helix, or both (Fenchel, 2001).
The ability of the cell to change its swimming direction by varying one, two, or three parameters (ω1, ω2, 𝜈) is beneficial to a dinoflagellate as it can detect with more ease its preferred concentration chemical gradients (Fenchel, 2001). Indeed, these three variables are what allow this microorganism to move on a helical axis, hence exposing the creature to three dimensions of a gradient (Miyasaka et al., 2004). For example, if we have a space with XYZ coordinates, the helical movement of the dinoflagellate will allow it to sense with more ease changes in any one of these coordinates (Crenshaw, 1996). In contrast, if it did not have this locomotive property, it would only have access to one dimension, making it less efficient to spot preferred chemical gradients (Miyasaka et al., 2004).
A dinoflagellate's ability to orient itself towards a favored chemical gradient is called Helical Klinotaxis (Fenchel, 2001). Similar to how a moth flies towards light, dinoflagellates have a similar innate response to a chemical gradient. As a dinoflagellate travels perpendicularly to an increasing chemical concentration, it will change its helix axis by modifying its angular velocity ω to orient itself in the right component (Crenshaw, 1996; Fenchel, 2001). Once oriented in the right component, the dinoflagellate decreases its pitch angle by decreasing ω1/ ω2 to have its helix axis in alignment with the increasing gradient (Crenshaw, 1996; Fenchel, 2001). In contrast, if the microorganism detects decreasing chemical concentrations, it increases its pitch angle by increasing ω1/ ω2 to orient itself in the right direction (Crenshaw, 1996; Fenchel, 2001). Finally, once it reaches its preferred point, the dinoflagellate reduces ω2 to almost zero making it turn in circles in the area of interest, an effect seen in the example where a dinoflagellate only had a longitudinal flagellum (Fenchel, 2001).
Tendency to produce helical movement at low Reynolds number
Creatures orient themselves in their environment to find “food, mates, appropriate temperature, correct pH, sunlight, and many other factors important to life” (Crenshaw, 1996, p. 608). Hence, an organism's survival depends on its capacity to find these factors known as stimuli (Crenshaw, 1996). Microorganisms living under low Reynolds number conditions are often observed as having a helical path (Fenchel, 2001). Why is that? Researchers have hypothesized a few reasons why.
Firstly, in the same vein as the aforementioned benefits of a helical movement to detect a chemical gradient, a helical movement allows microorganisms to react to a stimulus more easily. Indeed, this movement allows the cell to better detect and orient itself in the direction of the stimulus (Crenshaw, 1996; Fenchel, 2001). Hence, this benefit has served as an explanation for the evolution of helical movement in microorganisms.
Secondly, as explained in the previous section, forces affecting an organism in low Reynolds number conditions are instantaneous. Furthermore, reciprocal motion does not allow an organism to advance in a fluid. For example, if a cell has paddle-like arms to propel itself forward, with each front and back stroke, the cell will move fluid up and down by the same amount, ending back in its initial position (Emberly, n.d.). Hence, microorganisms have developed asymmetric cyclic deformation to swim under such conditions (Purcell, 1977). With each deformation, a cell can translate and rotate, creating helical movement (Crenshaw, 1996).
Hence, a dinoflagellate's helical movement can be beneficial in both aspects: it allows it to travel and orient itself efficiently under low Reynold number conditions.
General significance and implications
Rheotaxis
Dinoflagellates, like many other protists use flagella to swim and gather nutrients by exposing itself through a large volume of water, often 106 times their own cell volumes (Nielsen & Kiørboe, 2021). For this to be achieved, dinoflagellates change their rheotactic behavior in response to different flow speeds. In stationary mediums, dinoflagellates mostly swim randomly (Li et al., 2021). When the flow speeds of water are between 20−40 μms-1, dinoflagellates tended to move against the flow, and are more likely to perform cross-flow swimming, slightly towards the current when fluid flows exceed 50 μms-1 (Li et al., 2021). By swimming against the current, the dinoflagellate is exposed to a large volume of water, and by extension the nutrients that are embedded within it. On the contrary, if the dinoflagellate swims toward fluid flow, it is stationary relative to the liquid, and nutrients cannot enter the dinoflagellate easily. Furthermore, the behavior of cross-flow swimming can be a mechanism to attempt to escape from more extreme liquid conditions in search of milder conditions to search for nutrients (Li et al., 2021).
In addition, viscous liquids slow down dinoflagellates' ability to collect inorganic nutrients (Nielsen & Kiørboe, 2021) and are generally correlated with a higher shear rate (Li et al., 2021). In general, the turbulence of a liquid can be measured with the Reynolds number, Re, and is defined in section 4.1. Furthermore, the shear rate γ. of a liquid is the speed at which two distinct layers of liquids move with respect to each other. It was observed that the flow speed and the shear rate are related through Reynolds number where a higher Reynolds number means that the shear rate is generally higher for a given flow speed (Li et al., 2021). In addition to viscous liquids slowing down dinoflagellates, high turbulence also introduces a higher mechanical stress towards dinoflagellates. It was found that this also led dinoflagellates to perform cross-flow swimming in an attempt to escape the current environment (Li et al., 2021). Moreover, even if dinoflagellates attempt to perform cross-flow swimming, they will adopt a zig-zag motion so that they still face the general direction of being against the current flow (Li et al., 2021).
Dinoflagellates moving to specific environments for better nutrients has significant ecological implications as dinoflagellates are known to cause blooms (Guzmán et al., 1990). Dinoflagellates, and in general phytoplankton, form a layer of biomass that extends for kilometers along coastlines and regions where they are sheltered from turbulent mixing (Durham, Kessler, & Stocker, 2009). It is found that gyrotactic trapping effects from hydrodynamic shear causes massive amounts of phytoplankton to be trapped just below maximum shear rates in the ocean (Durham, Kessler, & Stocker, 2009). This is confirmed by the fact that dinoflagellates congregate in regions that have hydrodynamic shear rates similar to the surface of the ocean (Li et al., 2021).
Conversely, it is found that turbulent flow is unfavorable towards dinoflagellate growth and reproduction (Karp-Boss, Boss, & Jumars, 2000), as strong shear rates would make it harder for dinoflagellates to maintain their vertical position, and swimming effects of dinoflagellates (Karp-Boss, Boss, & Jumars, 2000), which explains why it is much more difficult for dinoflagellate blooms to occur when there is strong turbulence in water (Karp-Boss, Boss, & Jumars, 2000). Even if there are strong disturbances, it is evident that dinoflagellates still prefer to swim against the current flow or attempt to do so, since they adapt a zig-zag motion when in oscillatory flow (Li et al., 2021).
When rheological conditions are moderate, the water conditions may still be too stressful for specific marine organisms. Therefore, a mechanism that is often adopted by participants in a bloom (not necessarily just dinoflagellates) to reduce the stress on weaker organisms is to have the strongest swimmers at the place where the density gradient is the greatest, and the weaker swimmers at the back where the density gradient is the lowest (Franks, 1992). Furthermore, while it may seem that the organism's bloom is stationary, a constant supply of new water and nutrients is supplied due to the ambient water flow (Franks, 1992). On the note of appearing stationary, because it is shown that dinoflagellates usually swim against the current flow to explore more waters (Li et al., 2021), it is plausible for the bloom to appear stationary, as being carried away by ocean currents does not allow dinoflagellates to obtain more food.
Being grouped together is also beneficial towards dinoflagellates' ability to obtain more nutrients. This benefits dinoflagellates. Firstly, because swimming in a long chain can reduce hydrodynamic drag forces for dinoflagellates, the group as a whole can swim faster compared to an average singular dinoflagellate (Karp-Boss, Boss, & Jumars, 2000). As previously established, swimming faster allows for dinoflagellates to explore more parts of the water and therefore have more food and nutrients (Karp-Boss, Boss, & Jumars, 2000). This also helps dinoflagellates in higher hydrodynamic shear rates if they need to swim perpendicularly to the flow. Karp-Boss et al. found that the average swimming speed for chains in the perpendicular direction increased due to shear, while the average swimming speed for individual cells decreased slightly for a shear rate of 1s−1, which generally correlates to very strong turbulence (Karp-Boss, Boss, & Jumars, 2000).
Flow disturbance
The movement of a dinoflagellate's flagella creates changes in the flow of water around the dinoflagellates (Nielsen & Kiørboe, 2021). Predators of dinoflagellates can pick up on these subtle changes in water pressure around the moving flagella (Nielsen & Kiørboe, 2021). This helps them locate where the dinoflagellates are. In addition, having two flagella – as many dinoflagellates do – is associated with a higher predation risk: more flagella cause more water disturbance that may be recognized by predators (Nielsen & Kiørboe, 2021). The less disturbance in the water a dinoflagellate creates, the less likely it is to be preyed upon. However, having two flagella and having powerful flagella can increase the dinoflagellates' ability to find food since it allows for quicker and more efficient movement (Nielsen & Kiørboe, 2021). Finding food is important for the success of a phagocytic dinoflagellate species. Having multiple flagella or powerful flagella comes with the downside of creating greater disturbances in water flow (Nielsen & Kiørboe, 2021). Therefore, there is a clear trade-off between resource acquisition and predation risk. Increased ability for resource acquisition comes with increased risk of predation, and vice versa.
Conclusion
An important consideration for a dinoflagellate's survival and reproductive success is how and where a dinoflagellate swims to ingest the most nutrients possible. Directly hunting for food is difficult and requires an advanced pathfinding method. As single-celled organisms, it is easier to swim through a large volume of water rather than attempt to find food manually. When a dinoflagellate is swimming against the current, the nutrients found in the water are moving towards it, leading the dinoflagellate to be exposed to more nutrients than if it was swimming in the same direction as current flow (Li et al., 2021). In the latter scenario, if the dinoflagellate had a velocity similar to that of the nutrients, it would be stuck with water that it has already processed. Dinoflagellates that are exposed to more nutrients have better survival and reproduction rates and therefore, natural selection favored dinoflagellates that swam against the current to acquire nutrients. Furthermore, marine protist blooms are a great solution for dinoflagellates to conserve energy while swimming upstream. By swimming upstream in a group, dinoflagellates and other marine protists can reduce hydrodynamic drag while also combing through large volumes of water (Karp-Boss, Boss, & Jumars, 2000). Energy conservation methods like this allow dinoflagellates to reduce their energy expenditure and increase their chances of survival.
Dinoflagellates with more optimal flagellar motion had a higher chance of survival and were more likely to reproduce. Millions of years of evolution culminated in the dinoflagellates following a helical swimming motion. This was the solution for how best to navigate in a low Reynolds number environment. Under such conditions, microorganisms are affected by linearity and pseudosteadiness, forcing them to swim with non-reciprocal movement. Hence, dinoflagellates have developed a helical swimming path to obey these constraints. Indeed, helical swimming is the result of asymmetric cyclic deformation, where each deformation causes a cell to translate and rotate in its environment (Crenshaw, 1996; Purcell, 1977). Moreover, dinoflagellates respond to stimuli in the form of chemical gradient – a process called Helical Klinotaxis (Fenchel, 2001), which is another reason for helical movement that dinoflagellates have developed to perceive changes in chemical gradients. This movement optimizes their ability to detect this stimulus as its helical path allows for detection in three dimensions. Upon the detection of a gradient, the dinoflagellates' two flagella reduce their angular velocity to approach the area of interest with more precision. Hence, with evolution, dinoflagellates have optimized their response to a stimulus in the form of a chemical gradient with the use of helical movement.
Studying the movement of dinoflagellates holds a critical importance to technological developments in the field of microrobots and nanorobots. With the significant improvement of integrated circuit manufacturing and the fabrication of smaller electric and mechanical components (Khalil, 2021), physical systems mimicking the locomotion of dinoflagellates and other swimming microorganisms can be developed and integrated into the biotechnology industry.
References
Carty, S., & Parrow, M. W. (2015). Chapter 17 – Dinoflagellates. In J. D. Wehr, R. G. Sheath, & J. P. Kociolek (Eds.), Freshwater Algae of North America (Second Edition) (pp. 773-807). Academic Press. https://doi.org/https://doi.org/10.1016/B978-0-12-385876-4.00017-7
Carty, S. (2003). 20 – DINOFLAGELLATES. In J. D. Wehr & R. G. Sheath (Eds.), Freshwater Algae of North America (pp. 685-714). Academic Press. https://doi.org/https://doi.org/10.1016/B978-012741550-5/50021-0
Ceratium fusus. Phyto'pedia – The Phytoplankton Encyclopaedia Project. Retrieved September 30 from https://phytoplankton.eoas.ubc.ca/research/phytoplankton/dinoflagellates/ceratium/c_fusus.html
Colley, N. J., & Nilsson, D. E. (2016). Photoreception in Phytoplankton. Integrative and Comparative Biology,
Dentler, W. (2009). Chapter 10 – Microtubule–Membrane Interactions in Chlamydomonas Flagella. In E. H. Harris, D. B. Stern, & G. B. Witman (Eds.), The Chlamydomonas Sourcebook (Second Edition) (pp. 283-307). Academic Press. https://doi.org/https://doi.org/10.1016/B978-0-12-370873-1.00047-2
Introduction to the Dinoflagellata. University of California Museum of Paleontology. Retrieved October 2 from https://ucmp.berkeley.edu/protista/dinoflagellata.html
Ishikawa, C., Jomori, T., Tanaka, J., Senba, M., & Mori, N. (2016). Peridinin, a carotenoid, inhibits proliferation and survival of HTLV-1-infected T-cell lines [Article]. International Journal of Oncology, 49(4), 1713-1721. https://doi.org/10.3892/ijo.2016.3648
Leadbeater, B., & Dodge, J. D. (1967). An electron microscope study of dinoflagellate flagella [Article]. Journal of general microbiology, 46(2), 305-314. https://doi.org/10.1099/00221287-46-2-305
Levandowsky, M. (2012). Chapter 49 – Physiological Adaptations of Protists. In N. Sperelakis (Ed.), Cell Physiology Source Book (Fourth Edition) (pp. 873-890). Academic Press. https://doi.org/https://doi.org/10.1016/B978-0-12-387738-3.00049-4
Nielsen, L. T., & Kiørboe, T. (2021). Foraging trade-offs, flagellar arrangements, and flow architecture of planktonic protists [Article]. Proceedings of the National Academy of Sciences of the United States of America, 118(3), Article e2009930118. https://doi.org/10.1073/pnas.2009930118
Okamoto, N., & Keeling, P. J. (2014). A comparative overview of the flagellar apparatus of dinoflagellate, perkinsids and colpodellids [Review]. Microorganisms, 2(1), 73-91. https://doi.org/10.3390/microorganisms2010073
Orbach, R., & Howard, J. (2019). The dynamic and structural properties of axonemal tubulins support the high length stability of cilia [Article]. Nature Communications, 10(1), Article 1838. https://doi.org/10.1038/s41467-019-09779-6
Vaughan, S., & Gull, K. (2016). Basal body structure and cell cycle-dependent biogenesis in Trypanosoma brucei [Review]. Cilia, 5(1), Article 5. https://doi.org/10.1186/s13630-016-0023-7
Crenshaw, H. C. (1996). A New Look at Locomotion in Microorganisms: Rotating and Translating. American Zoologist, 36(6), 608-618. http://www.jstor.org.proxy3.library.mcgill.ca/stable/3884000
Emberly, E. (n.d.). Topic 9: Fluids and Swimming Low Reynold's Number. Simon Fraser University. Retrieved 10/2/2023 from http://www.sfu.ca/~eemberly/phys347/lectures/9_Fluids_Low_Reynolds.pdf
Fenchel, T. (2001). How Dinoflagellates Swim. Protist, 152(4), 329-338. https://doi.org/https://doi.org/10.1078/1434-4610-00071
Gaines, G., & Taylor, F. J. R. (1985). Form and Function of the Dinoflagellate Transverse Flagellum1. The Journal of Protozoology, 32(2), 290-296. https://doi.org/https://doi.org/10.1111/j.1550-7408.1985.tb03053.x
Miyasaka, I., Nanba, K., Furuya, K., Nimura, Y., & Azuma, A. (2004). Functional roles of the transverse and longitudinal flagella in the swimming motility of Prorocentrum minimum (Dinophyceae). Journal of Experimental Biology, 207(17), 3055-3066. https://doi.org/10.1242/jeb.01141
Purcell, E. M. (1977). Life at low Reynolds number. American Journal of Physics, 45(1), 3-11. https://doi.org/10.1119/1.10903
Taylor, G. (1951). Analysis of the Swimming of Microscopic Organisms. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 209, 447-461. https://doi.org/10.1098/rspa.1951.0218
Guasto, J. S., Rusconi, R., & Stocker, R. (2012). Fluid Mechanics of Planktonic Microorganisms. Annual Review of Fluid Mechanics, 44, 373–400. https://doi.org/10.1146/annurev-fluid-120710-101156
Jain, S. R., Paradkar, B. S., & Chitre, S. M. (2022). A Primer on Fluid Mechanics with Applications. https://doi.org/10.1007/978-3-031-20487-6
Khalil, I., Klingner, A., & Misra, S. (2021). Mathematical Modeling of Swimming Soft Microrobots. DOI: 10.1016/B978-0-12-816945-2.00010-9A hydrodynamic analysis of flagellar propulsion, J. J. L. Higdon
Durham, W. M., Kessler, J. O., & Stocker, R. (2009). Disruption of Vertical Motility by Shear Triggers Formation of Thin Phytoplankton Layers. Science, 323(5917), 1067-1070. https://doi.org/doi:10.1126/science.1167334
Franks, P. J. (1992). Sink or swim: Accumulation of biomass at fronts. Marine ecology progress series. Oldendorf, 82(1), 1-12.
Guzmán, H. M., Cortés, J., Glynn, P. W., & Richmond, R. H. (1990). Coral mortality associated with dinoflagellate blooms in the eastern Pacific (Costa Rica and Panama). Marine Ecology Progress Series, 60(3), 299-303. http://www.jstor.org/stable/24842215
Karp-Boss, L., Boss, E., & Jumars, P. A. (2000). Motion of dinoflagellates in a simple shear flow. Limnology and Oceanography, 45(7), 1594-1602. https://doi.org/https://doi.org/10.4319/lo.2000.45.7.1594
Li, S.-W., Lin, P.-H., Ho, T.-Y., Hsieh, C.-h., & Sun, C.-l. (2021). Change in rheotactic behavior patterns of dinoflagellates in response to different microfluidic environments. Scientific Reports, 11(1), 11105. https://doi.org/10.1038/s41598-021-90622-8
Nielsen, L. T., & Kiørboe, T. (2021). Foraging trade-offs, flagellar arrangements, and flow architecture of planktonic protists. Proceedings of the National Academy of Sciences, 118(3), e2009930118. https://doi.org/doi:10.1073/pnas.2009930118 Latz, M. I., Nauen, J. C., & Rohr, J. (2004). Bioluminescence response of four species of dinoflagellates to fully developed pipe flow. Journal of Plankton Research, 26(12), 1529-1546. https://doi.org/10.1093/plankt/fbh141