Mathematical Space-Filling Models and Applications in Adipose Tissue

Josh Negenman, Milana Farah, Michelle Sayeh, Edward Tong

Abstract

The mechanisms describing how objects occupy space are some of the most fundamental topics of study and can be applied to countless chemical, physical, and biological phenomena. This is a topic that people have sought to understand for millennia, and it remains an integral part of our understanding of many of nature’s ingenious systems. Adipose tissue is composed of lipid droplets encased inside of adipocyte fat cells which make up the tissue, all of which are densely packed to maximize space and energy efficiency. This dense packing is intrinsically related to the concepts present in many space-filling models. This paper will discuss major topics in the field of space filling, including platonic solids and 3D tiling, optimization of sphere packing, irregular uniform sphere packing, ellipsoid packing, and multi-sized sphere packing, followed by a brief overview of how these concepts can be applied to understand the hierarchical structures composing adipose tissue.

Introduction

The world is inherently unpredictable and chaotic, yet a balance is found in the regularity of nature’s patterns. These patterns recur in different contexts, from microscopic to macroscopic. In other words, the same principles repeat themselves at different scales, showcasing nature’s ingenuity. Some phenomena can be modeled mathematically to understand their engineering design principles.

Adipose tissue and cells are a perfect example of how such patterns are present on different scales. Their hierarchical structure obeys certain principles that benefit the organism. A close examination of the adipose tissue uncovers the approximately spherical shape of its cells, the adipocytes (Figure 1).  These cells enclose vacuoles filled with lipid droplets which are typically also spherical no matter the type of adipocyte (Figure 2). The brown and beige adipocyte contains several lipid vacuoles scattered around the mitochondria, while the white adipocyte is composed of a single large lipid vacuole taking up to 90% of the cytoplasm (Bolsoni-Lopes & Alonso-Vale, 2015).

Fig. 1. A three-dimensional illustration of approximately spherical brown adipocytes forming a tissue (Josan, 2018).

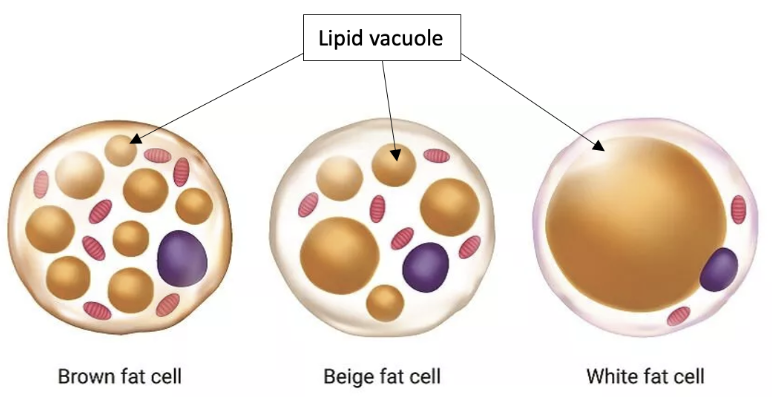
Fig. 2. Illustration of the lipid vacuoles contained in the different types of adipocytes (Adapted from Knapp, 2021).

Adipose tissue is found all over the body, under the skin, packed around internal organs and muscles, and within the bone marrow (Adipose Tissue | You and Your Hormones From the Society for Endocrinology, n.d.). In these spaces, the spherical cells arrange themselves in the most compact and efficient way. This paper will explore the mechanisms and modeling of space-filling and the different types of spherical and non-spherical packing, applying these fundamental principles to the various structural levels in adipose tissue.

Space filling and platonic solids

The study of patterns and shapes has been a topic of study for thousands of years. Early civilizations sought to understand fundamental geometric shapes and how they interact to fill space. Although the study of geometry and structures has been around for millennia, it remains a topic of research to this day, as it turns out to be a topic that is far from simple to understand.

Platonic solids, also known as regular polyhedra, are 3D structures with all identical faces. There are only five such structures that can exist in 3D Euclidean space: the tetrahedron (pyramid), the cube, the octahedron, the dodecahedron, and the icosahedron, with 4, 6, 8, 12, and 20 faces, respectively (Heilbron, 2013) (Figure 3).

Fig. 3. The five platonic solids that exist in 3D space (adapted from Heilbron, 2013).

Many natural phenomena can be studied by viewing them through the lens of space filling and 3D patterns, from the atomic scale all the way up to large physical phenomena. In the modern age of computers, much more extensive research can be done regarding the space filling characteristics of these solids, and patterns that are difficult to visualize can be found (Scott, 2011).

Tiling ℝ³

In order to maximize packing efficiency, and by extension maximize the use of space of a given assembly of structures, the goal is to minimize unused space between the structures being packed. In a perfect scenario, there is no space left between the structures in question. When it comes to platonic solids, this is more difficult than it may appear to be. There is one obvious case: the cube. Cubes can easily be assembled in such a way so as to leave zero space between them. However, no other platonic solid can fully tile the 3D Euclidean space ℝ³ due to the limitations in geometry. For one type of solid to be able to completely fill any space, the dihedral angles between solids must be either π or 2π. This is not the case for any platonic solid except the cube, which packs with dihedral angles of π (Gabbrielli et al., 2012).

Beyond cubic packing, the only other known ways to fully tile ℝ³ involve octahedra and tetrahedra. The most common method, known as the octet truss (Figure 4), was discovered by Buckminster Fuller and has a unit tile made up of one regular octahedron and two regular tetrahedra (with congruent vertex lengths). There are only two possible unit configurations with these base solids (Conway et al., 2011).

Fig. 4. Illustration of the octet truss, a tiling pattern capable of tilling ℝ³ with octahedra and tetrahedra with congruent vertex lengths (SeekPNG, n.d.).

It wasn’t until Conway et al. (2011) that a new configuration of platonic solids that can tile ℝ³ was discovered. By looking at the optimal packing of regular octahedra, it was found that the gaps left between the solids consisted entirely of smaller tetrahedra (Figure 5). By filling these gaps with smaller sized tetrahedra, the researchers found a family of 694 distinct tiling units composed of one octahedron and 5 smaller tetrahedra (Figure 6).

Fig. 5. A depiction of the holes associated with the optimal packing of octahedra. The octahedra are not shown, but the holes produced are filled with the red tetrahedra pictured (Scott, 2011).

Fig. 6. Depictions of different structures composed of larger octahedra and smaller tetrahedra capable of tiling ℝ³ (Scott, 2011).

Further research on the topic revealed the presence of four distinct ratios between the sides of tetrahedra and octahedra in a tessellation, all of which are related to certain packing schemes of either octahedra or tetrahedra, leaving holes that are tetrahedral or octahedral, respectively. These four so-called canonical tilings are the face-centered-cubic (FCC), the densest packing of octahedra (DO), the uniform packing of regular tetrahedra (UT), and parallel stacked layers of hexagonally packed octahedra (LO). Between these tilings, two families of infinite possible combinations of tessellations for ℝ³ can be derived (Gabbrielli et al., 2012).

As far as applications to uniform bodies such as cells, the most relevant topic is the optimal packing of more circular bodies, such as the optimal packing scheme of the dodecahedron or the icosahedron. In general, this results in a less efficient tiling of space, as ℝ³ cannot be tiled using these solids. This leads to the topic of sphere packing, as when you increase the number of faces of a polyhedron, it becomes closer and closer to a sphere.

Tilling is a fascinating way to study the possible combinations of solid objects of different sizes and how they can interact to fill 3D space. Though an abstract topic of study, the information gathered from studying the tiling of platonic solids can be applied to many real-world concepts, from the interactions and structures of crystals at the atomic level to applications in modern-day electronics (Scott, 2011).

Sphere packing

The sphere packing problem consists of arranging non-overlapping spheres in space in a way that maximizes the combined volume of the spheres (Sphere Packing | Brilliant Math & Science Wiki, n.d.) and consequently reduces the volume of the gaps between them. Although the problem may seem relatively simple, it took almost 400 years to solve (Nast, 2016). The classical case of the problem studies spheres of the same size in a 3D space. Still, it can be extended to consider different dimensions (higher or lower), different-sized spheres, and different shapes. Examples of this problem are ubiquitous, in the arrangement of particles in crystals, for instance, or even in the way oranges are stacked in the grocery store. 

In cases with very high dimensions (over 1000, for example), the densest packings are likely to be close to disorder. However, lattices – periodic arrays of points with good algebraic structure – make the densest packing in lower dimensions.

Circle packing in a 2D space

The simplest case, packing in a two-dimensional space, will be examined to understand the problem better. It consists of the arrangement of identical circles on a given surface such that no overlapping occurs. There are two possible ways to minimize the area separating them: square packing and hexagonal packing (Figure 7). It is apparent that the hexagonal packing, with 91% coverage, contains less empty space than the square packing, with 78% coverage (Lower, 2013). This realization is in accordance with the theorem proved by Fejes Tóth, stating that the hexagonal lattice is the densest of all possible plane packings (Circle packing – From Wolfarm Mathworld, n.d.).

Fig. 7. Square and hexagonal packing structures in a 2D space (Lower, 2013).

Sphere packing in a 3D Space

In three-dimensional space, different lattices originate from the superposition of different types of layers.

In the context of maximizing the efficiency (in terms of space occupied) of the structure, the three-dimensional close-packed structure is generated from numerous layers of 2D hexagonal packing. The positions of the different layers composing the 3D structure lead to different lattice types. In this kind of packing, the first layer of green spheres A is considered, as seen in Figure 8a. Two sets of equivalent void spaces exist between the layer A spheres: a blue set with a vertex pointed up and a white set with a vertex pointed down. The spheres of the second orange layer nestle in these voids created by the first layer. 

Subsequently, different placements of the third blue layer of spheres lead to two different types of close packing (Figure 8b). If the third layer is placed directly above the initial A-layer, the sequence obtained A-B-A-B-A… is characteristic of a hexagonal close-packed lattice (HCP). When the spheres of the third layer are placed over the unoccupied void spaces of the A-layer, an A-B-C-A-B-C-… sequence is achieved, representing a face-centered cubic lattice (FCC) (Lower, 2013).

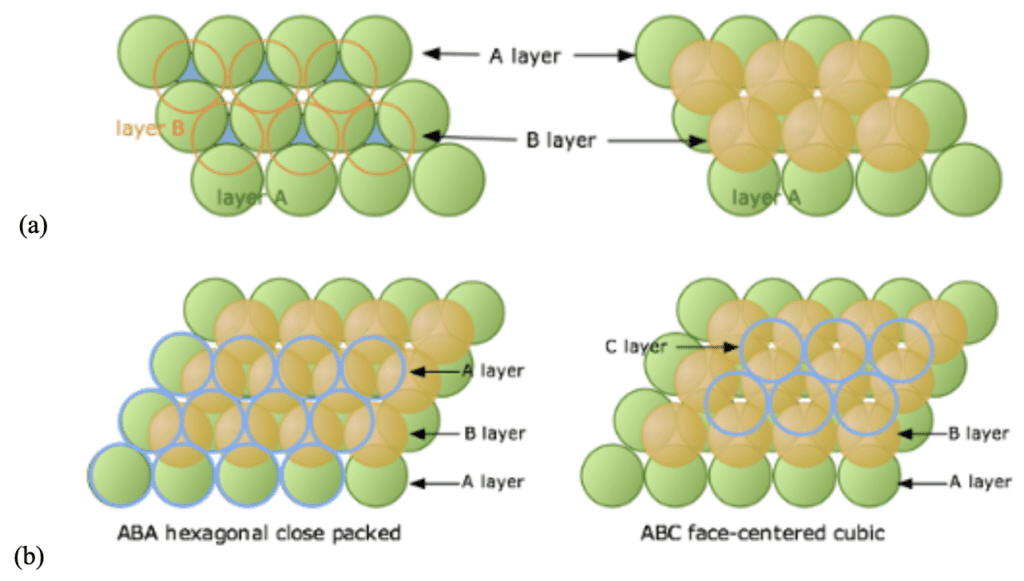
Fig. 8. (a) The placements of the second B-layer coloured in orange and (b) the different possible placement choices for the third C-layer over the B-layer (Lower, 2013).

Cubic packing

There are three types of cubic lattices, each corresponding to a type of cubic close packing: the previously mentioned face-centered cubic, the simple cubic lattice and the body-centered cubic lattice. A simple cubic lattice is created by superimposing layers of the square close packing discussed above in the 2D space. The different layers are made in such a way that the spheres of the upper layer are aligned with those of the previous layer. If the first layer were to be named A, then the lattice observed would follow a stacking sequence with an A-A-A-A… pattern (Close Packing in Solids- Three Dimensional Solids in Chemistry, n.d.). On the other hand, body-centered cubic (BCC) packing does not have closed-packed planes and therefore does not have a stacking sequence (FCC. BCC and HCP Metals, n.d.).

These structures can be visualized within unit cells, the smallest repeating portion in a lattice (Figure 9). A differentiating factor between the three cubic lattices is the number of spheres present in a unit cell. The simple cubic lattice, the FCC, the BCC, and the HCP possess 1, 4, 2 and 6 spheres per unit cell, respectively (Harbick et al., 2020).

Fig. 9. Simple cubic, face-centered cubic, and body-centered cubic unit cells (Unit Cells, n.d.).

Void spaces

No matter the sequence of spheres or the structure of the lattice, there are always void spaces that are not filled. Two classes of void spaces can be differentiated: tetrahedral (Figure 10a) and octahedral voids (Figure 10b). If the triangular void in a close-packed layer has a sphere directly over it, as seen in the case of the HCP structure, the void in question is surrounded by four spheres arranged on the corners of a regular tetrahedron. An octahedral void is formed at the center of six spheres when a triangular void pointing up in one layer is covered by a triangular hole pointing down in the adjacent layer. The latter exists in FCC structures (Krishna & Pandey, 1981).

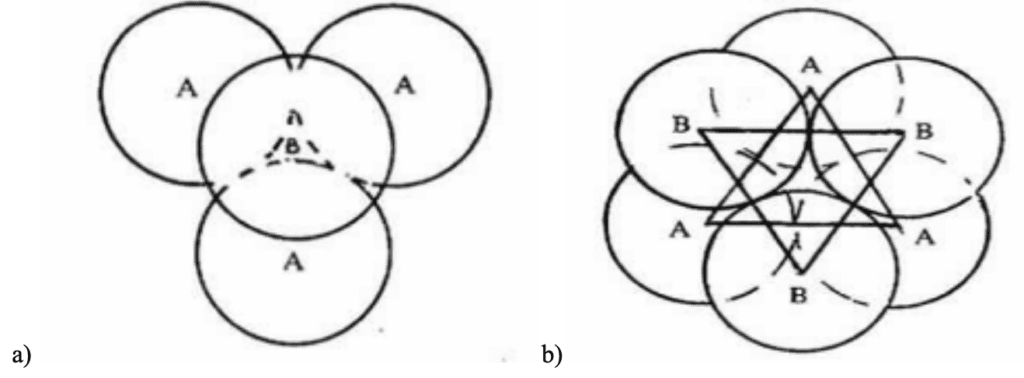
Fig. 10. a) A tetrahedral void resulting from a sequence found in HCP structures and b) An octahedral void resulting from a sequence found in an FCC structure (Krishna & Pandey, 1981).

Packing density

The packing density η of the above structures is measured to evaluate their efficiency. This refers to the fraction of the volume filled by the spheres constituting it. It is computed with the following expression (Conway & Sloane, 1999):

\eta=\frac{volume\;of\;one\;sphere}{volume\;of\;fundamental\;region}

Kepler’s conjecture, later accepted as a theorem proven by Thomas Hales, states that HCP and FCC packing structures are the densest possible, with identical packing densities (Sphere Packing — from Wolfram MathWorld, n.d ). The result of the Kepler problem is illustrated by:

\eta_{Kepler}=\eta_{FCC}=\eta_{HCP}\approx0.7405

The packing density of 74.048% obtained in FCC and HCP structures greatly surpasses that of simple cubic and body-centered lattices. Following the formula for η, their respective packing densities are 0.524 and 0.68 (Sphere Packing — from Wolfram MathWorld, n.d.).

Interestingly, the packing density of non-spherical packing can exceed that of FCC and HCP, a topic which will be discussed later in ellipsoid packing.

Irregular packing of uniform spheres

Although the simplest and most mathematically efficient way of packing spheres is regular sphere packing (as explained earlier), it is not the only way. Some disordered packing modeling exists, such as random close packing (RCP).

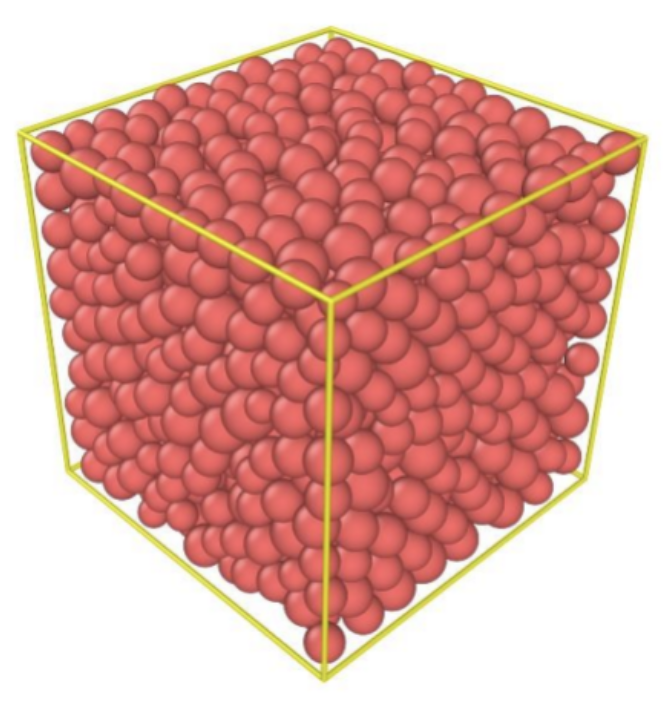
 Fig. 11. Modeling of random close packing of uniform spheres (Nie et al., 2017).

Random close packing occurs when a container is filled with an object, in this case, identical hard spheres, and then shaken until the spheres do not compact any further (Figure 11). In other words, it describes the maximum density a large random collection of spheres can attain (Torquato et al., 2000). This density is approximately 0.637 in three dimensions, much lower than the FCC density of 0.74.  However, despite the several experimental values of the RCP density, the calculation of these values remains mathematically ill-defined (Introduction to Granular Materials Jamming, Random Close Packing, n.d.). Therefore, many mathematicians proposed another mathematical concept called maximally random jammed state (MRJ), which has the same density as RCP but with a more accurate representation. The MRJ state refers to a single packing that is maximally disordered subject to the strict jamming constraint, regardless of its probability of occurrence in some packing protocol. Hence, the MRJ state is different from RCP (Torquato et al., 2000).

Uniform ellipsoid packing

One of the most interesting forms of packing non-spherical particles is the dense packing of ellipsoids with semi-axes a, b, and c, and aspect ratios α =b/a and β =c/a. An ellipsoid is a surface obtained by an affine deformation of a sphere which is an expansion of at least one of the sphere’s dimensions (Figure 12). Due to the change in shape, ellipsoid packing is slightly different from sphere packing.

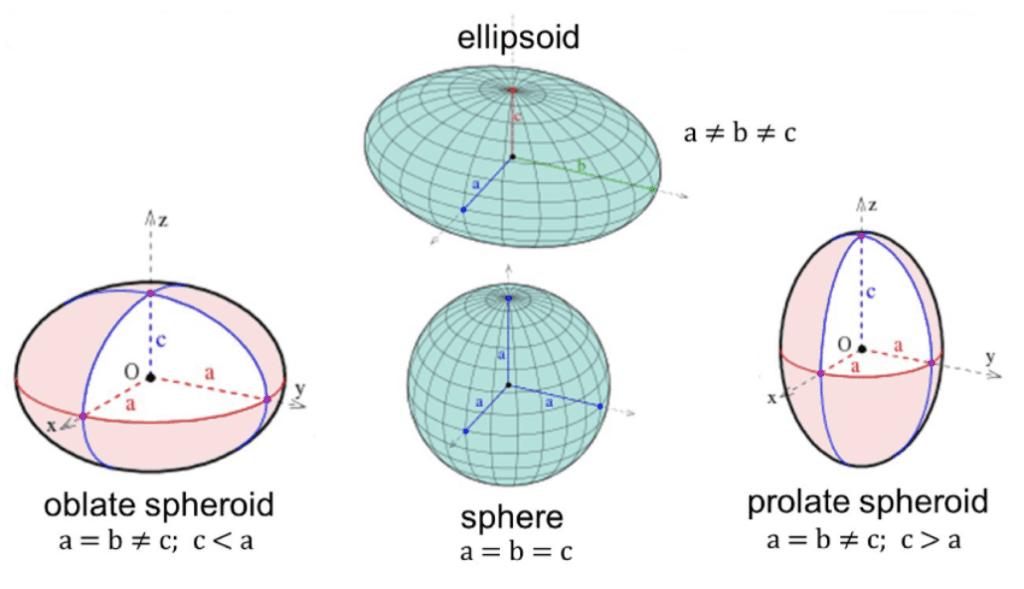
Fig. 12. The affine transformation of a sphere to obtain an ellipsoid (Singhal, 2018).

In two dimensions, the densest packing of these ellipses has the same density as the densest packing of circles, via hexagonal packing (η= 1√12 ≈  0.91). This maximal density is achieved by an affine transformation of the circles’ triangular lattice, which does not affect the density. In three dimensions, mathematicians always thought that ellipsoid packing had the same density as the densest packing of spheres, approximately equal to 0.7405. However, it has been found that this density is only accurate for lattice ellipsoid packing. In fact, non-lattice ellipsoid packing has proven to be even denser than FCC and lattice ellipsoid packing. By considering β = 1 , non-ellipsoid packing can reach up to 0.7707 with α = √3 for the prolate ellipsoid and α =1/√3 for the oblate ellipsoid, which is significantly denser than the FCC and HCP lattice of a sphere (η≈ 0.7405  ) (Figure 13). These are the two densest-known ellipsoid packing structures, with each ellipsoid having, in the face-centered layers, six rather than four in-plane neighbors and 14 touching neighbors overall (compared to 12 for the FCC lattice) (Donev et al., 2004).

Fig. 13. The density of ellipsoid packing as a function of the aspect ratio α  (considering β = 1 ). FCC: Face-centered cubic lattice sphere packing (close packing) (Adapted from Donev et al., 2004).

Multi-size sphere packing

Many problems in the chemical and physical sciences can be related to packing problems where variable sizes of spheres are available. When we consider mathematical aspects of the packing density in polydisperse sphere packing, particle size and distribution are the most significant assumptions in the modeling. The particle size distribution defines the contribution of each constituent of the mixture to the resultant density. There are two main methods for this packing: combining spheres of identical size in the same close-packed arrangement or packing the spheres following a decreasing size order. The second method is the most commonly observed (Burtseva et al., 2015). For example, if particles of two sizes are packed in the same container, the larger the ratio of the two sizes is, the higher the packing density.

When modeling a polydisperse packing, the spheres with the largest radius are placed first in a closed-packed arrangement. Then, the smaller spheres fill the gaps without expanding the structure (Figure 14). This is known as interstitial packing. However, when the smaller spheres’ radius is greater than 0.41 of the larger spheres’ radius, it is no longer possible to fill the gaps without rearranging the whole system, which will affect the overall density (Hudson, 1949).

Fig. 14. Modeling Multi-size packing involving two-sized spheres (Yamada S. et al., 2009).

Soap foam

One interesting example of space filling portraying another set of packing characteristics is in the structures of soap bubbles. The structure of clusters of soap bubbles obeys a set of simple rules defined by Plateau’s Laws (Figure 15). This set of rules can be split into two sets of observations. Firstly, in bubble arrangements in general, soap films are made of entirely smooth surfaces and the average curvature of a soap film is constant on any point on foam (Plateau’s Laws – Soft-Matter, n.d.). Furthermore, by using measure theory to study area minimization, Jean Taylor (1976) proved that three bubbles can only meet at angles of 120 degrees, forming an edge called a Plateau Border, and four bubbles meet at around 109 degrees.

Fig. 15. Various clusters of soap bubbles (Adapted from Getting to the Bottom of Foamy Physics – Physics World, 2013).

Applications in adipose tissue

The natural world will always arrange itself in such a way as to expend the least amount of energy to gain the most significant benefits. Therefore, adipocyte fat cells adopt a spherical shape, minimizing the surface area to volume ratio of the cells and thus improving the cells’ efficiency, even though ellipsoid packing has a higher density. However, it is impossible to pack spherical shapes in a continuous 3D array without leaving gaps. Adipocytes are densely packed and follow the optimal (hexagonal or BCC) spherical packing models discussed above, there is often an elegant solution to fill gaps in natural structures, such as in adipocytes, for which the void is filled with the connective tissue that links them together (Figure 16). This inherent characteristic illustrates the engineering ingenuity of nature.

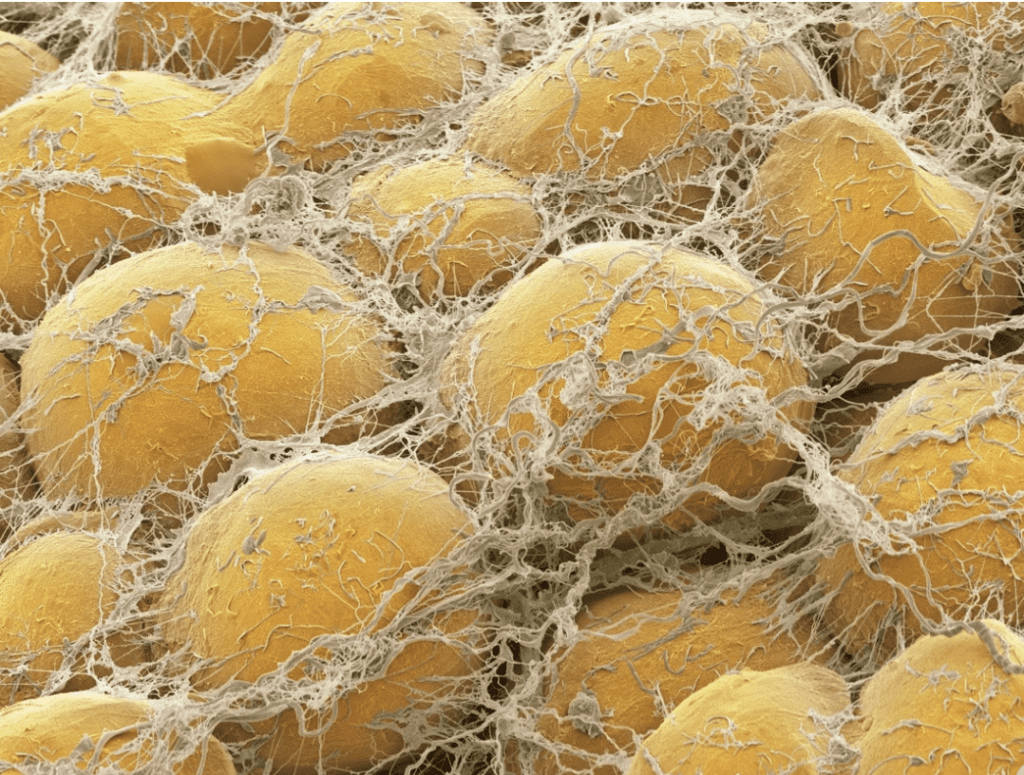
Fig. 16. Fat cells surrounded by strands of connective tissue filling in the voids between them and solidifying the structure (Pappas, 2018).

Lipid droplet shapes

Taking a step down the hierarchical ladder, inside the adipocyte, the next structure is studied: the lipid droplet. Fat droplets or lipid droplets are organelles residing in the cytoplasm of the cell (Figure 17). Unlike other organelles, only a single layer of phospholipids separates the neutral lipids, such as triglycerides, from the outside cytoplasm. However, just like many other organelles, these lipid droplets often take the shape of spheres with diameters ranging from 0.1 to 5 micrometers in non-adipocytes to over 100 micrometers in white adipocytes. One reason for their spherical shape is surface tension (Olzmann and Carvalho, 2020).

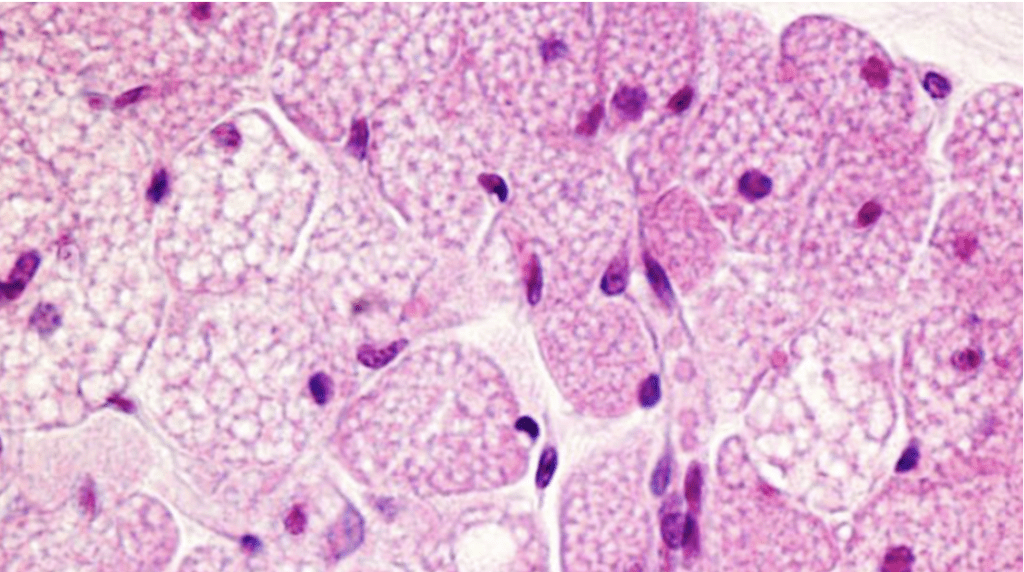
Fig. 17. Lipid droplets (white dots) in cells (purple dots = nuclei) (Calvo, 2016).

Surface-tension is a physical property of all liquids and is one of the main forces determining the shape of fat droplets. As the name suggests, it acts at or near the surface of the liquid and affects how it contacts not only other liquids but also gasses and solids. Surface tension is created at the molecular level by the force of one molecule pulling onto the other. This phenomenon is explained through the mathematical formula:

\begin{equation}
E=Me_0+S\cdot\sum t\rho(e-e_0)
\end{equation}

Where E is the potential energy of a liquid of mass M; e0 is the energy per unit mass of the interior liquid (internal energy); and e is the energy per unit mass for a layer of the surface S with thickness t and density ρ (surface energy). Under surface tension, the droplets reach the most stable shape i.e., the shape with the lowest potential energy: the sphere (Thompson, 2017).

That said, within the cell, the surface energy (e) may vary due to the non-homogeneous interior and chemical reactions occurring inside the cell. Thus, surface tension changes and molecules take on different forms. As well, surface tension forces of a droplet are also affected by the exterior factors such as the neighboring molecules it is in contact with, temperature, etc. For example, lipid droplets through only surface tension forces will move away from hotter areas while droplets of alcohols will move towards said warmer area. These environmental factors explain why, in media such as water, lipids take a more elliptical shape. Lipids are highly hydrophobic and thus try to form aggregates as compact as possible when in water. As previously mentioned, elliptical packing has a higher packing density, thus lipids take on these elliptical shapes; even if individually such shapes are less optimal, as a group it allows them to form denser droplets which reduce the overall potential energy (Thompson, 2017). 

Lipid droplet number and shape largely impact the overall shape of the adipocyte. White adipose cells primarily contain one large spherical lipid droplet and take the shape of a sphere while brown adipose cells are composed of dispersed lipid droplets and take a slightly more ellipsoidal shape. While not perfect spheres, both these structures follow the optimal spherical packing models described above, to optimize space and efficiency in the tissues (Richard et al., 2020).

Fig. 18. Packing of white adipocytes in a goat (scale bar = 50 micrometers) (Rajaii et al., 2021).

For millions of years, nature has developed and optimized systems and physical phenomena that scientists now try to understand and imitate. Adipose tissue is one such example, acting as insulation under the skin, cushioning around organs, and impact absorption/pressure distribution in digits (Wronska & Kmiec, 2012). These tissues are composed of densely packed adipocyte fat cells, of roughly equal size and spherical shape, which pack in a way so as to optimize space filled and the function of the tissue. Inside of these cells, there are lipid droplets that pack similarly to spherical or elliptical packing models due to surface tension, and to avoid high energy interactions. These layers of structures have been functionally optimized through evolution, from the densest packing models, to the most effective structures for a given function of the tissue, to the connective tissue filling the gaps. As humans try to unravel the mysteries of such natural structures, theoretical mathematical principles such as packing and space filling can be applied in order to understand the natural world.

Conclusion

 Nature is full of patterns, which are often arranged in a hierarchical order. In the case of adipose tissue, there are spherical or elliptical lipid droplets inside of spherical adipocyte fat cells, which pack together to form tissue structures that cushion, insulate, and fill space inside of organisms. This hierarchy of structures packing together can be studied under the single lens of packing and space filling, the most basic of which involves the packing mechanisms of uniform platonic solids. If we take platonic solids with many sides, namely the dodecahedron and icosahedron, and smooth them out, we are left with the sphere, which has packing models of its own. The sphere can then be squished to form ellipses, which follow different packing models and can be packed even more densely than spheres. Lipid droplets found inside brown adipose tissue (BAT) are sometimes elliptical and so will pack inside of the cells very densely similarly to these models. The large lipid droplets in white adipose tissue (WAT), as well as the adipocyte fat cells themselves, maintain spherical shapes, and pack in a hexagonal or BCC pattern, following nature’s recipe for optimal sphere packing. All told, these structures within structures have been optimized for space filling, and pack together perfectly to fill the spaces and roles required of them in an organism.

References

Bolsoni-Lopes, A., & Alonso-Vale, M. I. C. (2015). Lipolysis and lipases in white adipose tissue – An update. Archives of Endocrinology and Metabolism, 59(4), 335–342. https://doi.org/10.1590/2359-3997000000067 

Burtseva, L., Salas, B. V., Romero, R., & Werner, F. (2015). Multi-sized sphere packings: Models and recent approaches. Faculty of Mathematics, Otto-von-Guericke-Universität Magdeburg. https://doi.org/10.13140/2.1.4515.6169

Calvo, J. (2016, May 10). Brown adipocytes stained with Hematoxylin & Eosin. Alamy. Retrieved November 23, 2022, from https://www.alamy.com/brown-adipocytes-stained-with-hematoxylin-eosin-they-contain-many-small-lipid-droplets-distributed-throughout-the-cytoplasm-thus-acquiring-a-spong-image346976879.html?imageid=5E4D1F14-3D1B-4F68-A052-F34C230D043B&p=652981&pn=1&searchId=be59b2b40ba7bfc300c554e18b967785&searchtype=0

Circle packing – From Wolfarm Mathworld. (n.d.). Wolfram MathWorld. https://mathworld.wolfram.com/CirclePacking.html 

Close Packing in Solids- three dimensional solids in chemistry. (n.d.). BYJUS. https://byjus.com/chemistry/close-packing-three-dimensions/ 

Conway, J. H., Jiao, Y., Torquato, S. (2011). New family of tilings of three-dimensional Euclidean space by tetrahedra and octahedra. PNAS, 108(27), 11009-11012. https://doi.org/10.1073/pnas.1105594108 

Conway, J. H., & A. Sloane, N. J. (1999). Sphere Packings, Lattices and Groups (Vol. 290). Springer. https://doi.org/10.1007/978-1-4757-6568-7 

Donev, A., Stillinger, F. H., Chaikin, P. M., & Torquato, S. (2004, June 23). Unusually Dense Crystal Packings of Ellipsoids. Physical Review Letters, 92(25). https://doi.org/10.1103/physrevlett.92.255506

FCC. BCC and HCP Metals (n.d.) The University of Rhode Island. http://che.uri.edu/course/che333/Structure.pdf

Fujimoto, T., & Parton, R. G. (2011). Not just fat: The structure and function of the lipid droplet. Cold Spring Harbor Perspectives in Biology, 3(3). https://doi.org/10.1101/cshperspect.a004838

Gabbrielli, R., Jiao, Y., Torquato, S. (2012). Families of tessellations of space by elementary polyhedra via retesselations of face-centered-cubic and related tilings. Physical Review E, 86(4), 041141. https://doi.org/10.1103/PhysRevE.86.041141 

Getting to the bottom of foamy physics – Physics World. (2013, May 10). Physics World. https://physicsworld.com/a/getting-to-the-bottom-of-foamy-physics/

Harbick, B., Suh, L., & Fong, J. (2020). Closest Packed Structures. Chemistry LibreTexts. https://chem.libretexts.org/Bookshelves/Physical_and_Theoretical_Chemistry_Textbook_Maps/Supplemental_Modules_(Physical_and_Theoretical_Chemistry)/Physical_Properties_of_Matter/States_of_Matter/Properties_of_Solids/Crystal_Lattice/Closest_Pack_Structures 

Heilbron, J. L. (2013). Platonic solid. Encyclopedia Britannica. https://www.britannica.com/science/Platonic-solid 

Hudson, D. R. (1949). Density and Packing in an Aggregate of Mixed Spheres. Journal of Applied Physics, 20(2), 154–162. https://doi.org/10.1063/1.1698327

Introduction to Granular Materials Jamming, Random Close Packing, The Isostatic State. (n.d.). University of Rochester. http://www.pas.rochester.edu/~stte/BSSCM/lecture1.pdf

Josan, V. (2018). 3d Illustration of Fat cells abstract background Stock Photo. Alamy. https://www.alamy.com/3d-illustration-of-fat-cells-abstract-background-image214847009.html

Knapp, S. (2021, June 15). Adipocyte – The Definitive Guide | Biology Dictionary. Biology Dictionary. https://biologydictionary.net/adipocyte/

Krishna, & Pandey. (1981, January). Close-Packed Structures. University College Cardiff Press Cardiff, Wales. https://www.mrl.ucsb.edu/~seshadri/2005_218/iucr_close_packings.pdf

Lower, S., (2022). 7.8: Cubic Lattices and Close Packing. Chemistry LibreTexts. https://chem.libretexts.org/Bookshelves/General_Chemistry/Book%3A_Chem1_(Lower)/07%3A_Solids_and_Liquids/7.08%3A_Cubic_Lattices_and_Close_Packing 

Nast, C. (2016, April 2). Mathematician Solves the Centuries-Old Sphere Problem in Higher Dimensions. WIRED.  https://www.wired.com/2016/04/mathematician-solves-centuries-old-sphere-problem-higher-dimensions/ 

Nie, Z., Lin, Y., & Tong, Q. (2017). Modelling structures of open cell foams. Computational Materials Science, 131, 160–169. https://doi.org/10.1016/j.commatsci.2017.01.029

Pappas, S. (2018, April 4). What’s in a Fat Cell? livescience.com. https://www.livescience.com/62218-whats-in-a-fat-cell.html

Plateau’s laws – Soft-Matter. (n.d.). Harvard School of Engineering. http://soft-matter.seas.harvard.edu/index.php/Plateau%27s_laws

Rajaii, F., Kim, D. W., Pan, J., Mahoney, N. R., Eberhart, C. G., Qian, J., & Blackshaw, S. (2021). Temperature and species-dependent regulation of browning in retrobulbar fat. Scientific Reports, 11(1). https://doi.org/10.1038/s41598-021-82672-9

Richard, A. J., White, U., Elks, C. M., & Stephens, J. M. (2020, April 4). Adipose tissue: Physiology to metabolic dysfunction. National Library of Medecin. Retrieved November 24, 2022, from https://www.ncbi.nlm.nih.gov/books/NBK555602/

Scott, G. (2011, June 27). Princeton researchers solve problem filling space – without cubes. Princeton University. https://www.princeton.edu/news/2011/06/27/princeton-researchers-solve-problem-filling-space-without-cubes 

Singhal, R. (2018, May 21). Surface to Volume Ratio for a Spheroid, Cylinder, Cone and Rectangular Box – A Quantitative Analysis. Ektalks: Surface to Volume Ratio for a Spheroid, Cylinder, Cone and Rectangular Box – a Quantitative Analysis. https://ektalks.blogspot.com/2018/05/surface-to-volume-ratio-for-sphere.html

Sphere Packing | Brilliant Math & Science Wiki. (n.d.) Brilliant.org. https://brilliant.org/wiki/sphere-packing/ 

Sphere Packing — From Wolfarm MathWorld. (n.d.). Wolfram MathWorld. https://mathworld.wolfram.com/ 

Taylor, J. E. (1976). The Structure of Singularities in Soap-Bubble-Like and Soap-Film-Like Minimal Surfaces. The Annals of Mathematics, 103(3), 489. https://doi.org/10.2307/1970949

The Octet-truss Structure – Space Frame. (n.d.). SeekPNG. Retrieved December 10, 2022, from https://www.seekpng.com/ipng/u2w7o0r5w7w7w7w7_the-octet-truss-structure-space-frame/

Thompson, A. W. (2017, August 4). On growth and form by D’Arcy Wentworth Thompson. Project Gutenberg. Retrieved November 23, 2022, from https://gutenberg.org/ebooks/55264

Torquato, S., Truskett, T. M., & Debenedetti, P. G. (2000). Is Random Close Packing of Spheres Well Defined? Physical Review Letters, 84(10), 2064–2067. https://doi.org/10.1103/physrevlett.84.2064

Unit Cells. (n.d.). Course Hero. https://www.coursehero.com/study-guides/cheminter/unit-cells/ 

Wronska, A. & Kmiec, Z. (2012). Structural and biochemical characteristics of various white adipose tissue depots. Acta Physiologica, 205(2), 194-208. https://doi.org/10.1111/j.1748-1716.2012.02409.x Yamada S., Kanno J., & Miyauchi M. (2009). Multi-size Sphere Packing. Louisiana Tech University. https://www2.latech.edu/~jkanno/packing.pdf