Art in Symmetry: Mathematical Models that Dictate Radiolarian Structures

Vicky Barré, Liora Benzecry, Rhiannon Butler, Valerie Hung

Abstract

This essay explores the fascinating intersection of mathematics and biology through the study of Radiolaria, which are intricate marine protozoa known for their symmetrical skeletal structures. The idea of symmetry is the core of this investigation, highlighting how radial and bilateral formations in Radiolaria are not only aesthetically pleasing, but also crucial for evolutionary efficiency in energy usage and genetic coding. Furthermore, these structures can be mathematically modelled via Voronoi tessellations, Euler’s theorem, and geodesic sphere models. These models are essential for understanding the complex geometries and structural robustness of radiolarian skeletons. However, to perform these geometric analyses, sophisticated imaging methods such as sub-micrometer X-ray tomography are employed, which provide insight on the organisms’ complex structures and evolutionary adaptations at the nanoscale. In particular, the examination of geometric transformations in Radiolaria offers a window into the evolutionary history of these ancient organisms, shedding light on their morphological changes and adaptability over millions of years.

Introduction

The Earth’s vast animal kingdom is full of symmetry. From starfish to butterflies, apples to sunflowers, dandelions to Radiolaria, symmetry surrounds us. Symmetry in nature is not just seen in shape, but right down to the microscopic level. Nature’s bias towards symmetrical solutions comes from evolutionary theory. Although it is tempting to assume that symmetric designs arise from natural selection, evolution is not planned ahead. To survive, these traits must have some sort of immediate selective advantage. When an organism is developing, it is following a set of instructions set out in its genetic code. Instructions for symmetric structures are much easier to follow, and thus led to increased energy efficiency. Energetically efficient designs win out in the evolutionary arms race. In other words, symmetry does not arise only from natural selection, but also because the information related does not require increased complexity, thus reducing the risk of random mutations (Johnston et al., 2022).

Radiolaria have evolved to demonstrate various intricate skeletal shapes, from spherical to conical, that can be described using radial and bilateral symmetry. Even if classical geometric symmetry is important, order, regularity and proportionality in the structure of organisms are not always displayed as such. In fact, in situations where asymmetry is observed, it can be analyzed as a combination of symmetries (Afanasieva & Amon, 2014). This analysis can be done in the form of a variety of mathematical models. Applications of Voronoi tessellations as well as the geodesic sphere model shed light on the properties of spherically shaped Radiolaria. The application of mathematical concepts including Euler’s theorem, graph theory, and Euclidean geometry allows us to delve deeper into these beautiful skeletal shapes and the evolutionary timelines and pressures that led to them.

Symmetry

The word symmetry comes from the ancient Greek and means ‘agreement in dimensions, due to proportion, arrangement’ (Fortuna, S., & Savino, C., 2020). In mathematics, the word refers to objects that are invariant under a defined set of transformations, like reflection, translation, rotation, or scaling. In biology, symmetry is defined as a balanced, orderly distribution of body parts in living things. The symmetry of an organism’s exterior can be seen easily, such as the wings of a butterfly. Internal symmetry does not always reflect external symmetry. For example, many multicellular organisms have a singular heart that is on the body’s left side. The main transformations we consider to measure biological symmetry are rotation and reflection. Analyzing the symmetrical properties of Radiolaria allows us to study the implications of an organism exhibiting different types of symmetry.

Fig. 1. (a)Artistic renditions of radial symmetry in starfish and bilateral symmetry in flies. (Britannica, T. Editors of Encyclopaedia, 2021) (b)A beautiful example of symmetry in biology, the bilateral symmetry of butterfly wings. (Garvey, K. K., 2020) (c) Artistic rendition of asymmetry in sponges, radial symmetry in polyps, and bilateral symmetry in lobsters (Nielsen, N., 2016).

Radial symmetry

Radiolarians are intricate, architecturally beautiful organisms that get their name from the radial symmetry of their skeletons. In biology, radial symmetry is defined as rotational symmetry around an axis (Afanasieva, M., & Amon, E., 2014). The object’s degree of rotational symmetry is a characterization of its symmetric properties and is defined by the number of orientations in which the object looks identical after each rotation. The only objects that have full rotational symmetry at all angles are circular. Circular may refer to circles, spheres, or spheroids. The species of Radiolaria Cenosphaera cristata, Actinomma arcadophorum, Actinomma, Porodiscus, Alievium superbum, Crucella cachensis, and Sciadiocapsa radiata are all best modeled as spheres, and thus exhibit the highest degree of radial symmetry of all the Radiolaria (Afanasieva, M., & Amon, E., 2003).

Fig. 2. Photographs of spherically symmetric Radiolaria skeletons (a) Cyrtidosphaera reticulata Haeckel (b) Acanthosphaera circopora Popofsky (Yoshino et al., 2012).

When exploring radial symmetry, we can more formally define it using Euclidean geometry as a function of rotations in 3-dimensional Euclidean space. Euclidean spaces are geometry’s fundamental space that is defined as any positive integer dimension that is meant to represent the physical space (Menger, K., 1931). Since rotations are direct isometries, meaning they are transformations that do not flip the shape in question, the group of rotations that leave the object invariant is a subgroup of E ⁺(3). E ⁺(3) is the group of all transformations that preserve Euclidean distance between points. For spherically shaped Radiolaria, this group of rotations is larger since any axis passing through the center is an axis of symmetry. There are also certain Radiolaria that are more cylindrical in shape. Cylindrical symmetry is also a category of radial symmetry. However, cylinders only have one axis of continuous rotational symmetry, so cylindrical Radiolaria have a more limited group of rotations that leave the object unvaried.

Further radiolarian symmetry classifications

Regular polyaxonic symmetry is a specific type of radial symmetry seen in Radiolaria which is defined by having a higher order (Afanasieva, M., & Amon, E., 2014). The order is a numerical value that refers to the number of axes. This type of symmetry follows the rule that when the number of axes is reduced, it in turn reduces the number of lines that divide the body into identical fragments. The shapes of Radiolaria demonstrating regular polyaxonic symmetry include spherical and sphere derivatives.

Strauraxonic and monoaxonic symmetries are similar, as both involve only a singular axis of symmetry. The major difference between the two is their poles. A pole refers to the end of an axis, where it intersects the surface of the Radiolaria. The poles of the axes in stauraxonic symmetry are identical and thus are demonstrated by skeletons which have morphologically identical ends of their axes. This symmetry is what distinguishes the class Stauraxonaria from all other Radiolaria. In monoaxonic symmetry, the poles of the single axis are not identical and thus the line that separates the two identical halves is not always well defined. As such, monoaxonic Radiolaria are often elongated conical shapes which can be seen in the Pylomariata, Mesozoic–Cenozoic Nassellaria, and Phaeodaria orders.

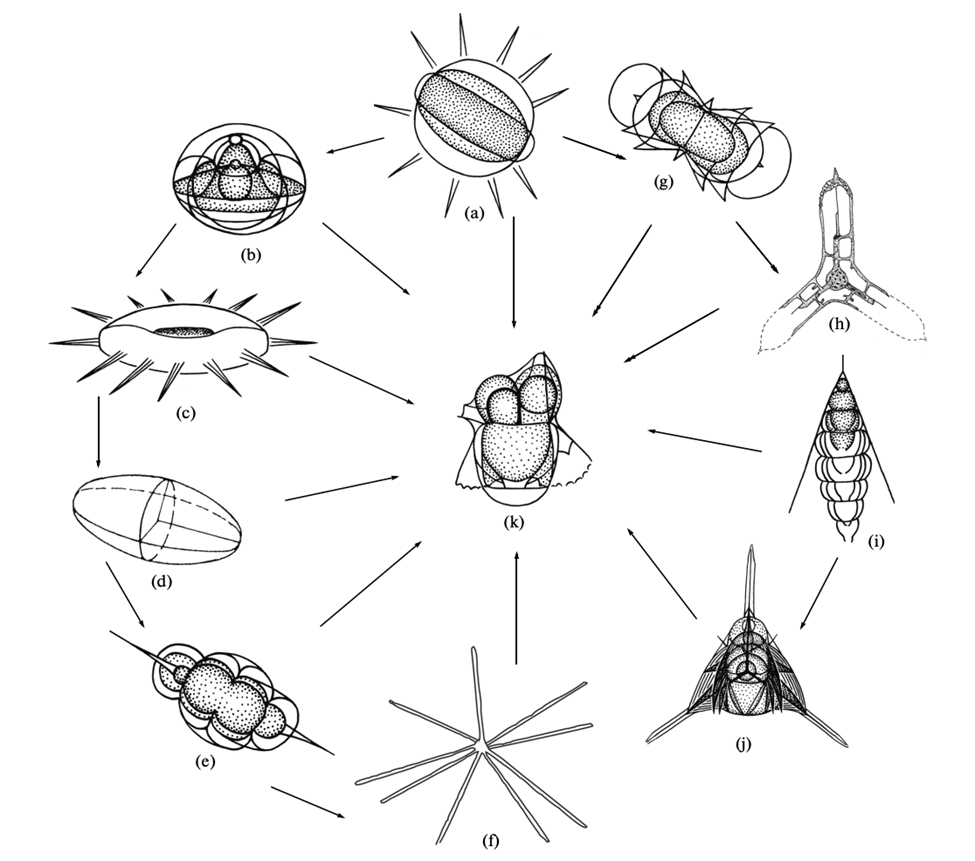
Fig. 4. Possible symmetries and sub symmetry classifications demonstrated by radiolarian skeletons. (a)Spherically symmetry. (b) Regular polyaxonic, a subset of spherical. (c-f) stauraxonic. (c) discoidal. (d) ellipsoidal. (e) spindle-shaped. (f) n-rayed. (g,h) radial. (g) dumbbell-shaped. (i, j) monoaxonic. (i) subconical. (j) tripod. (k) bilateral, varying shape (Afanasieva, M., & Amon, E., 2014).

Bilateral symmetry

Bilateral symmetry can be observed when we can divide the Radiolaria’s skeleton down one central axis and end up with two mirror-image halves. This type of symmetry is less common than radial in Radiolaria, however it can be seen in Figure 3. The difference between radial and bilateral symmetry is that bilateral symmetry only involves a single plane of symmetry, called the sagittal plane.

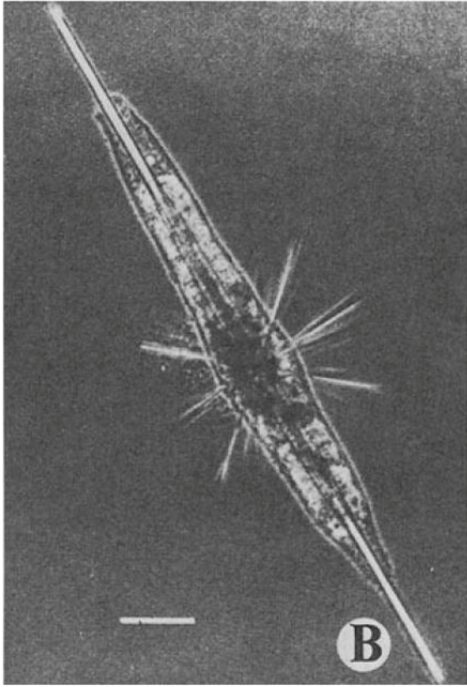
Fig. 3. A bilaterally symmetric species of Radiolaria, called Amphilonche elongata (Anderson, O. R., 2012).

Evolutionary importance

Different symmetries provide different solutions to problems faced in the daily life of Radiolaria. With such symmetry, they can respond to their environment and capture prey from all directions, without the need of a central nervous system.

The horizontal propagation of Radiolaria using their pseudopodia is not very fast or efficient, as such this marine protist relies heavily on riding ocean currents to get around. Having these bilaterally symmetric shaped skeletons allows them to optimize their transportation to overcome ineffective locomotion. When an organism is developing, it follows a set of instructions from its genetic code. Higher symmetry means these instructions are much more concise and thus require less energy to read and carry out. Energy conservation is the driving force behind much of nature’s design solutions, including this one (Afanasieva, M., & Amon, E., 2014).

Mathematical models

Classical geometry cannot always be directly applied to biology since nature is very complex. However, even asymmetry can be described using a combination of symmetries and explored using various models. By applying principles from graph theory, geometry, and computational imaging, scientists have been able to explore the fascinating world of Radiolaria beyond what is visible to the naked eye. For instance, in a study conducted by Jungck et al. (2019), they examined different radiolarian tests using X-ray CT scans, focussing on the polygonal distributions, and found spherical patterns of convex polygons (Fig. 5). Then, to analyze the geometric patterns on the radiolarian tests, the images were processed using Ka-me software. This analysis involved generating histograms to show the frequency of differently sided polygons and coloring the polygons within the convex hull of the radiolarian test for better visualization. A significant observation across the different tests was the predominance of hexagonal faces, with a modal number of six. This suggests a widespread presence of hexagons in the tessellation. However, to incorporate curvature and achieve sphericity in the structure, a combination of hexagons and pentagons is necessary. Indeed, pentagons were observed as the second most common shape (Fig. 6,7). This mixture of hexagons and pentagons, creating trigonal junctions (three vertices), is indicative of Voronoi tessellations adapted for spherical surfaces (Jungck et al., 2019).

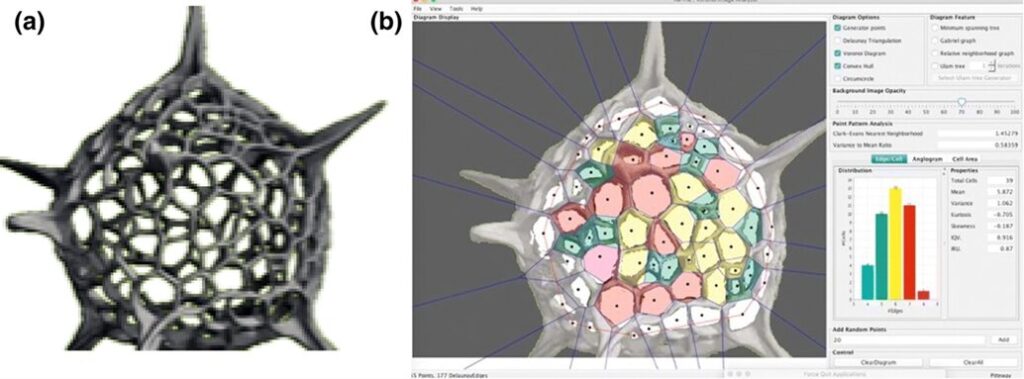
Fig. 5. (a) Detailed micro-focus X-ray CT scan of a radiolarian. (b) Ka-me analysis highlights the predominance of hexagonal shapes in the radiolarian’s structure. Structure takes on spherical patterns of convex polygons (highlighted in the different colours) (Jungck et al., 2019).

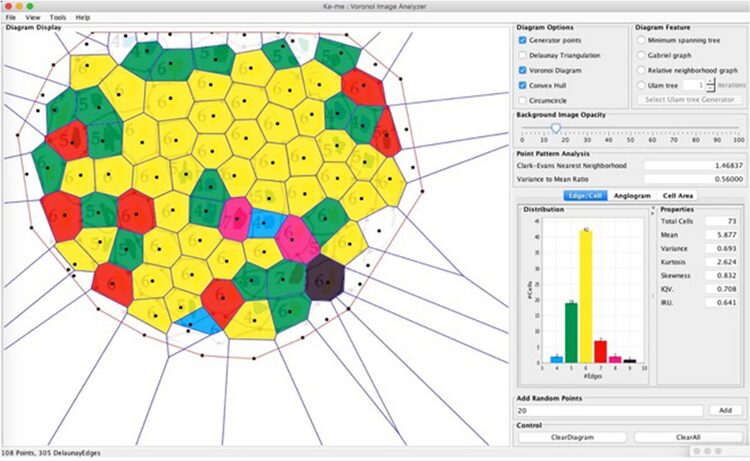
Fig. 6. Mathematical analysis of the radiolarian Acrospheara test. The test consists mostly of hexagons, but there is also a presence of 4-, 5-, 7-, 8-, and 9-sided convex polygons (Jungck et al., 2019).

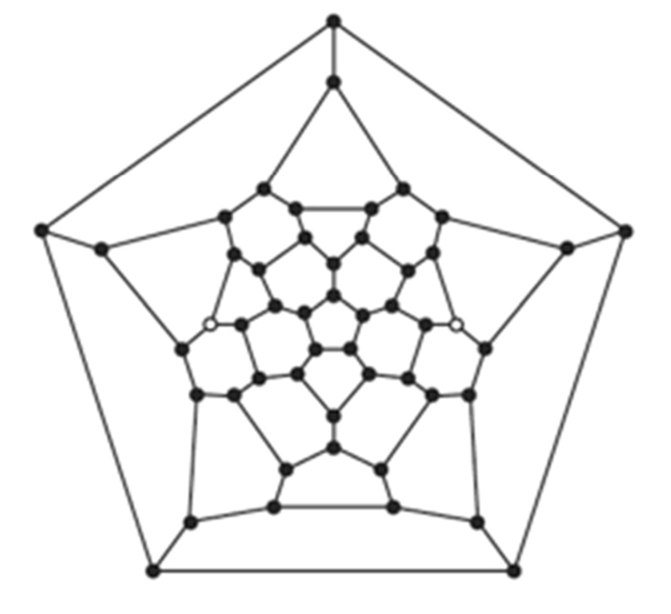
Fig. 7. A micro-focus X-ray CT scan of a Pantanellium radiolarian. This Schlegel diagram of the radiolarian test shows the topology of the 27 faces, which includes12 pentagons and 15 hexagons (Jungck et al., 2019).

Voronoi tessellations

Voronoi tessellations are a way of dividing a space into several regions based on distances to a specified set of points, known as Voronoi sites (Voronoi, 1908). Each point in a given region is closer to its corresponding Voronoi site than to any other site. For instance, imagine a plane in which several points (Voronoi sites) are scattered. The Voronoi tessellation separates the plane into regions around each point. For any given point in a region, it is closer to the Voronoi site of that region than to any other site. Each region formed in this way is called a Voronoi cell. The boundaries of these cells are equidistant from the neighboring sites and often form polygonal shape (Bellelli, 2023). An example of a Voronoi diagram can be seen below (Fig. 8):

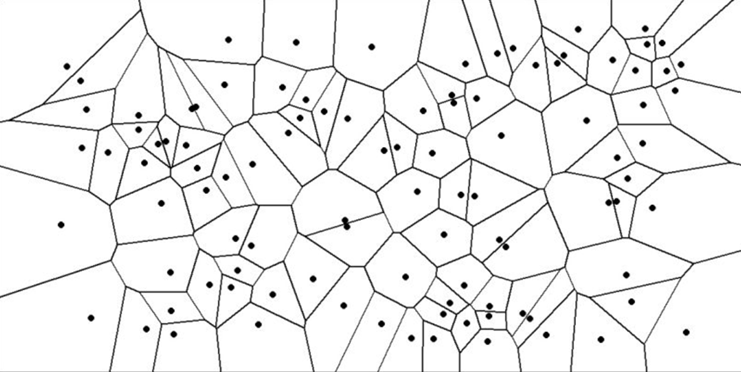
Fig. 8. Example of a Voronoi diagram (Bellelli, 2023).

In the context of Radiolaria, Jungck et al. (2019) suggests that the generation of spherical radiolarian tests is likely a result of short-range local interactions, since Voronoi tessellations are typically formed through nearest neighbor interactions (Fig. 9). Had it been long-range interactions, the result of the distribution of polygonal faces would be different.

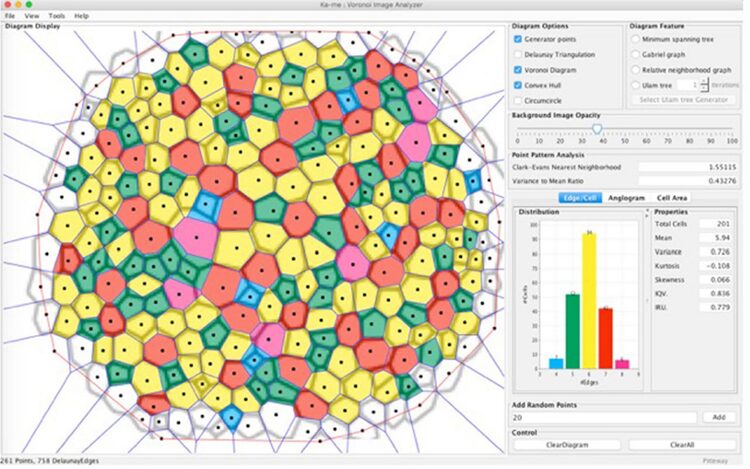
Fig. 9. Ka-me analysis on Haeckel’s Cyrtidosphaera reticulata. Using two spatial statistical tests: the Clark-Evans Neighborhood test and the Variance to Mean Ratio test. These tests suggest that the distribution of these polygons aligns more with a random than a uniform distribution, challenging the traditional understanding of Voronoi tessellation’s role in fitting these shapes. Although the Voronoi tessellation doesn’t perfectly fit, particularly for 8-sided polygons, it offers a heuristic approximation for understanding the distribution of convex polygons on the surface of the radiolarian test (Jungck et al., 2019).

Euler’s theorem

Furthermore, the findings from Jungck et al.’s (2019) study aligns with Euler’s theorem in graph theory, which states that for any convex polyhedron, the number of vertices, faces, and edges (E) must satisfy the equation the following equation:

|V| – |E| + |F| = 2

(V) number of vertices, (E) number of edges, and (F) number faces (Pickard, 2022).

A specific application of Euler’s theorem is commonly referred to as the “Soccerball theorem.” It explains that a sphere covered solely with hexagons and pentagons requires at least twelve pentagons to complete the tessellation, reflecting the constraints imposed by the Euler characteristic. In the context of Radiolaria, a particular species, Acrospheara, has 221 vertices, 149 faces, and 368 edges on their convex polyhedral tests, which perfectly aligns with Euler’s formula (221 – 149 + 368 = 2). This mathematical conformity underlines the inherent geometric nature of radiolarian structures.

The geodesic sphere models

The geodesic sphere model was investigated to describe internal structure of Phaeodaria, a deep-sea protozoa that is mostly referred to as radiolarians and classified into the polycystine group of Radiolaria. Such internal spherical structures are usually composed of an intricate geometric network made from opaline silica (SiO₂ • nH₂O). Such networks are characterized by the double layer of near-equilateral triangles, all arranged in a hexagonal lattice (Fig. 10). The double layer is formed by connected vertical rods at each intersection of the triangles. In other words, two networks of the hexagonal lattice form the double layer due to those rods at each vertex that brings them together.

Fig. 10. The repeated silica lattice of a hexagonal prism sectioned into equilateral triangles imaged using scanning electron microscopy (SEM) (Beittenmiller, 2015).

Equilateral triangles can distribute stress evenly on all sides, thus, having multiple in a geodesic sphere or dome also allows the distribution of external stress evenly. On the technical side, such structures can withstand a good amount of pressure without the need for support rods on beams on the inside. Additionally, due to the identical faces, their assembly is simple, which suggests efficiency on a biological level, requiring less energy from the organisms as mentioned earlier (Beittenmiller, 2015).

Polyhedrons are the base level of geodesic spheres, being characterized by their frequency k. Such frequency describes the number of subdivisions that each face or triangle has in the structure (Fig.11). For example, when k = 1, there is only one undivided triangle that covers the sphere. When k = 2, for the same sized triangle, there are now 3 triangles inside that original triangle, so in total 4 triangles can be counted. That original triangle is divided into more and more triangles as the frequency increases, but the sides and size are preserved (Beittenmiller, 2015). Amongst the different types of polyhedrons as bases, icosahedron and dodecahedron demonstrate uniform triangle sizes and lengths all over the surface. Icosahedrons have 12 faces and 20 vertices while dodecahedrons have 20 faces and 12 vertices (Fig.12). At higher frequencies, icosahedron-based spheres and dodecahedron-based spheres are almost identical (Fig.13). In such polyhedrons, their faces are represented as pentagonal (dodecahedron) or hexagonal (icosahedron), of which each face also represents grouped triangles as illustrated in Figure 13, but it is difficult to concentrate and determine if any distortion is visible. For this geometric pattern, Euler’s theorem, demonstrated above, is applicable. However, a derivative from Euler’s law is also important (Beittenmiller, 2015):

Σ (6-n)F_n = 12

Such formula is applied for convex polyhedra with nodes where 3 corners meet. The number of sides on a single face is represented by n, F_n being the number of faces having n sides and (6-n) shows that, in such geodesic spheres, the model is not fully composed of hexagonal faces, but rather a mixture of both, where 12 pentagonal faces are present. Which can account for the irregularities or exceptions in the lattice of polycystine radiolarians (Beittenmiller, 2015).

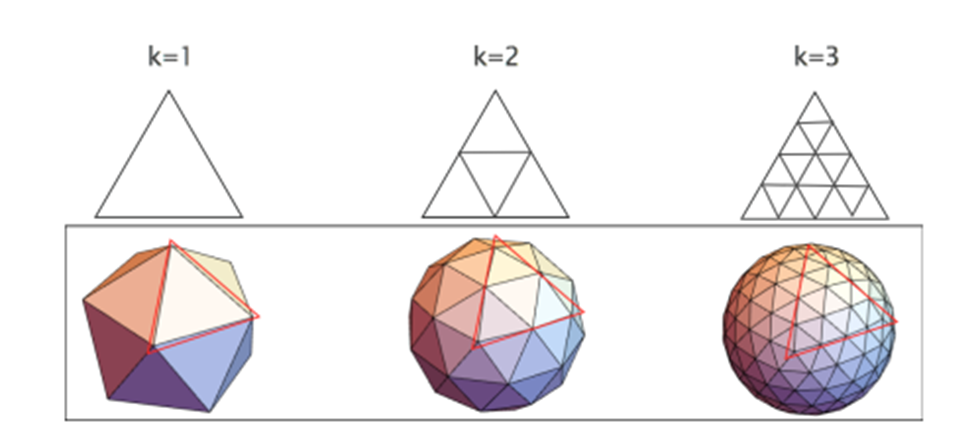
Fig.11. Icosahedron geodesic spheres with frequencies 1 to 3 (Beittenmiller, 2015).

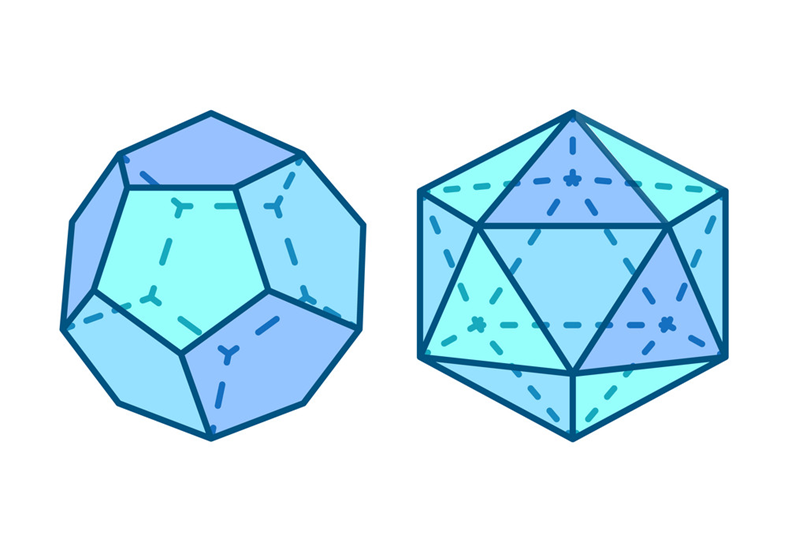
Fig. 12. Representation of a dodecahedron (left) and an icosahedron (right) (Robuart, n.d).

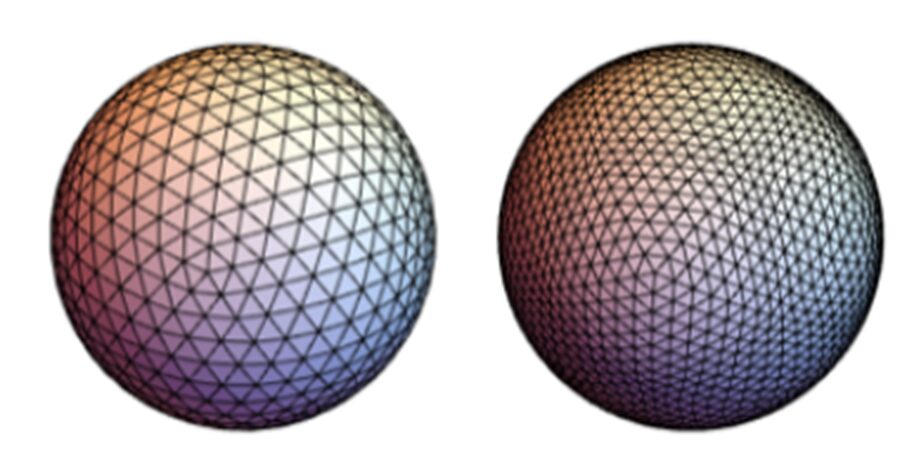
Fig. 13. Icosahedron-based sphere (left) and dodecahedron-based sphere (right), both at frequency k=4 (Beittenmiller, 2015).

As stated previously, geodesic spheres with an icosahedron or dodecahedron as the base polyhedrons have more uniformity in terms of the length and size of the triangles, however such perfect uniformity is not always present in the model, as well as in a biological system. Imperfections can occur during the growth mechanism of their internal structure (biomineralization), creating irregular regions. All in all, the geodesic sphere is not a definite model to represent the internal structures of certain radiolarians and other related species, but still an adequate start for a better understanding (Beittenmiller, 2015). A deeper understanding of biomineralization and the growth mechanisms of their silica structure is required to understand those irregularities, and to reflect them in a specific geometric model. To conclude, such models or similar geometric tessellations produce structural strength, for the minimal use of materials and energy.

Geometrical analysis of radiolarians by sub-micrometer X-ray tomography

Sub-micrometer X-ray tomography of radiolarians is used for skeletonization and computer modeling (Wagner et al., 2015). X-ray tomography is useful in the visualization of the surface and even the interior structure of the radiolarians. it is important to note that this high-resolution computerized tomography was done on fossilized radiolarians. Often, 3D imaging techniques are useful for investigating the phylogeny. In X-ray tomography, a tomographic series is acquired through the rotation of the X-ray source around the sample, then the intensity of the transmitted X-ray is recorded using multiple detectors. However, in sub-micrometer X-ray tomography, the specimen is rotating on a platform relative to the source-detector axis, while the source and detector remain fixed. Furthermore, it will operate on an adjustable voltage and power depending on each case. in this case, the machine operated at 50 kV and 0.7 W. Nevertheless, in these processes, the detectors obtain a set of images (x-ray projections) that are digitally assembled to be visualized and analyzed with a wide range of 3D imaging programs. The resolution of these images depends on many factors such as the X-ray intensity, the focal spot size of the X-ray source, the detector size, and the noise reduction. This type of tomography allows for sub-micrometer resolution. From these results, scientists were even able to print a 3D model of a radiolarian large to hold in the hand with a 3D printer that used a strong but flexible polymer (Fig. 15.). Furthermore, one is even able to digitally slice the model to see the intricate internal structural complexity of the medullary tests and the struts that hold them to the outer walls. Not only does this technique give the ability to identify the polygonal shapes of the radiolarian tests but also computes the many topological features of the tests like the length of the edges, the intersection of the edges at the nodes, and the number and coordination of the nodes (Fig. 14.).

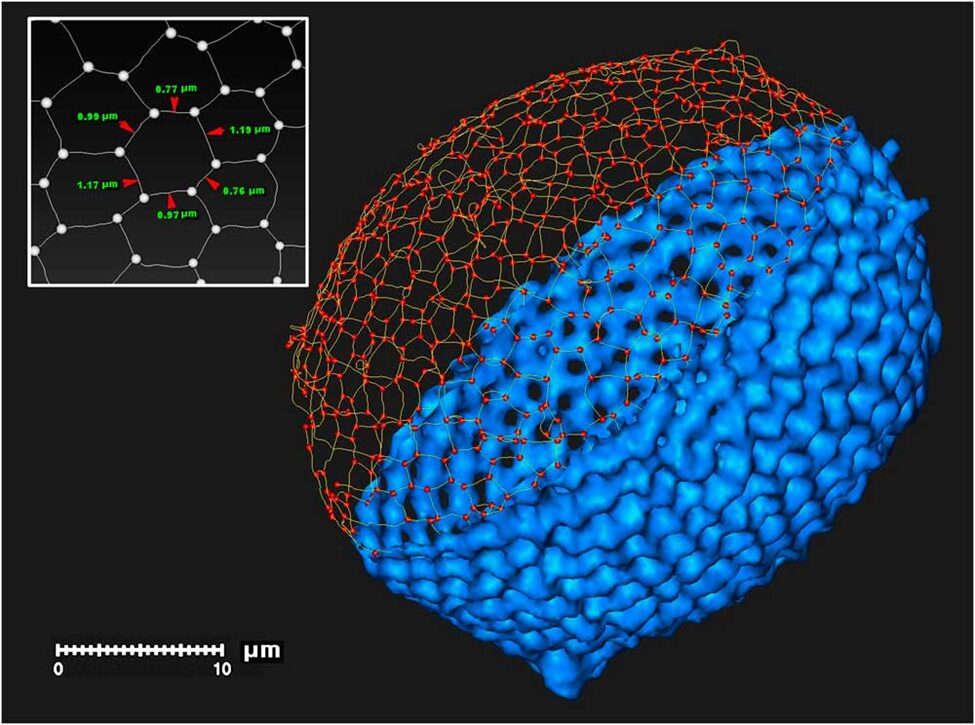
Fig. 14. Digital skeleton of a radiolarian test including polygonal segments and nodes (Wagner et al., 2015).

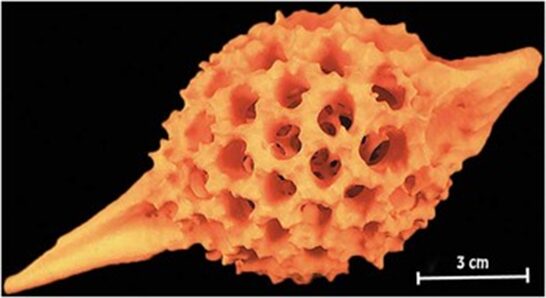
Fig. 15. 3D-printed model of radiolarian (Wagner et al., 2015).

Geometrical transformations of (some) Mesozoic radiolarians

Mesozoic radiolarians (the main groups being the nasselarians and the spumellarians) existed during the Mesozoic Era from around 252 to 66 million years ago. Throughout the years, the different types of radiolarian organisms have gone through geometrical transformations that were observed during various historical periods (Guex et al., 2012). One of the suspected reasons for the morphological changes in the organisms is the varying silica availability in sea waters. Radiolaria absorb silica from their surroundings to then form their shells. Thus, recent studies have demonstrated that a diminution of silica in ocean waters led to a much lighter radiolarian skeleton. However, no geometrical transformation of their shells was found. In other words, their geometry is independent of silica concentration.

Mesozoic radiolarians will rarely increase in size without shape distortion. For example, Cretaceous species such as Spongostichomitra and Obeliscoites. The Cretaceous Era ranged from 145 to 66 million years ago. Spongostichomitra has a conical to cylindrical test including extremely thick and unconstricted spongy walls (Guex et al., 2012). Obeliscoites is in a form of multisegmented and elongate. It is conical as well but wider.

Fig. 16. Demonstration of isometric size increase in the Cretaceous species Spongostichomitra (1) and Obeliscoites (2). Spherization of the test in the Palinandromeda (3), Mirifusus (4), and Thanarla (5)lineages (Guex et al., 2012).

Many species of Radiolaria go through spherization as they evolve over the course of their phylogeny. This process is represented in Palinandromeda, Mirifusus, and Thanarla (Fig.16) (Guex et al., 2012).

Palinandromeda is an amphipyndacid exhibiting a broad conical shape with 5 to 7 segments and a notable basal aperture. The cephalis is dome-shaped, lacks pores and typically features an apical horn. The thorax, a small cylindrical section, is directly linked to the cephalis (Guex et al., 2012). The abdominal and post abdominal segments take on a trapezoidal or bell-shaped form, which includes large pores that increase in size towards the distal end. The evolutionary trajectory of this group is defined by a shift towards a flatter abdominal segment, which led to the development of a planar basal surface. This evolutionary transformation represents an extreme exaggeration of the trend towards spherization, where the radius of the sphere becomes so large that the Nassellaria turns a widely bell-shaped and flat structure over its historical timeline.

Mirifusus is generally spindle-shaped during the Aalenian which began roughly 170 million years ago and lasted around 20 million years. During evolution, the test of Mirifusus showed a great increase in sphericity. It is very common for many species of this genus to become spindle-shaped and possible develop a terminal tube.

Furthermore, spherization can also be shown by the lineage Thanarla spoletoensis and Thanarla cucurbita in the mid-Cretaceous. They illustrate spindle-shaped test that seem to have inflated to exhibit a globose shape with a sharp pointed section and a conical section (Guex et al., 2012).

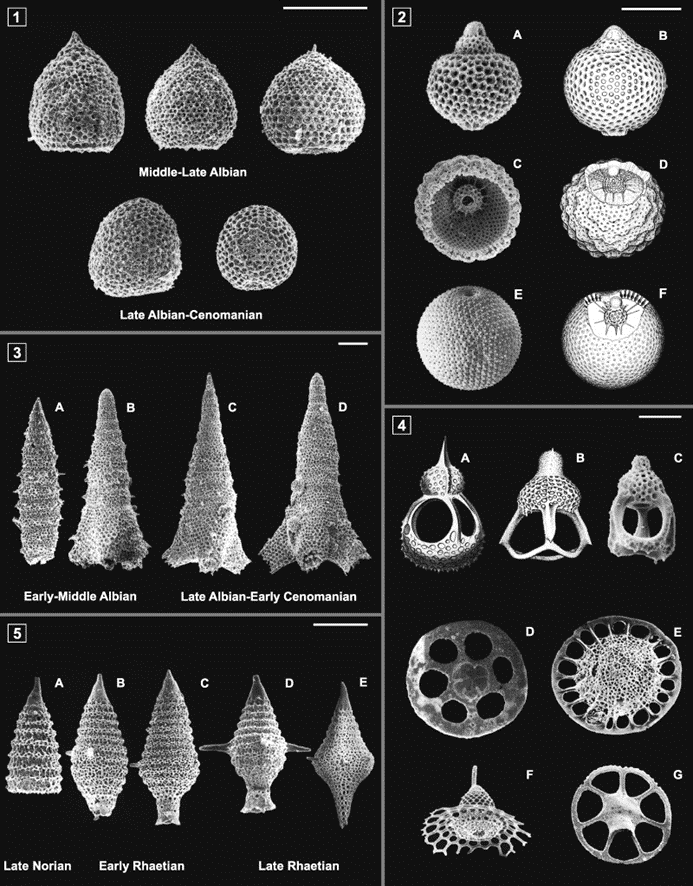
Fig. 17. Progressive morphological and geometrical changes on the skeletons of various radiolarians over historical periods (Guex et al., 2012).

There are many advantages to a spherical shape, in fact, it is the most economical skeletal shape. It has the smallest surface-to-volume ratio, hence, it minimizes exposure to external environmental factors like predators or strong currents. Additionally, its low surface-to-volume ratio is helpful in the stabilization of the radiolarian’s internal conditions (Guex et al., 2012).

Some species of Radiolaria (like the Spumellaria order) have spines that could reach ten times the diameter of their shells. These spines have modified geometrically over a long period and can be observed in the evolution of the Oertlispongidae and saturnalids. Originally, the middle Triassic Oertlispongidae were characterized by their spongy shells and their two polar spines. However, through time, the upper polar spines of these organisms transformed into a more intricate arc, indicating a connection between this group and the saturnalids. The evolution of saturnalids demonstrates the transformation of the spongy shell into a concentric arrangement of two medullary shells and one external (cortical) shell. Studies have determined how the saturnalids were derived from the Oertlispongidae through a parallel transformation of the opposite polar spine. This was succeeded by the lateral fusion of the two arcs, resulting in the distinctive, favorable equatorial ring characteristic of the saturnalids (Guex et al., 2012). Moreover, the genus Acanthotetrapaurinella (Fig.18 5(A-C)) in the Triassic period and the Acaeniotyle tribulosa Foreman (Fig.18 5(D-F)) in the mid-Cretaceous era experienced twisting of the spines.

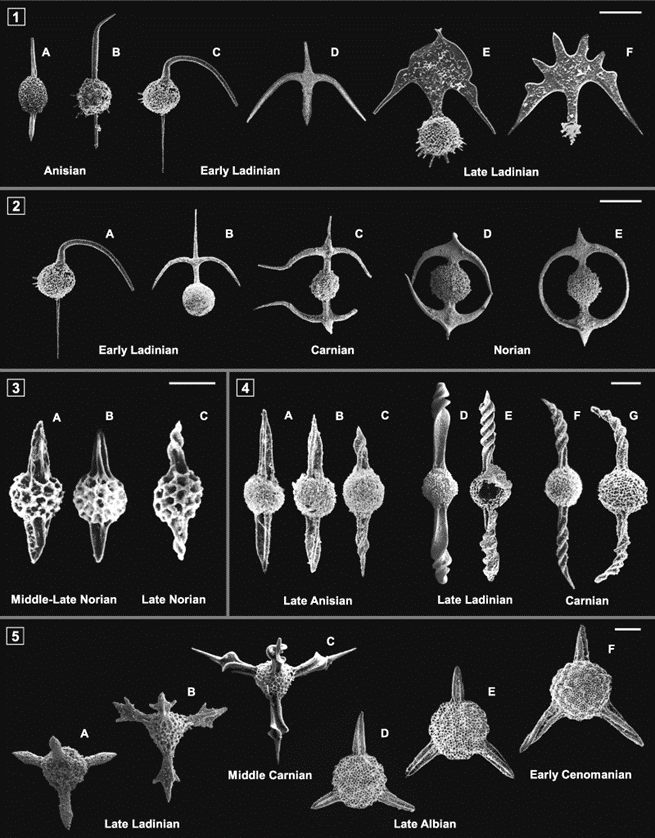
Fig. 18. Progressive geometrical modification of spines (Guex et al., 2012).

Radiolarians can face various sorts of external pressures such as temperature fluctuations, predation, pollution, nutrient availability, sedimentation, etc. In extreme cases, these tiny ocean organisms can lose their skeleton (Guex et al., 2012). Since this is such a significant simplification for the radiolarians, there are sometimes long gaps in fossil records where such small organisms seem to disappear and reappear later. What is incredible to see is the result of the skeleton’s disappearance. This event allows for a major structural reorganization of their bodies. One of the most noticeable changes in the reconstruction of their body shape is the change from a bilateral symmetry to a radial symmetry.

Conclusion

  In nature, energy conservation is maximized all the way down to the genetic code. Radiolaria’s symmetric structure allows for much more concise genetic instructions during development while minimizing the amount of materials used. Additionally, since Radiolaria primarily rely on drifting in ocean currents to move horizontally, having symmetries that are more dynamic in fluids makes this a more efficient transportation method. Radiolarian symmetry through evolution can be mapped by tracking the geometrical transformations in their phylogeny. As observed, there is a drastic trend towards spherization of tests across many radiolarian species, including when Radiolaria must rebuild its skeleton after extreme external stresses. Indeed, spherically symmetric tests present a single solution to many problems. The radial symmetry allows the organism to respond to its vast environment from all directions, which minimizes threat from external factors and maximizes predation. The low surface to volume ratio leads to enhanced internal stabilization. Further stabilization comes from the layers of near-equatorial triangles seen in spherical skeletons, as modeled by the geodesic sphere model. These triangular tessellation structures can withstand much more external pressure by distributing stress evenly, making it suitable for combating environmental changes, due to the minimal needs in materials and energy to biomineralize.

The study of Voronoi tessellations comprised of hexagons and pentagons provide an alternative model of spherical tests that can be explained using Euler’s theorem and graph theory. However, no skeletal model is perfect for every Radiolaria since nature is very complex. We can better understand geometric irregularities by studying biomineralization and the growth mechanisms of their silica structure. Specific skeletal shapes not only enhance radiolarian efficiency, but their balance between strength and inherent beauty are of great inspiration to both architecture and structural engineering.

References

Afanasieva, M. (2006). Radiolarian skeletons: Formation and morphology of skeletal shells.

Paleontological Journal, 40, 476-489.

Afanasieva, M. S., & Amon, E. O. (2014). Symmetry in radiolarian skeletons: Rules and

exceptions. Paleontological Journal, 48(11), 1163-1171.

https://doi.org/10.1134/S0031030114110021

Afanasieva, M., & Amon, E. (2003). A new classification of the Radiolaria.

Anderson, O. R. (2012). Radiolaria. Springer Science & Business Media.

Bellelli, F. (2023). The Fascinating World of Voronoi diagrams. Built In. https://builtin.com/data-science/voronoi-diagram

Beittenmiller, K. (2015). Characterizing the Geometry of Phaeodarian Colonial Spheres.

https://www.mbari.org/wp-content/uploads/2015/10/Beittenmiller_Katie.pdf

Britannica, T. Editors of Encyclopaedia (2021). symmetry. Encyclopedia Britannica.

https://www.britannica.com/science/symmetry-biology

Fortuna, S., & Savino, C. (2020). Symmetry, Asymmetry, Brain, and Sense Organs in Ancient Greek

Medicine. CONFINIA CEPHALALGICA, 30(2), 109-113.

Garvey, K. K. (2020). UC Davis Research: How Loss of Migration Affects Monarch Butterfly Wings

https://ucanr.edu/blogs/blogcore/postdetail.cfm?postnum=44087

Guex, J., O’Dogherty, L., Carter, E. S., Goričan, Š., Dumitrica, P., & Bartolini, A. (2012).

Geometrical transformations of selected Mesozoic radiolarians. Geobios, 45(6), 541-554.

Johnston, I. G., Dingle, K., Greenbury, S. F., Camargo, C. Q., Doye, J. P. K., Ahnert, S. E., & Louis, A. A. (2022). Symmetry and simplicity spontaneously emerge from the algorithmic nature of evolution. Proceedings of the National Academy of Sciences, 119(11), e2113883119. https://doi.org/doi:10.1073/pnas.2113883119

Jungck, J. R., Wagner, R., van Loo, D., Grossman, B., Khiripet, N., Khiripet, J., Khantuwan, W.,& Hagan, M. (2019). Art forms in nature: Radiolaria from Haeckel and Blaschka to 3D nanotomography, quantitative image analysis, evolution, and Contemporary Art. Theory in Biosciences, 138(1), 159–187. https://doi.org/10.1007/s12064-019-00289-z

Menger, K. (1931). New foundation of Euclidean geometry. American Journal of Mathematics, 53(4),

721-745.

Nielsen, N. (2016). What it Means to be Bilaterally Symmetrical.  Medium.

Robuart. (n.d). Dodecahedron and icosahedron vector image. In. VectorStock.

Voronoi, G. (1908). Nouvelles applications des paramètres continus à la théorie des formes quadratiques. premier Mémoire. sur quelques propriétés des formes quadratiques positives parfaites. Journal Für Die Reine Und Angewandte Mathematik (Crelles Journal), 1908(133), 97–102. https://doi.org/10.1515/crll.1908.133.97

Wagner, R. C., Jungck, J. R., & Van Loo, D. (2015). Sub-micrometer X-ray tomography of

radiolarians: Computer modeling and skeletonization. Microscopy Today, 23(5), 18-23.

Yoshino, T., Matsuoka, A., Kurihara, T., Ishida, N., Kishimoto, N., Kimoto, K., & Matsuura, S. (2012). Application of Voronoi Tessellation of Spherical Surface to Geometrical Models of Skeleton Forms of Spherical Radiolaria.