Exploring the Mathematics of Unicellular Green Algae (Chlamydomonas Reinhardtii)
Ai-Lan Ji-Eun Nguyen, Tesnim Obey, Anders Schwarz, Jackson Yu
Abstract
Mathematics could be described as an area of knowledge involving the use of numbers, equations, and models to describe phenomena, but at its essence, mathematics is the language of the universe. Accordingly, every aspect of the natural world is governed by this “language,” and with each passing day, humanity draws itself closer to achieving fluency. Mathematics is perhaps the best way to describe the intricate tapestry of biology and the natural world, capable of revealing mechanisms behind a variety of aspects. This essay will delve into the elegant mathematics underlying mainly the structure, movement, and growth of the unicellular green algae Chlamydomonas. This will be achieved by utilizing mathematical tools including geometry and differential equations to analyze flagellar beating in phototaxis, mathematical modeling techniques to describe the body proportions and metabolism, and additional iterative modeling methods to express the changing population sizes. Through a synthesis of these mathematical methods, a deeper understanding will be reached of this model organism serving as a testament to nature’s ingenuity.
Introduction
Chlamydomonas is a genus of unicellular green algae over a billion years old, having withstood the test of time. Today it is considered a model organism for possessing a variety of unique characteristics or ‘design solutions’ that have enabled it to survive and thrive across a wide range of habitats since almost the beginning of life itself, and some of these characteristics have been previously analyzed from a physical and chemical standpoint. Yet, both standpoints ultimately fall under the boundless umbrella of the field of mathematics itself, the language of the universe. While mathematics may fundamentally describe all fields of science, it can be seen more explicitly in particular aspects of nature, from the Fibonacci sequence dimensions of flower petals and nautilus shells to perfectly shaped hexagonal honeycombs to fractal patterns of tree branches, it can even be visually deduced without much thought that the natural world adheres to mathematical reality.
However, mathematics can be utilized by scientists to see deeper than simple patterns and describe more complex phenomena from motion to thermodynamics to metabolism to describing complex population dynamics. Firstly, the flagellar beating of Chlamydomonas will be deeply analyzed using concepts like waveform analysis and fluid dynamics to reveal what exactly makes this process worthy of gifting the term “model organism” to Chlamydomonas, before exploring optimization theory and scaling laws to determine how nature strikes an optimal balance between size, energy consumption, and resource utilization. Lastly, population dynamics will be investigated using a variety of models including iterative models. This exploration brings us full circle, connecting the intricacies of flagellar beating and metabolic and scaling efficiency to the grand tapestry of population dynamics – a testament to the interconnectedness of mathematical principles woven into the very fabric of nature’s design solutions.
Modelling of the cell structure
The modelling of a 3D picture for the unicellular green algae (Chlamydomonas) consists of three beads interacting with the surrounding fluid, and the body of the green algae. The cell body is a sphere of radius a0 located at r0. Surrounding this, we have two beads, each with a radius significantly smaller than that of the main body, positioned at the drag centers of the flagella, labeled as r1 and r2. These beads, symbolizing the flagella, are influenced by changing tangential forces Fi(t), for i equals 1 and 2, and their movement is restricted to circular paths with a consistent radius R. Forces perpendicular to this path, Fi(n), ensure the motion emulates the swimming style of breaststroke. All three beads in the model are affixed to a stable triangular frame that aligns with the reference frame of the body, as depicted in Figure 1. This frame has two key dimensions, labeled ℓ and h, where the radius of the beads is much less than the radius of the body, which is in turn significantly less than both ℓ and h. The rationale behind this design stems from experimental findings indicating that the fluid dynamics around Chlamydomonas cells, propelling themselves freely, can be effectively summarized by a mere trio of point forces, known as Stokeslets (Drescher et al., 2010). Simplified versions of this model have successfully captured the random but coordinated behavior characteristic of the dual flagella’s motion (Lushi, Kantsler, & Goldstein, 2017). These essential depictions of the ciliary motion, with beads tracing specific orbits, serve as invaluable instruments for delving into hydrodynamic synchronization studies (Brumley et al., 2012).
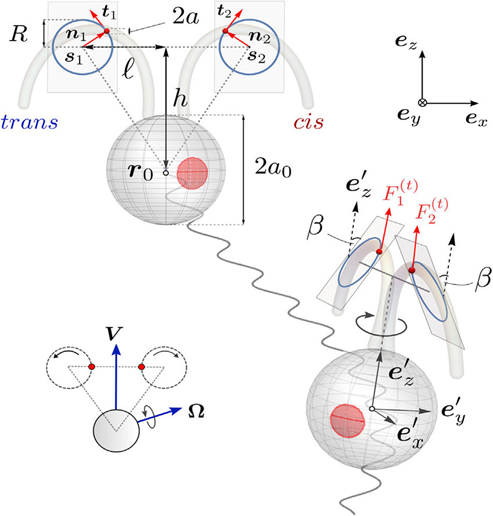
Fig. 1. A comprehensive three-dimensional representation of a Chlamydomonas cell in motion, captured from both frontal and lateral perspectives. The motion of the cell’s flagella is simulated using petite beads that are restricted to move in circular paths within dual inclined planes of beating, offering a true-to-life scaffold structure as seen in the inset. The reference frames for the body and the laboratory are denoted by the sets ex‘, ey‘, ez‘ and ex, ey, ez, respectively (Cortese & Wan, 2021).
Flagellar synchronization and coordination
The intricate dance of cilia and flagella, essential for the propulsion and maneuvering of a myriad of microscopic organisms, has long intrigued scientists. These slender organelles beat with a precision that belies the complex coordination required, particularly when their synchronized movement is essential for biological processes. Whether it is the cilia in the fallopian tube orchestrating the passage of an egg or the flagella of sperm swimming in unison, the underlying mechanism of this synchrony is a fascinating interplay between biophysics and environmental interaction. Researchers have postulated that the fluid dynamics surrounding these organelles play a crucial role, with experiments and mathematical models supporting the notion that the fluid’s movement itself can induce synchronization. Intriguingly, even when physically separated and devoid of any direct communication, flagella have demonstrated the ability to sync their beats, a testament to the subtle yet powerful influence of their shared watery domain. This phenomenon is not just a quirk of nature but has profound implications for our understanding of cellular processes and the potential harnessing of such mechanisms in biomedical engineering and nanotechnology.
The study of the fluid dynamics generated by a single flagellum has revealed some interesting insights. While a flagellum is complex in its structure and internal dynamics, the flow fields it creates can be simplified for certain scales. In simpler models (Vilfan & Jülicher, 2006), such as those used for studying synchronization, a single sphere moving along a fixed path in space, driven by internal forces, is often used to represent the flagellum. This approach approximates the time-averaged flow around the flagellum to that produced by a point force at an average location.
When a force F acts on a viscous fluid at a point x0, it creates a velocity field called a Stokeslet. This was described by:
u_i=F_j/8πμr (δ_{ij}+(r_i r_j)/r^2 )(1)
where the vector r = x – x0, r = |r|, and δij is the Kronecker delta. The time-averaged flow field around freely swimming Chlamydomonas cells matches in magnitude and topology with a three-Stokeslet model, which includes one Stokeslet for each flagellum and one for the cell body (Drescher et al., 2010).
Figure 2A illustrates the flow field around a solitary cell in various instances, vividly depicted through changes in color intensity and vector direction that correspond to the flagellum’s distinct power and recovery strokes during its beat cycle. When we consider the velocity field averaged over time, derived from data aggregated across four cells (as seen in Figure 2B), it becomes evident that beyond a threshold of 20 micrometers from the extremity of the flagellum, the flow in both the approaching and receding directions adheres to the decay pattern characteristic of a Stokeslet (u approximately proportional to 1/r), detailed in Figure 2C. Notably, this pattern persists across the spatial range relevant to the experiments involving pairs of cells.
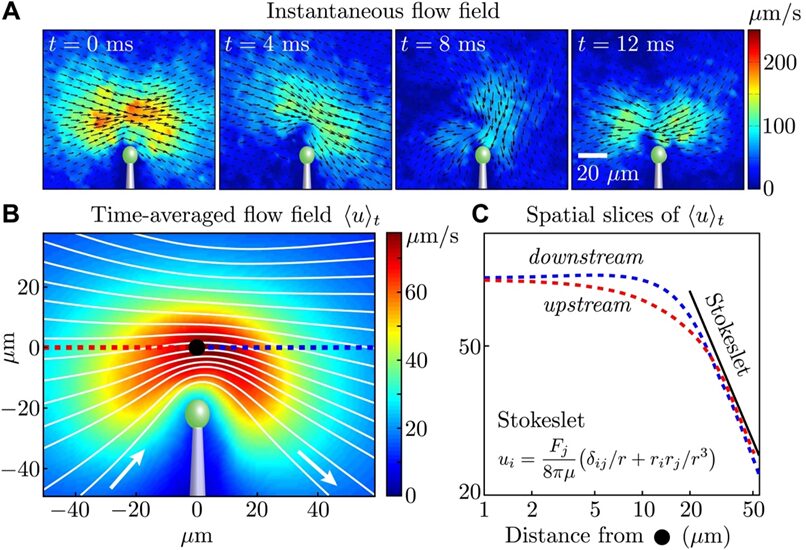
Fig. 2. (A) The flow field around a single cell, captured at different moments within the first portion of the flagellar beat cycle, is measured using particle image velocimetry. (B) The composite flow field over time, ❬u❭t is calculated by integrating the absolute velocity |u(x, t)| over the duration τ, which spans approximately 1000 beats, and averaging this across four cells. This is visualized through varying intensities of color to represent velocity magnitude and white lines to indicate streamlines. (C) The flow’s velocity magnitude, shown in red for the flow moving toward the cell and in blue for the flow moving away, is depicted relative to a fixed point marked by a black dot in panel B (Brumley et al., 2014).
The fluid flows generated by flagella, far from being chaotic, exhibit a remarkable level of order, guided by the laws of hydrodynamics. This order becomes evident when analyzing the flagellar motion over time, where the collective dynamics reveal a persistent and underlying rhythm. The transition from individual beat cycles to a consistent and synchronized pattern across multiple cells speaks volumes about the implicit communication through the fluid medium. The streamlines and velocity fields, beautifully captured and quantified using particle image velocimetry, lay bare the invisible forces that bind these microscale swimmers into a synchronized entity. This seamless integration of motion, where physical proximity translates into rhythmic concord, highlights the fluid medium not as a mere bystander but as an active participant in the coordination of biological processes.
The research into flagellar synchronization and coordination underscores the pivotal role of hydrodynamic forces in mediating this complex biological dance. Even in the absence of chemical signals or mechanical connections, flagella can achieve an intricate state of harmony, locking into synchronized patterns for extended periods. This synchronization is not just an isolated phenomenon but is accompanied by a notable adjustment in the flagellar waveform, suggesting a deep-rooted interplay between form and function. The consistency of these observations with hydrodynamic theory, across different species and cellular conditions, points to a fundamental principle of fluid dynamics at play in biological systems. The findings from these meticulous studies, particularly with model organisms like Chlamydomonas, not only validate existing theoretical models but also pave the way for new insights into the universal principles governing cellular motility and coordination.
Cellular size optimization
The limits governing cell size appear to be linked to the optimal cell-to-volume ratio, a critical factor in facilitating efficient extracellular interactions. This ratio plays a pivotal role as it dictates the availability of surface area crucial for pivotal cellular activities such as exocytosis, endocytosis, and the positioning of protein channels, regulating vital ion fluxes. Moreover, within Chlamydomonas, the survival and intracellular content seem proportional to the number of encoding genes, which is a reflection of nucleus size. And so, synthesis relies on intracellular interactions in the cytoplasm which mostly acquire the necessary substrates through extracellular reaction. Through the study of mature Chlamydomonas in optimal conditions, the relationships between the cytoplasm, the nucleus size, and the surface area can be explored (Morris, 2002)
The nucleocytoplasmic ratio (N:C), the ratio between the nucleus size and cytoplasm, as shown in Figure 3, underscores the necessity for sufficient cellular space to enable the expression of genetic coding within the cell, thereby ensuring its functionality. However, there emerges a pattern where the synthesis of a certain cellular component decreases or stops once the amount of it produced can sustain homeostasis (Umen, 2005). This can be due to energy conservation, as additional material would, at best, not be used or at worst hinder the balance created (Hershey et al., 2012). Once again, synthesis relies on the components that enter the cell through the membrane.
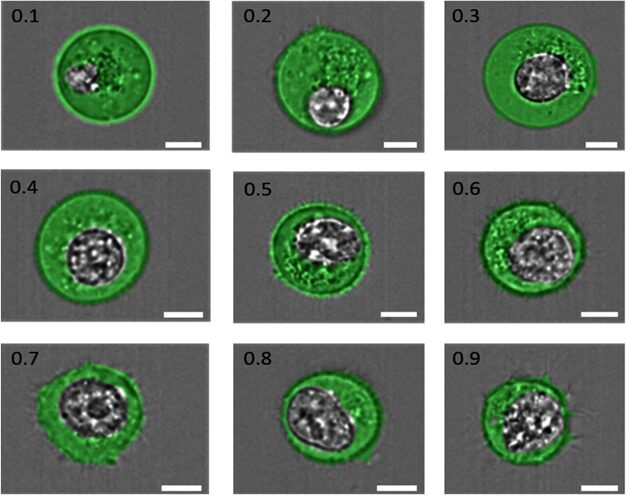
Fig. 3. “Examples of cells having N:C ratios ranging from 0.1 to 0.9, as indicated in the top left corner of each image. The cell cytoplasm has been pseudo-colored green, and the nucleus is shown in grayscale. The scale bar in each image is 7 μm” (Moore et al., 2019).
It can then be deduced that there exists an optimization mechanism within the cell that maximizes the membrane’s surface area while restricting intracellular content. This balance is calibrated such that the ‘amount’ of cellular content—be it measured in mass, moles, volume, or other metrics—is precisely tailored to fulfill the essential functions required for the system’s survival and a larger surface area allows for more efficient exchange of materials with the surrounding environment. Curiously, the almost spherical shape of the Chlamydomonas cell as well as many other eukaryotic cells maximizes the surface area to volume ratio (Seidenberg, 1988). This can be explained by the medium that Chlamydomonas lives in; as described in the physics paper, its ellipsoidal shape allows for more efficient movement in water.
Curiously, N:C ratios remain relatively constant between different Chlamydomonas cells (Moore, 2019), despite their variation in size (Figure 4).
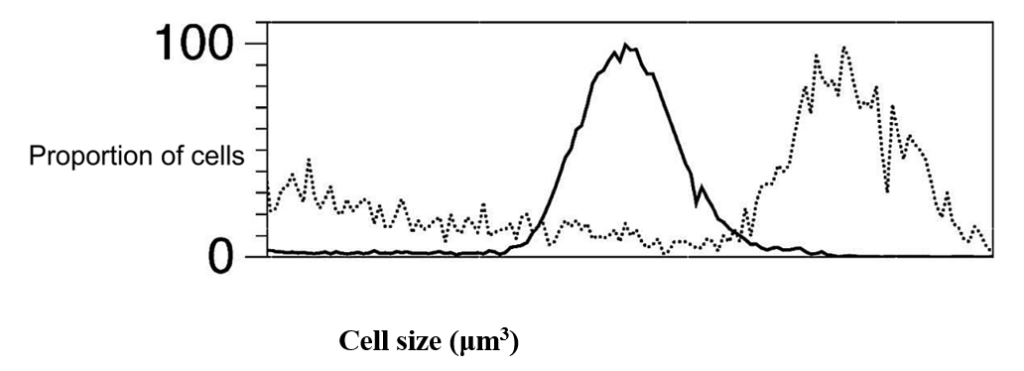
Fig. 4. Size distribution of daughter cells (solid black line) and pre-division mother [mature] (dashed lines) Chlamydomonas cells grown in the same environment (Olson et al., 2010).
This ratio serves as a guiding principle rather than an absolute determinant of cell size, as it is questioned whether Chlamydomonas perceives its size or if it relies on reaching an equilibrium point to begin cell division (Olson et al., 2010). Thus far, the N:C ratio functions more as a starting point to study cell size regulation in Chlamydomonas and possibly in other eukaryotic cells. Theoretically, the consistency of the ratio largely relies on exocytosis and endocytosis (Tuxhorn et al., 1998). These mechanisms allow for the maintenance of a steady state by ensuring that the “amount” of cellular content remains relatively constant despite the ongoing changes that ensure the cell’s survival. Exocytosis involves the formation of vesicles derived from the cellular membrane, which then exit the cell, effectively reducing the cellular content and the membrane surface area. Conversely, endocytosis encompasses the fusion of vesicles with the cellular membrane, thereby augmenting the cell’s content and surface area.
Mathematically, these dynamics can be represented by balance equations encapsulating the biochemical reactions within the cell. In a mature cell in homeostasis, the “content” of the cell does not change, and it can be denoted by
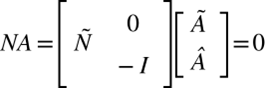
(2)
NA concerns the rates of change of various species within the system, that is the Chlamydomonas cell. The stoichiometric matrix, Ñ intertwined with the internal flux subvector Ã, reflects the flow rates of compounds within the system. The boundary flux subvector Â, reflecting the rates of exchangeable compounds at the cell’s membrane, plays a pivotal role in dictating the exchange rates of these compounds. Each element in this matrix, at the ith row and jth column, represents the stoichiometric coefficient of species i in reaction j. These coefficients are positive if species i is a product of the reaction and negative if i is a substrate, i.e. something that’s consumed in the reaction. (2) describes that the overall change of the cell content is null as what is leaving the cell, entering it, being transformed, or being produced balances out at the cellular scale. In other words, there is an equilibrium in the system. Previously, it was established that the cytoplasm volume remains constant overall and that the optimal surface area to volume ratio should remain constant for mature Chlamydomonas. So, by assuming that the “content” inside the cells stays constant through dynamic change (NA=0) and that this change (or boundary flux Â) at the boundary is done by exocytosis where the vesicle is formed by the membrane and leaves the cell with cell content, reducing the surface area and endocytosis in which the vesicles fuse in the membrane to increase the cell content, it can be assumed that there is no change in the surface area “M” (Wemmer & Marshall, 2007). This can be denoted as:
dM/dt = 0
(3)
Where the rate of change of the surface area over time is null.
If we further assume the rate of vesicle budding from the surface is proportional to the surface area, we immediately obtain a simple balance‐point model for size control. By setting the variable for the rate of vesicle fusion as a and the rate of vesicle budding as proportional to the surface area (βM) If we let the rate of vesicle fusion onto the surface be represented by the variable α, and the rate of budding be equal to βS, then the instantaneous rate of change of the surface area M is given by,
dM/dt = α − βM =0
(4)
The surface area depending on time is:
M=C/e^{βt} +α/β(5)
Finding the equilibrium solution M = α/β by letting the time approach infinity indicates that the surface area will remain constant as the rate of vesicle fusion must balance the rate of vesicle budding scaled to the surface area, emphasizing the relationship between cellular dynamics, surface area optimization, and the maintenance of cellular content and surface area within the realm of Chlamydomonas.
Effects of light
Using model (2) in Chlamydomonas, the changes in the cell during increases in light photon flux, or the number of photons that reach the cell over a period, can be further analysed. In fact, it is shown that an increase in photon flux corresponds to an increase in cell mass, contradicting the presumed stability in cellular content and the surface area to volume ratio in (3) (Cogne et al., 2011). This indicates that light might be a limiting factor in cellular growth. Strikingly, organelles within the cell exhibit negligible changes in mass even as the cell grows, while the ratio of lipid, carbohydrate, and starch content mass to total cell mass ratio (or mass fraction) increases as shown in Figure 5.
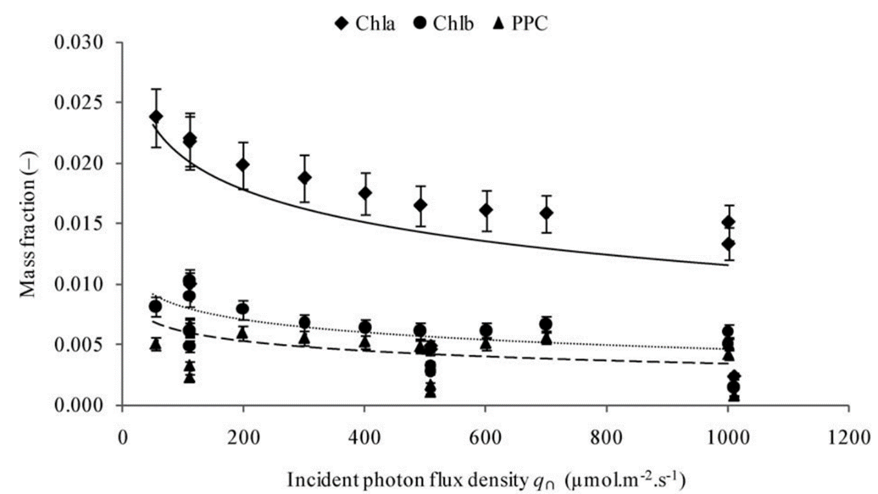
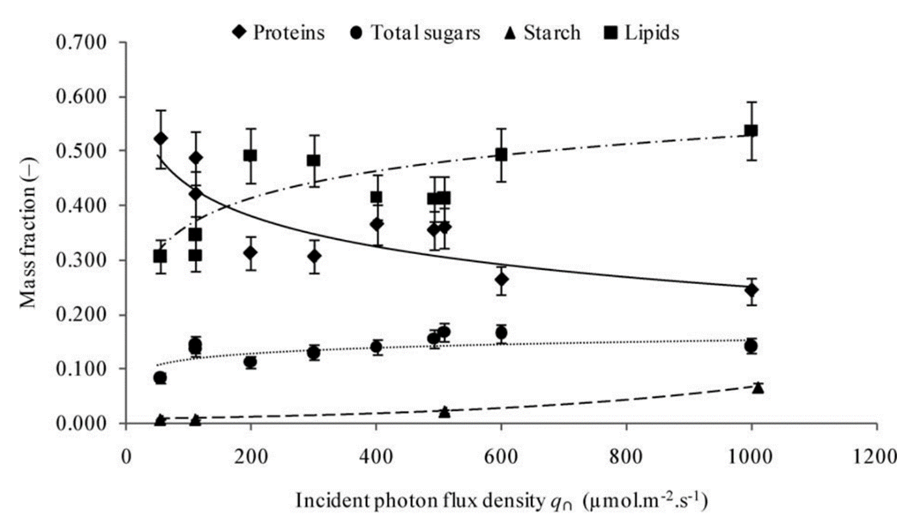
Fig. 5. Evolution of the mass fractions of components into biomass as a function of the incident photon flux density with Chl being chlorophyll and PPC being photoprotective carotenoids (Cogne, 2011).
Remarkably, the proportion of starch content experiences a seemingly exponential increase whereas the total sugar mass and lipids increase logarithmically. This discrepancy, while challenging established equilibrium models, holds immense potential, particularly in the context of biologically derived substance production. Furthermore, the increase in fat content would prove useful for optimizing the extraction of biofuel from Chlamydomonas.
Flagellar length control
While the models presented in equations 3 and 4 are useful in analysing the limitations and the growth of Chlamydomonas reinhardtii, they might be inconsistent in certain regulatory processes such as intraflagellar transport (as explored in a previous paper. Using the discussed models which simply equalize the cell’s inputs through cellular transport does not explain the flagella length regulation. In fact, if the flagellar length were to be randomized, the distribution of length in the population would follow a negative exponential curve, where most cells would have short flagella while a few would have longer ones (Verde et al., 1997). However, what is seen is a Gaussian distribution, where the flagellar length is regular across several cells averaging at around 10-14 micrometers with a standard deviation of 1 micrometer (Wheatley and Bowser, 2000). This tight distribution contrasts with what would be expected without a control system and by simply using the previous mathematical models. Further observations reveal that, while the flagella between cells may differ, the two flagella within a single cell remain more similar to each other. This suggests an additional mechanism for equalizing lengths within a cell and indicates that variations in a population might stem more from cell-to-cell differences rather than fluctuations within the length control system (Wemmer et al., 2007). And so, while the mathematical models presented were useful in exploring cell content distribution and the regulation of the cell body, the precise mechanisms governing flagellar length control in Chlamydomonas emphasised the need for nuanced models that consider the intricate dynamics of cell and organelle growth.
Population growth in chlamydomonas
The dynamics of Chlamydomonas reinhardtii populations can be observed and projected using basic mathematical models, though the actual dynamics are typically influenced by numerous factors not considered in these simplified equations. Experimental data must be incorporated when creating more realistic models, to refine equations based on specific observations and conditions.
Reproductive habits of chlamydomonas
As unicellular green algae, Chlamydomonas reinhardtii exhibits both sexual and asexual modes of reproduction (Atzori et al., 2021). The distinction between these reproductive strategies is influenced by environmental conditions as well as the availability of resources (Atzori et al., 2021).
The most common form of asexual reproduction in Chlamydomonas is binary fission (Cross & Umen, 2015). Chlamydomonas, along with other green algae, can reproduce through a multiple-fission cell cycle, or palintomy, which is denoted by a prolonged growth phase through which cells can nearly double in size (Cross & Umen, 2015). During binary fission, the parent cell divides into two daughter cells, or zoospores, each genetically identical to the parent cell (Cross & Umen, 2015). This process is rapid and efficient, which allows Chlamydomonas to quickly increase its population under favourable conditions.
Along with binary fission, Chlamydomonas is also capable of isogamous sexual reproduction (El-Bawab, 2020). During this process, a cell goes through mitosis for two or more rounds, thus producing nearly 64 new cells (El-Bawab, 2020). As these resulting cells do not develop cell walls, they become morphologically similar, but physiologically different gametes (El-Bawab, 2020) MT+ and MT–; when a compatible pair of these flagellated gametes meet, they fuse to form a zygote (Lin & Goodenough, 2007). Under certain environmental conditions, Chlamydomonas can also undergo conjugation, which is a process where two cells come into close contact and a cytoplasmic bridge forms between them. Genetic material is then exchanged through this bridge, which leads to the formation of recombinant zygotes (Sodeinde & Kindle, 1993).
As previously mentioned, there are various external factors that play a part in determining reproductive modes utilized by Chlamydomonas reinhardtii. One such factor is the availability of nutrients within the environment (El-Bawab, 2020). Asexual reproduction through binary fission is a rapid way to exploit favorable nutrient conditions when resources are abundant (El-Bawab, 2020).
Under conditions of nutrient limitation or stress, sexual reproduction may allow for the creation of genetic diversity, which could potentially lead to offspring with increased adaptability to changing environmental conditions (Lin & Goodenough, 2007). Another factor that favours sexual reproduction over asexual reproduction is population density (Lin & Goodenough, 2007). High population density allows for the encounter of diverse mating types, thus promoting genetic recombination (Lin & Goodenough, 2007).
Modelling population growth
There are diverse methods of modelling the growth of a given population. For instance, a simple Reproduction Rate Model can be considered to model the reproductive habits of Chlamydomonas reinhardtii:
dR/dt=βR
(6)
where dR/dt represents the rate of reproduction (R) over time (t), and β represents the reproductive rate (Hasan & Ness, 2020).
The Logistic Growth Model is commonly used to describe the growth of a species’ population when it has limited resources (Borlestean et al., 2015). As such, to potentially model the growth of a Chlamydomonas population under limited nutrient conditions (and thus undergoing sexual reproduction), the following Logistic Equation can be employed:
dN/dt=rN(1-N/K)
(7)
where dN/dt is the rate of the population’s growth over time (t), r is the intrinsic growth rate of the population, N is the population size, and K is the carrying capacity that represents the maximum sustainable population size (Borlestean et al., 2015).
Modelling cell growth
While the Logistic Growth Model is a more generalized method of describing the growth of a population given limited resources, M. R. Droop developed a model specifically targeted at analyzing the growth of individual algal cells under nutrient limitation (Droop, 1973). Droop’s model makes distinctions between the external substrate concentration S and the internal substrate Sic (representing the substrate absorbed by the algae cells) (Droop, 1973). This model falls notably under the category of biological models designed to describe cellular growth by considering the biomass within the system (Atzori et al., 2021). Droop defines the cell quota, q, by considering internal substrate with respect to the biomass concentration, b:
q=S_{ic}/b(8)
As per the Droop model, the growth process of algae cells is governed by the uptake of external substrate as well as the biological conversion of internal substrate into biomass (Droop, 1973). By calculating the time derivative of cell quota, q, it must be noted that the uptake of a substrate, S, is equivalent to the generation rate for internal substrate Sic, as a consequence of the conservation of mass (Droop, 1973).
It is important to acknowledge a key limitation of the Droop Model, which is that it does not fully address a crucial aspect of biological systems (Atzori et al., 2021). Cell properties, like cellular mass, are distributed among the cell population due to the division process (Atzori et al., 2021). As such, the system is characterized by a distribution of cells across the mass domain at any given moment (Atzori et al., 2021). This underplays the complexity involved in modelling cellular growth processes and the need to consider the distribution of cell properties within a population (Atzori et al., 2021). The Droop model also fails to consider stochastic effects, which are random or unpredictable variations in the system (Atzori et al., 2021).
To formulate a mathematical model capable of elucidating this phenomenon, Mantzaris and Daoutidis present alternative population models (Mantzaris & Daoutidis, 2004). They introduce a novel physical parameter denoted as n(m,t) which corresponds to the distribution of cell mass, and denotes the count of cells with a mass within a given interval [m, m+dm], at a certain time, t, expressed per unit volume (Mantzaris & Daoutidis, 2004)). Using the previously mentioned variables, Mantzaris and Doautidis have developed a Cell Distribution Balance Equation for algae cell growth within a batch reactor:
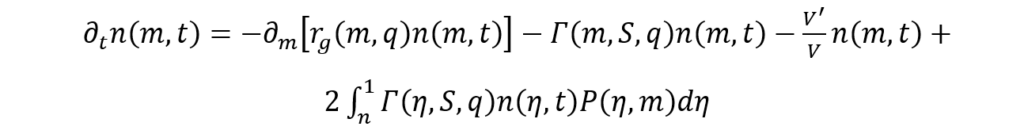
(9)
where V is the reactor volume.
The term ∂tn(m, t) is meant to account for the time dynamics involved in cell distribution (Mantzaris & Daoutidis, 2004). Meanwhile, the right-hand side of the above equation is comprised of a growth term (1st term) describing cell mass variation throughout the growth process, the division term (2nd term) which represents the loss of cells, of mass m, caused by their division into cells of smaller mass (Mantzaris & Daoutidis, 2004). The last term on the right-hand side is the birth term, which arises as a result of the production of cells of mass, m, due to the division of larger-mass cells (Mantzaris & Daoutidis, 2004). This birth term in the Cell Distribution Balance Equation also makes sure to account for the variation of volume in time (Mantzaris & Daoutidis, 2004).
The above equations are designed to capture the complex interplay between cell growth and the temporal evolution of cell distribution, thus providing a comprehensive framework for understanding biological processes (Atzori et al., 2021).
Manipulating chlamydomonas growth for engineering applications
Understanding the interaction between environmental factors and reproduction can help researchers effectively predict and manipulate the reproductive modes of Chlamydomonas reinhardtii, which can be valuable for various applications (Yang et al., 2018). For instance, the utilization of individual nutrient depletion is commonly employed in order to stimulate biomass accumulation, such as lipids, in microalgae such as Chlamydomonas (Yang et al., 2018). However, this approach often leads to cell growth inhibition and a reduction in total biomass (Yang et al., 2018). Therefore, enhancing lipid accumulation in nutrient-deficient cells without compromising biomass presents a promising, and cost-effective, strategy for the production of more economical biofuels (Yang et al., 2018). This process was made possible by researchers being able to understand and model the growth behaviours of Chlamydomonas cells given various environmental changes, such as nutrient depletion, and then projecting these results to know how to effectively manipulate the process for practical applications (Yang et al., 2018).
Conclusion
Chlamydomonas’ optimization of its cell body appears to revolve around an intricate balance of cellular dynamics, specifically geared toward maintaining an optimal membrane-to-volume ratio and nucleus-to-cytoplasm (or volume) ratio. This ratio enables efficient extracellular interactions necessary for crucial cellular activities such as exocytosis, endocytosis, and ion flux regulation by maximizing the surface area of the membrane while keeping enough space in the cell for metabolic processes to occur. There is also the nucleocytoplasmic ratio, which ensures that there is enough space in the cytoplasm to process and express the genetic coding which roughly indicates nucleus size.
Furthermore, the alga responds to diverse environmental cues and resource availability and adjusts its reproductive strategies for maximum population growth. It exhibits adaptability through a spectrum of reproductive modes: binary fission for rapid proliferation under favorable conditions, and sexual reproduction in response to nutrient limitations or stress, fostering genetic diversity for environmental adaptability. This switch between sexual and asexual reproduction allows for the proliferation and survival of the species under extreme conditions while allowing the species to adapt to the environment over time through the increase of genetic variability.
Chlamydomonas reindhartii, despite its microscopic size and ancient origins, became a beacon that shines light onto the complexities of life offering a deeper understanding of the world’s intricacies. Its contributions to science serve as a testament to the depth and richness of biological inquiry and continue to inspire future investigations into the intricate chemical, physical, and finally mathematical mechanisms that govern life.
References
Atzori, F., Jerono, P., Schaum, A., Baratti, R., Tronci, S., & Meurer, T. (2021). Identification of a cell population model for algae growth processes⁎⁎ IFAC-PapersOnLine, 54(7), 132-137. https://doi.org/https://doi.org/10.1016/j.ifacol.2021.08.347
Borlestean, A., Frost, P. C., & Murray, D. L. (2015). A mechanistic analysis of density dependence in algal population dynamics [Original Research]. Frontiers in Ecology and Evolution, 3. https://doi.org/10.3389/fevo.2015.00037
Brumley, D. R., Wan, K. Y., Polin, M., & Goldstein, R. E. (2014). Flagellar synchronization through direct hydrodynamic interactions. elife, 3, e02750.
Cogne, G., Rügen, M., Bockmayr, A., Titica, M., Dussap, C.-G., Cornet, J.-F., & Legrand, J. (2011). A model-based method for investigating bioenergetic processes in autotrophically growing eukaryotic microalgae: Application to the green algae Chlamydomonas reinhardtii. Biotechnology Progress, 27(3), 631-640. https://doi.org/https://doi.org/10.1002/btpr.596
Cortese, D., & Wan, K. Y. (2021). Control of helical navigation by three-dimensional flagellar beating. Physical Review Letters, 126(8), 088003.
Cross, F. R., & Umen, J. G. (2015). The Chlamydomonas cell cycle. Plant J, 82(3), 370-392. https://doi.org/10.1111/tpj.12795
de Carpentier, F., Lemaire, S. D., & Danon, A. (2019). When Unity Is Strength: The Strategies Used by Chlamydomonas to Survive Environmental Stresses. Cells, 8(11), 1307. https://www.mdpi.com/2073-4409/8/11/1307
Drescher, K., Goldstein, R. E., Michel, N., Polin, M., & Tuval, I. (2010). Direct measurement of the flow field around swimming microorganisms. Physical Review Letters, 105(16), 168101.
Droop, M. R. (1973). Some thoughts on nutrient limitation in algae 1. Journal of phycology, 9(3), 264-272.
El-Bawab, F. (2020). Chapter 3 – Phylum Protozoa. In F. El-Bawab (Ed.), Invertebrate Embryology and Reproduction (pp. 68-102). Academic Press. https://doi.org/https://doi.org/10.1016/B978-0-12-814114-4.00003-5
Hasan, A. R., & Ness, R. W. (2020). Recombination Rate Variation and Infrequent Sex Influence Genetic Diversity in Chlamydomonas reinhardtii. Genome Biol Evol, 12(4), 370-380. https://doi.org/10.1093/gbe/evaa057
Hershey, J. W., Sonenberg, N., & Mathews, M. B. (2012). Principles of translational control: an overview. Cold Spring Harb Perspect Biol, 4(12). https://doi.org/10.1101/cshperspect.a011528
Lin, H., & Goodenough, U. W. (2007). Gametogenesis in the Chlamydomonas reinhardtii minus mating type is controlled by two genes, MID and MTD1. Genetics, 176(2), 913-925. https://doi.org/10.1534/genetics.106.066167
Lushi, E., Kantsler, V., & Goldstein, R. E. (2017). Scattering of biflagellate microswimmers from surfaces. Physical Review E, 96(2), 023102.
Mantzaris, N. V., & Daoutidis, P. (2004). Cell population balance modeling and control in continuous bioreactors. Journal of Process Control, 14(7), 775-784.
Moore, M. J., Sebastian, J. A., & Kolios, M. C. (2019). Determination of cell nucleus-to-cytoplasmic ratio using imaging flow cytometry and a combined ultrasound and photoacoustic technique: a comparison study. J Biomed Opt, 24(10), 1-10. https://doi.org/10.1117/1.Jbo.24.10.106502
Morris, C. E. (2002). How did cells get their size? The Anatomical Record, 268(3), 239-251. https://doi.org/https://doi.org/10.1002/ar.10158
Ness, R. W., Morgan, A. D., Colegrave, N., & Keightley, P. D. (2012). Estimate of the spontaneous mutation rate in Chlamydomonas reinhardtii. Genetics, 192(4), 1447-1454. https://doi.org/10.1534/genetics.112.145078
Nossal, R. J., & Lecar, H. (1991). Molecular and cell biophysics. Addison-Wesley Pub. Co., the Advanced Book Program. https://cir.nii.ac.jp/crid/1130000798357156864
Olson, B. J., Oberholzer, M., Li, Y., Zones, J. M., Kohli, H. S., Bisova, K., Fang, S. C., Meisenhelder, J., Hunter, T., & Umen, J. G. (2010). Regulation of the Chlamydomonas cell cycle by a stable, chromatin-associated retinoblastoma tumor suppressor complex. Plant Cell, 22(10), 3331-3347. https://doi.org/10.1105/tpc.110.076067
Rochaix, J. D. (2013). Chlamydomonas reinhardtii. In S. Maloy & K. Hughes (Eds.), Brenner’s Encyclopedia of Genetics (Second Edition) (pp. 521-524). Academic Press. https://doi.org/https://doi.org/10.1016/B978-0-12-374984-0.00230-8
Seidenberg, A. (1988). On the Volume of a Sphere. Archive for History of Exact Sciences, 39(2), 97-119. http://www.jstor.org/stable/41133846
Sodeinde, O. A., & Kindle, K. L. (1993). Homologous recombination in the nuclear genome of Chlamydomonas reinhardtii. Proceedings of the National Academy of Sciences, 90(19), 9199-9203. https://doi.org/doi:10.1073/pnas.90.19.9199
Tuxhorn, J., Daise, T., & Dentler, W. L. (1998). Regulation of flagellar length in Chlamydomonas [Article]. Cell Motility and the Cytoskeleton, 40(2), 133-146. https://doi.org/10.1002/(SICI)1097-0169(1998)40:2<133::AID-CM3>3.0.CO;2-G
Umen, J. G. (2005). The elusive sizer. Curr Opin Cell Biol, 17(4), 435-441. https://doi.org/10.1016/j.ceb.2005.06.001
Verde, F., Dogterom, M., Stelzer, E., Karsenti, E., & Leibler, S. (1992). Control of microtubule dynamics and length by cyclin A- and cyclin B-dependent kinases in Xenopus egg extracts. The Journal of cell biology, 118(5), 1097–1108. https://doi.org/10.1083/jcb.118.5.1097
Vilfan, A., & Jülicher, F. (2006). Hydrodynamic flow patterns and synchronization of beating cilia. Physical Review Letters, 96(5), 058102.
Wemmer, K. A., & Marshall, W. F. (2007). Flagellar Length Control in Chlamydomonas—A Paradigm for Organelle Size Regulation. In International Review of Cytology (Vol. 260, pp. 175-212). Academic Press. https://doi.org/https://doi.org/10.1016/S0074-7696(06)60004-1
Wheatley, D. N., & Bowser, S. S. (2000). Length control of primary cilia: Analysis of monociliate and multiciliate PtK1 cells [Article]. Biology of the Cell, 92(8-9), 573-582. https://doi.org/10.1016/S0248-4900(00)01108-4
Yang, L., Chen, J., Qin, S., Zeng, M., Jiang, Y., Hu, L., Xiao, P., Hao, W., Hu, Z., Lei, A., & Wang, J. (2018). Growth and lipid accumulation by different nutrients in the microalga Chlamydomonas reinhardtii. Biotechnol Biofuels, 11, 40. https://doi.org/10.1186/s13068-018-1041-z