Applications of Newtonian Mechanics in the Animal Molting Process
Sidrah Alousi-Jones, Le Chen, Léanne Gauthier, Haley Janvrin
Abstract
Molting or ecdysis is the intricate yet routine biological process through which the external layer is shed and replaced. Molting is necessary as it allows organisms to grow at a healthy rate, however it is a very risky process that often leaves the animal vulnerable and exposed for the duration of the molt. This report explains the molting process in relation to Newtonian mechanics, outlining how the three animals rely on these basic principles of physics to overcome the challenges associated with molting and safely reach adulthood. The Californian spiny lobster applies principles of friction to create a rasping sound during the vulnerable phases of its molt to ward off predators. The Harris's Hawk's gliding performance is directly related to the aerodynamic force and thus lift to drag ratio. As the wing area and span change throughout the hawk's molt, its ability to glide decreases then renews as feathers are replenished. Finally, the mechanical properties of the desert locust's exoskeleton change to facilitate the molting process; namely, the new cuticle alters its stiffness and elasticity to either prevent or encourage deformation at various points in the molt cycle, in accordance with Newton's third law. Newtonian mechanics allow living organisms to manage the necessary risk of moulting in order to achieve successful adulthood.
Introduction
Molting is the process through which hair, horns, feathers, shell or an outer layer are shed periodically. It can also be referred to as ecdysis (Merriam-Webster, n.d.). This process can be critical for growth, temperature regulation and can enable metamorphosis in certain organisms. Newtonian mechanics can be observed, and its principles applied throughout the molting process. Firstly, Newton's laws and their applications are discussed in the following paper. Then, the molting of three distinct animals is presented and links are drawn between each animal's molting and mechanics. This analysis not only highlights the presence of Newtonian law in the biological processes, but it also provides points of comparison and contrast between biomechanics and engineered systems and engineering models.
Applications of Newton's laws
Newtonian law is foundational to the world of classical mechanics. Isaac Newton (1642-1727) established three notable laws which offered insight into the characteristics of motion and systems. Newton's first law of inertia states that “a body at rest tends to stay at rest, whereas a body in motion tends to stay in motion” (Urone, 2021d). In other words, “a body at rest or in motion at constant velocity remains in that state unless acted upon by an external force” (Urone, 2021d). His second law is directly related to his first. It describes the relationship between a force applied on an object and its subsequent change in motion. “It states that F = ma” (Urone, 2021d). Finally, his third deals with matters of symmetry. It explains force pair interactions: one body cannot apply a force on another without experiencing an equal and opposite force to the one it applies (Urone, 2021d). There are several forces that provide further applications for Newtonian law. Friction, gliding as well as deformation are examples of such forces (Urone, 2021d). Friction is “a force which opposes the motion or attempted motion between two systems” (Urone, 2012c). The concept of friction is still not fully understood, as will be further explored in the molting of the California spiny lobster. However, understanding Newtonian mechanics allows us to describe friction's characteristics and behaviour. For example, due to Newton's first law of motion, it is possible to understand why an object sliding across a rough surface slows down due to frictional force (Urone, 2012c). As for drag forces, they can be felt, for example, when one runs their hand through a pool of water. Like friction, it opposes the motion of an object. Lift is a force which contrasts drag. The motion of a gliding flying object, be it a bird or a plane, is well described by the law of inertia. When equilibrium exists between the forces of weight, lift and drag, the object flies at constant velocity (Urone, 2021a). The notions of drag and gliding can be analyzed when referring to the molting of Harris' Hawk. In the case of deformation, Newton's laws are not only applied to an object's motion, but also to its shape. “A change in shape due to the application of a force is called deformation” (Urone, 2012b). By Newton's third law, “the deformation of a body due to a force creates a force in the opposite direction called the restoring force. When the restoring force is proportional to displacement, Hooke's law states that F = kΔl” (Urone, 2012b). Objects are said to be stiffer than others when they deform less for a given force applied (Urone, 2012b). Elasticity and stiffness are concepts which will be applied to better understand the mechanical properties of the cuticle of the desert locust.
The vulnerability of the California spiny lobster during molting
The molting period and process
The molting of the California spiny lobster (Panulirus interruptus) is unlike most other arthropods (Fig.1). It is particularly noteworthy because of the way in which it makes use of physics as a means of protection during the most vulnerable time in its molt cycle. Once hatched, spiny lobster larvae undergo intense growth and therefore, molt 12 times in this first period of their lives. At adulthood, the time between consecutive molts increases; adult spiny lobsters molt annually (Bodkin & Brown, 1992).
Before its exoskeleton is shed, the California spiny lobster begins to form a new, soft shell underneath the older shell. When the lobster removes it shell during ecdysis, it begins by rupturing the thoracic cavity of the exoskeleton, so that the eyes and antennae first emerge. The spiny lobster then uses peristaltic contractions to free its abdomen from the exoskeleton. A writhing motion is employed to dislodge the cephalothorax. The end of the process coincides with a forceful tail flip (Lipcius & Hernkind, 1982). Before its shell mineralizes and hardens, the lobster will begin to increase its water uptake in to expand its soft shell (Bodkin & Brown, 1992) (refer to Cabrillo Marine Aquarium, 2020 in Appendix).

Sound produced by stick and slip friction
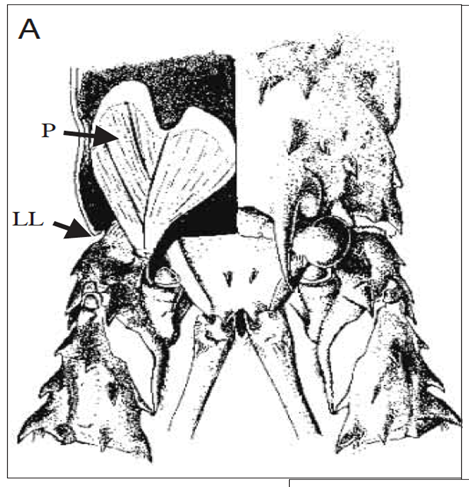
Without its hard shell, the lobster is much more vulnerable to injury and to predators. To protect themselves, lobsters produce rasping noises which are intended to fend off predators. The rasping is made up of a sequence of sound pulses (Patek, 2001) (refer to California Academy of Sciences,2015 in Appendix). Lobsters are not unique in their choice of method of protection. Many arthropods create deterring rasping sounds by rubbing a rough or bumpy area of their exoskeleton on a hard surface. In other words, a typical arthropod will rub a rigid pick (plectrum) over macroscopic ridges (file). This is comparable to running a stick (plectrum) over a washboard (file). However, before a lobster's exoskeleton has hardened during the molt cycle, it is unequipped to perform the washboard technique. Instead, it uses stick and slip friction to produces its cries (Patek, 2002). It is important to note that, in the spiny lobster's case, its plectrum is flexible and its file, macroscopically ridge-less. To produce its sound, the lobster rubs the soft plectrum situated on the end of each antenna and over the file, which is located just below the eye (Fig. 2). The plectrum has large ridges composed of soft tissue (0.1μm width) and the file is made up of rigid microscopic shingles (0.1μm in width) (Fig. 3). Lobsters produce their sound by rubbing their antennas in a posteriorly directed motion over the file (Patek & Baio, 2007) (refer to PatekLab, 2009 in Appendix.)

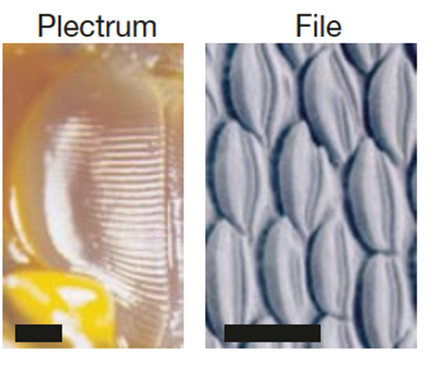
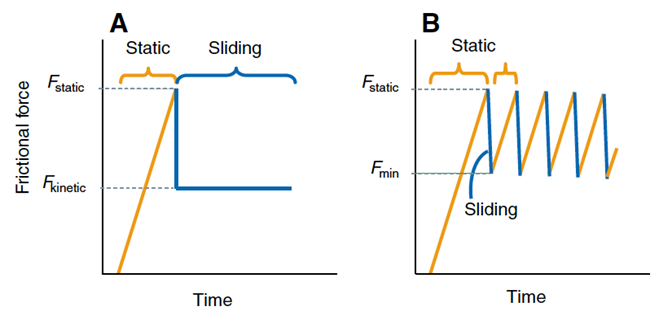
It is the friction between plectrum and file which enables the lobster to rasp. Newtonian friction principles are often applied to cases of steady-sliding objects; a mass sliding down a ramp, a hockey puck sent across the ice. However, frictional characteristics of the lobster's mechanism are comparable to that of a bowed instrument such as a violin. To cause a violin string to vibrate, the bow must stick, because of static friction and then slip over the string, because of to kinetic friction. Stick and slip friction is often modelled by a mass and spring system (Patek, 2001). A mass is attached to a spring and resting on a surface and when the block is in its sticking phase: F ≤ us. Once the applied spring force is greater than the force of static friction, the block begins to slide, and kinetic friction then comes into play. The block's motion is opposed by a changing frictional force. As long as the force of static friction is greater than that of kinetic friction, the block accelerates. The spring will extend beyond its equilibrium length. The mass then decelerates until it fully stops at which point static friction will once again act on the system. The cycle then starts over. The complication of this is that, as the velocity of the mass' motion changes, so does the kinetic friction (Berman et al., 1996) (Fig. 4). It is debated that it is not even possible to measure kinetic friction because of the fluctuations in velocity (Patek & Baio, 2007) (Fig. 5).
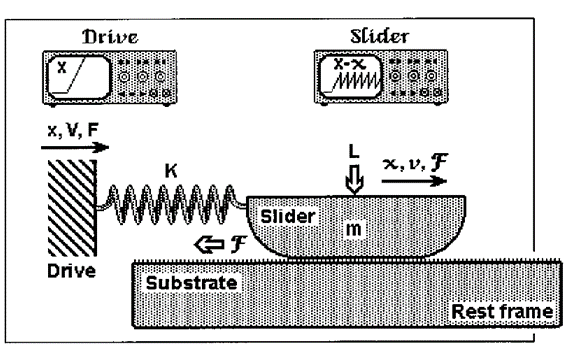
The lobster's use of the stick and slip mechanism is better described by a system of a mass linked to two springs (Fig. 6). The same Newtonian principles apply, only an extra spring is introduced. Static friction is responsible for the sticking between the two surfaces here as well. As the plectrum, represented by the two springs, extends and compresses on either end, static friction is exceeded and sliding occurs. Sound is then produced. It is the softness and elasticity of the plectrum tissue which is responsible for the storing and releasing of energy (Patek & Baio, 2007).
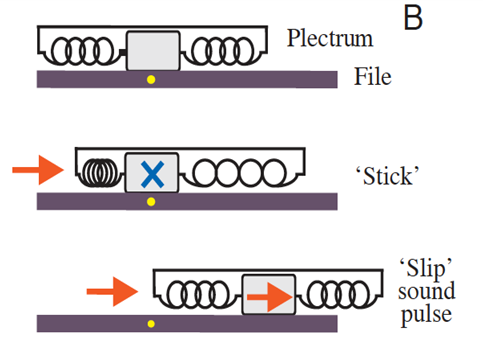
It has been observed that lobsters only produced sound during the slipping movement and that every slip coincides with a pulse (Patek, 2002) (Fig. 7). The particularities of the mechanism and consequently of the sound produced are dependent on a variety of variables such as elasticity, velocity, and normal force (Patek & Baio, 2007). To better visualize this, one can refer to how a violin player controls their instrument's sound. By pressing on their bow, they increase the normal force and consequentially, the force of static friction. The bow's material composition also effects the sound produced. In Patek & Baio's 2007 study, the velocity at which the lobsters moved their antennae over the file was found to be positively correlated with the amplitude of the sound they produced. Therefore, it has been proposed that the lobsters can control the sound they produce through velocity and normal force. When examining lobster morphology and more specifically, that of the plectrum, it is possible to see that the lobster moves its plectrum by contracting its promoter muscle. This muscle runs from the antennae to the dorsal cephalothorax. During sound production, activity was observed not only in the promoter muscle, but also in the lateral levator. This muscle extends from the antennae to the lateral cephalothorax. Therefore, the variation in lobster sound is likely the result of promoter and lateral levator muscle control which allow the lobster more quickly or more forcefully (Patek, 2002) (Fig 8).

Flight of Harris's Hawk during molting
Harris's Hawk morphology and molting
Harris's hawks are medium-large raptors with long legs and tails. They range from 46 to 59 cm in length, 515 to 880 g in weight, and have a wingspan of 103 to 119 cm. Harris's hawk are dark brown in general. They are soaring birds that perch on poles, posts, or other places that give them a good view of the surroundings (All About Birds, n.d.). Like many other birds, Harris's hawks undergo the process of molting, that replaces their old feathers with new ones.
This section will present how molting affect the gliding performance of a Harris' Hawk. However, this section will first discuss the parts of a bird that predominantly determine its flying performance: the flight feathers (Fig. 9).
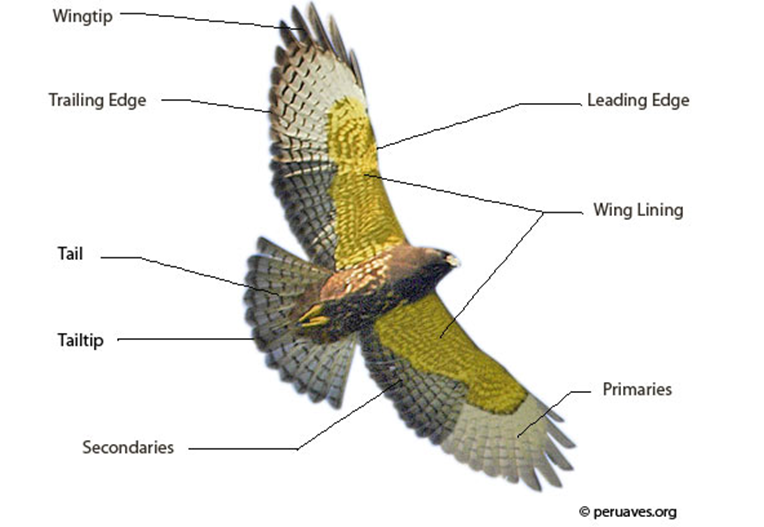
The flight feathers of a bird can be classified as wing feathers and tail feathers. Wing feathers, also known as remiges, are made up of primary, secondary and tertiary feathers. Primary feathers are the largest feathers among wing feathers. They are the longest and the farthest away from the body, attached to the wing on the “hand” of the bird. Most birds have 10 primary feathers on each wing (Science Learning Hub, 2011). Conventionally, the 10 primary feathers are denoted from P1 (nearest the secondary feathers) to P10 (on the leading edge of the wing) (Fig. 10) (Tucker, 1991). Secondary feathers are closer to a bird's body that make up the “arm” of the wing. The number of secondary feathers is different between species. Tertiary feathers attach to the “upper arm” of the bird that are the closest to the body. Tertiary feathers do not have equal significance for flight as the primary and secondary feathers (Science Learning Hub, 2011).

Flight and gliding at equilibrium
A bird gliding at equilibrium moves at constant air speed V along a path at an angle θ below the horizontal axis. Force and velocity vectors during equilibrium gliding are shown in Fig. 11 (Tucker & Heine, 1990).

Sinking speed (Vs), pointing vertically downwards, is given by:
Vs = V sin θ (1)
Weight (W), pointing vertically downwards, is given by the product of mass and gravitational acceleration:
W = mg (2)
The aerodynamic force exerted on the bird is equal in magnitude to the weight (W) and opposite in direction, that is, vertically upwards (Tucker, 1991). Thus, the force has two components: lift (L), perpendicular to the flight path, is given by:
L = W cos θ = mg cos θ (3)
and drag (D), parallel to the flight path, is given by:
D = W sin θ = mg sin θ (4)
Small angle approximation can be made because θ is normally less than 10° when birds are gliding at maximum performance (Tucker, 1991), therefore, cos θ is about 1. With this approximation, equation (3) can be rewritten as:
L = mg
Then
{L\over D} = {mg\over mg sin θ} = {1\over sin θ}Rewrite
{1\over sin θ} = {V\over VS}Thus
Smaller sinking speed (VS) means that the bird decreases in height at a smaller rate and thus travels a longer distance before landing on the ground, that is, the better gliding performance (Tucker, 1991). Equation (5) shows that if the sinking speed (VS) decreases, the ratio of lift to drag (L/D) increases. Therefore, the ratio of lift to drag (L/D) is a measure of the bird's gliding performance: the larger the L/D value is, the better the bird's gliding performance is (Tucker, 1991).
{L\over D} = {V\over VS} (5)The gliding performance of a male Harris's hawk was studied by Tucker & Heine (1990) during its molting period between June 15th and December 4th, 1989. During its molting period, the large primary feathers shed were collected by Tucker and were identified as primaries 5-9. As forementioned, the number of primary feathers is the location of certain primary feather on the wing. It was found by Tucker that: the hawk shed primaries 5-8 on each wing between 15 June and 21 July; most of the new primary feathers grew in and were as long as the original feathers on July 21; however, primary 6 was still shorter while a significant gap between primaries 5 and 7 was noticed; moreover, the shedding of primary 9 also left a gap, however it was narrower than the shedding of primary 6; a secondary feather occasionally shed and the new one was a little shorter than its final length (Tucker, 1991). The tail feather length remained unchanged while old feathers were gradually replaced by new ones (Tucker, 1991). The hawk's gliding performance was continuously studied throughout its molting period by measuring the hawk's maximum L/D values. The feather conditions and maximum L/D values from pre- to postmolt are shown in Figure 12 and Table 1.
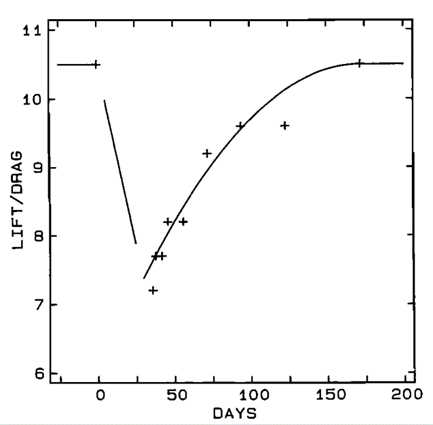

It has been observed that the hawk's gliding performance was degraded during its molting period. This can correlate with “(1) the appearance of gaps in the wing tips caused by missing primary feathers, and (2) the temporary shortening of the primary feathers until the new primary feathers reach their final length” (Tucker, 1991). As a result, the wing area and span, as well as the shape of the wing tips of the hawk, were no longer the same during its molting period (Tucker, 1991). Its gliding performance was at the weakest point when it lost its primaries 5-8 and had gaps in wing tips. As new feathers grew in, its gliding performance continuously improved, and it returned to a L/D value of 10.5 when new feathers were complete. However, Tucker also claims that the changes in wing area and span cannot solely account for all the reduction in L/D values. Another factor called induced drag can also account for the reduction in L/D values (Tucker, 1991), but this concept will not be detailed further in this section.
The mechanical properties of the desert locust cuticle during molting
The ecdysis process for insects
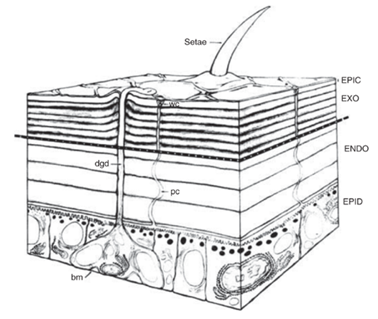
In insects, the molting process is known as ecdysis, which is characterized by the shedding of the cuticle, the insect's exoskeleton consisting of the epicuticle, exocuticle, and endocuticle (Fig. 13). All three layers of the cuticle lie above the epidermis, a single cell layer which secretes chitin microfibrils and proteins leading to the formation of a new cuticle via self-assembly during the intermolt period (Riddiford, 2009). The old cuticle remains unaffected during this process to preserve the insect's capacity to move. At the onset of ecdysis, a molting gel containing inactive proteolytic and chitinolytic enzymes is secreted between the old cuticle and the epidermis border in preparation for the shedding of the old exoskeleton (Riddiford, 2009). Shortly before ecdysis behaviour commences, these enzymes are activated by specific proteases secreted into the molting gel, which rid the proteolytic and chitinolytic enzymes of their inactive regions. The activated chitinases and proteases then break down the old endocuticle into its precursor components, namely amino acids and sugars, which are resorbed along with the molting fluid to be recycled during subsequent molting cycles (Riddiford, 2009). The molting cycle then enters the preecdysis period, during which a combination of coordinated movements and peristaltic waves allow the detachment of the muscles from the old cuticle as well as the rupture of the exoskeleton to be shed (Riddiford, 2009). Upon completion of this process, the insect inflates its abdomen and trachea to expand the new cuticle. Once the suitable size is attained, hardening and darkening of the cuticle take place, a process known as sclerotization.
Sclerotization and mechanical properties
Sclerotization is a stabilization process during which the exocuticle is hardened by the crosslinking of the proteins together as well as with chitin via the cross-linking agents N-acetyldopamine and N-β-alanyldopamine, two dopamine derivatives incorporated into the cuticular matrix (Andersen, 2012). The degree of sclerotization varies within distinct cuticular regions; some regions are more flexible and supple, whereas other regions exhibit significant stiffness. In fact, sclerotization is identified as one of the primary determinants of the mechanical properties exhibited by the cuticular regions. More specifically, sclerotization increases the compressive strength, the modulus and the flexion rigidity of the cuticle to a greater degree than the tensile properties (Jensen & Weis-Fogh, 1962). Factors such as cuticular thickness, relative amounts of chitin and proteins, chitin architecture, protein composition, water content, and intracuticular pH also impact the physical properties of the cuticle to a lesser extent (Andersen, 2012). Presumably, the degree of stiffness imparted to each cuticular region is determined by the forces to which it is exposed and by the function it fulfills. For instance, regions involved in the locomotion of the insect, such as the arthrodial membranes, exhibit significant flexibility while wing material show a precise balance of stiffness and flexibility for optimal flight (Andersen, 2012).
The sclerotization process taking place at the end of the molting cycle is not the only period during which variations in the mechanical properties are observed within the cuticle. In fact, precise changes in the cuticle's stiffness and elasticity are crucial for the completion of the various molting periods. This can be exemplified and quantified by the case of Schistocerca gregaria, the desert locust (Fig. 14).

The case of the desert locust (Schistocerca gregaria)
The first observation concerning the mechanical properties of the desert locust's cuticle is the change in its elastic behaviour in the course of the ecdysis process. Jensen & Weis-Fogh (1962) report that stretching the cuticle of an adult locust results in brief extension, consistent with elastic behaviour. However, in order to allow for expansion of the new cuticle following the shedding of the previous exoskeleton, cuticles taken from locusts during ecdysis exhibit viscoelastic behaviour; the cuticle keeps elongating as long as a longitudinal force is maintained (Elliott, 1981). Shortly after the suitable size is attained in the ecdysis process, before sclerotization occurs, elastic properties of the cuticle are recovered. At this stage, Elliott reports a coefficient of elasticity E estimated to be 0.14 GNm-2, obtained using the following equation:
E = S{l\over A}where S is the stiffness, l is the length of the locust and A, its cross-sectional area. This value later reaches 9 GNm-2 once sclerotization is completed and the cuticle is fully stabilized (Elliott, 1981).
Key variations in the cuticle stiffness are also observed throughout the molting cycle of Schistocerca. A significant decrease in cuticular stiffness is observed in the early stages of ecdysis leading to the rupture of the old cuticle. The stiffness of the unfolded wing cuticle drops from 14 Nm-1 to 3.2 Nm-1 at the time of emergence (Elliott, 1981). This softening of the cuticle is of particular importance, as it promotes emergence by facilitating the locust's extrication from the old cuticle while also allowing some early cuticle expansion taking place during the emergence phase. An increase in cuticular stiffness is subsequently observed upon the emergence of the metathoracic legs, before the expansional stage (Elliott, 1981). This allows locomotion shortly after the locust's extrication from its old exoskeleton. Without sufficient stiffness in the leg region of the cuticle, Schistocerca is unable to walk; increased stiffness prevents the deformation and the buckling of the legs. At the onset of the expansional period, a second softening of the cuticle is observed as the stiffness measured for the unfolded wing cuticle drops to 1.9 Nm-1, as reported by Elliott (1981). The variations in cuticular stiffness can be observed on Fig. 15, which illustrates the first drop in stiffness, the increase in stiffness that follows at the emergence of the metathoracic legs (beginning of stage 4), and the second softening that ensues.
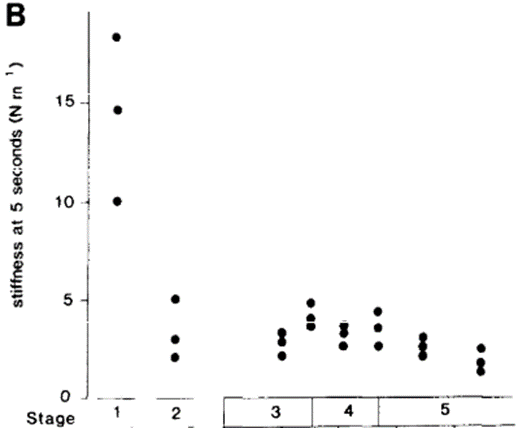
The second decrease in stiffness allows for further expansion of the cuticle, until the sclerotization process begins and the structure is stabilized into its final shape. At this stage, a final increase in stiffness is measured. Elliott states that the stiffness of the expanded wing cuticle is roughly multiplied by 92 in the span of 45 minutes following the onset of sclerotization. This is the final stage of ecdysis; Schistocerca is then ready for the subsequent molting cycle.
Conclusion
As shown by the California spiny lobster, the Harris's Hawk, and the desert locust, Newtonian mechanics are the keystone for animals' survival and success in the wild. The California spiny lobster uses stick and slip friction to stay alive, producing sound to threaten predators by rubbing their antennae across the ridges of the file. During the Harris's Hawk's molt, gaps appear between the feathers which increase drag and decrease gliding performance, thus proving the importance of an aerodynamic shape. The desert locust navigates the balance between elasticity and stiffness to shed the old exoskeleton and create a new one that allows for both protection and mobility. Through these three examples, it's clear that Newtonian mechanics play a critical role in biological processes, further demonstrating that problem solving even in nature is truly interdisciplinary.
Appendix
Cabrillo Marine Aquarium. (2020, June 9). California Spiny Lobster Molting [Video]. Youtube. https://www.youtube.com/watch?v=4WCuXCx4oSU
California Academy of Sciences. (2015, April 17). Spiny Lobster Sound File | California Academy of Sciences [Video]. Youtube. https://www.youtube.com/watch?v=7HnwBaYQU38
PatekLab. (2009, September 28). High speed video of a California spiny lobster producing sound [Video]. Youtube. https://www.youtube.com/watch?v=b58OowCXnqc
References
All About Birds. (n.d.). Harris's Hawk Identification. TheCornellLab. Retrieved October 6, 2021, from https://www.allaboutbirds.org/guide/Harriss_Hawk/id
Andersen S. O. (2012). “Cuticular Sclerotization and Tanning,” in Insect Molecular Biology and Biochemistry, L. I. Gilbert, Ed. San Diego: Academic Press, pp. 167-192.
Avian Report. (2021, September 30). Parts of a bird: Flight Feathers. Avian Report. Retrieved October 6, 2021, from https://avianreport.com/bird-flight-tail-feathers/.
Berman, A. D., Ducker, W. A., & Israelachvili, J. N. (1996). Origin and Characterization of Different Stick−Slip Friction Mechanisms. Langmuir, 12(19), 4559–4563. https://doi.org/10.1021/la950896z
Bodkin, J.L. and L. Brown. 1992. Molt frequency and size-class distribution in the California spiny lobster (Panulirus interruptus) as indicated by beach-cast carapaces at San Nicolas Island, California. Calif. Fish and Game 78(4):136-144.
Elliott C. J. H. (1981). “The expansion of Schistocerca gregaria at the imaginal ecdysis: The mechanical properties of the cuticle and the internal pressure,” Journal of Insect Physiology, Article vol. 27, no. 10, pp. 695-704.
Ess, C. (2021, April 13). Pacific spiny lobster: After pandemic low-price worries, this season could reach new highs. National Fisherman. https://www.nationalfisherman.com/west-coast-pacific/pacific-spiny-lobster-after-pandemic-low-price-worries-this-season-could-reach-new-highs
istockphoto. (n.d.). Why sequence desert locust (Schistocerca gregaria)? Joint Genome Institute. Retrieved October 6, 2021, from https://jgi.doe.gov/why-sequence-desert-locust-schistocerca-gregaria/
Jensen M. and Weis-Fogh T. (1962).”Biology and physics of locust flight. V. Strength and elasticity of locust cuticle,” Phil. Trans. R. Soc. Lond. B, vol. 245, no. 721, pp. 137-169.
Lipcius, R. N., & Herrnkind, W. F. (1982). Molt cycle alterations in behavior, feeding and diel rhythms of a decapod crustacean, the spiny lobster Panulirus argus. Marine Biology, 68(3), 241–252. https://doi.org/10.1007/bf00409591
Merriam-Webster. (n.d.). Molt. In Merriam-Webster.com dictionary. Retrieved July 26, 2022, from https://www.merriam-webster.com/dictionary/molt
Patek, S. N. (2001). Spiny lobsters stick and slip to make sound. Nature, 411(6834), 153–154. https://doi.org/10.1038/35075656
Patek, S. N. (2002). Squeaking with a sliding joint: mechanics and motor control of sound production in palinurid lobsters. Journal of Experimental Biology, 205(16), 2375–2385. https://doi.org/10.1242/jeb.205.16.2375
Patek, S. N., & Baio, J. E. (2007). The acoustic mechanics of stick–slip friction in the California spiny lobster (Panulirus interruptus). Journal of Experimental Biology, 210(20), 3538–3546. https://doi.org/10.1242/jeb.009084
Persson, B. N. J. (2000). Sliding Friction: Physical Principles and Applications (NanoScience and Technology) (2nd ed.). Springer.
Riddiford L. M. (2009). “Molting,” in Encyclopedia of Insects (Second Edition), V. H. Resh and R. T. Cardé, Eds. San Diego: Academic Press, pp. 649-654.
Tucker, V. A., & Heine, C. (1990). Aerodynamics of Gliding Flight in a Harris' Hawk, Parabuteo unicinctus. Journal of Experimental Biology, 149(1), 469-489. https://doi.org/10.1242/jeb.149.1.469
Tucker, V. A. (1991). The effect of molting on the gliding performance of a Harris' Hawk (Parabuteo unicinctus). The Auk, 108(1), 108-113. https://doi.org/10.1093/auk/108.1.108
Urone, P. P. (2012a, January 23). Drag Forces – College Physics. Pressbooks. https://opentextbc.ca/openstaxcollegephysics/chapter/drag-forces/
Urone, P. P. (2012b, January 23). Elasticity: Stress and Strain – College Physics. Pressbooks. https://opentextbc.ca/openstaxcollegephysics/chapter/elasticity-stress-and-strain/
Urone, P. P. (2012c, January 23). Friction – College Physics. Pressbooks. https://opentextbc.ca/openstaxcollegephysics/chapter/friction/
Urone, P. P. (2012d, January 23). Further Applications of Newton's Laws of Motion – College Physics. Pressbooks. https://opentextbc.ca/openstaxcollegephysics/chapter/further-applications-of-newtons-laws-of-motion/
Science Learning Hub. (2011, September 16). Feathers and flight. https://www.sciencelearn.org.nz/resources/308-feathers-and-flight